Question Number 77539 by TawaTawa last updated on 07/Jan/20

Commented by TawaTawa last updated on 07/Jan/20
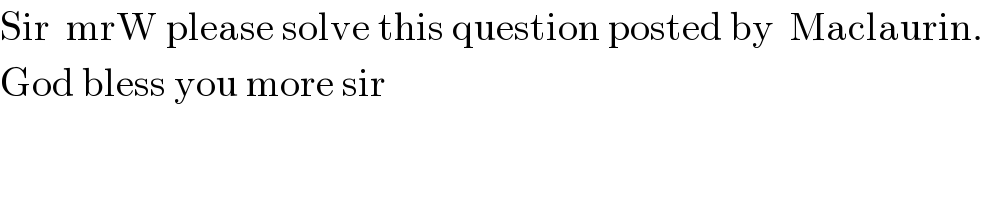
$$\mathrm{Sir}\:\:\mathrm{mrW}\:\mathrm{please}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{question}\:\mathrm{posted}\:\mathrm{by}\:\:\mathrm{Maclaurin}. \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{more}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 07/Jan/20
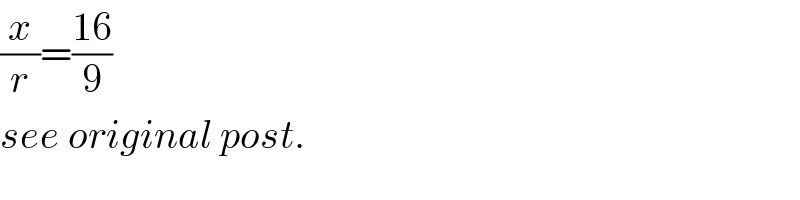
$$\frac{{x}}{{r}}=\frac{\mathrm{16}}{\mathrm{9}} \\ $$$${see}\:{original}\:{post}. \\ $$
Commented by TawaTawa last updated on 07/Jan/20
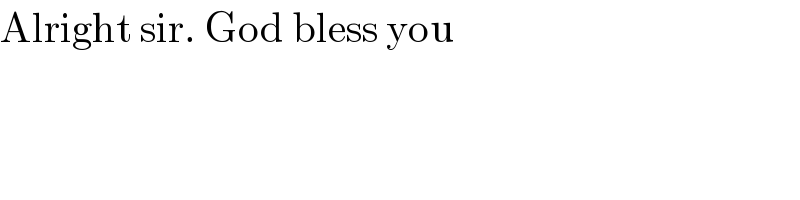
$$\mathrm{Alright}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$
Commented by mr W last updated on 08/Jan/20

Commented by mr W last updated on 08/Jan/20
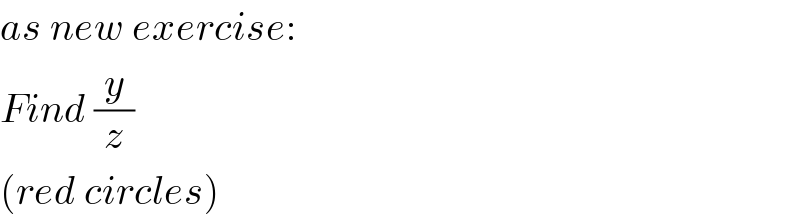
$${as}\:{new}\:{exercise}: \\ $$$${Find}\:\frac{{y}}{{z}} \\ $$$$\left({red}\:{circles}\right) \\ $$
Commented by TawaTawa last updated on 08/Jan/20
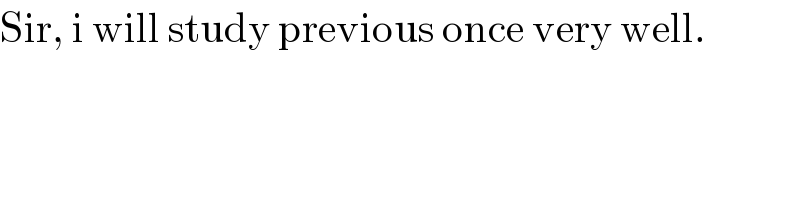
$$\mathrm{Sir},\:\mathrm{i}\:\mathrm{will}\:\mathrm{study}\:\mathrm{previous}\:\mathrm{once}\:\mathrm{very}\:\mathrm{well}. \\ $$
Commented by TawaTawa last updated on 09/Jan/20

$$\mathrm{I}\:\mathrm{was}\:\mathrm{busy}\:\mathrm{with}\:\mathrm{the}\:\mathrm{Lambert}\:\mathrm{W}\:\mathrm{functions}.\:\mathrm{Now}\:\mathrm{am} \\ $$$$\mathrm{through}\:\mathrm{with}\:\mathrm{it}.\:\mathrm{I}\:\mathrm{would}\:\mathrm{like}\:\mathrm{to}\:\mathrm{test}\:\mathrm{myself}\:\mathrm{if}\:\mathrm{i}\:\mathrm{have}\:\mathrm{truly} \\ $$$$\mathrm{understood}\:\mathrm{it}\:\mathrm{by}\:\mathrm{giving}\:\mathrm{me}\:\mathrm{question}\:\mathrm{on}\:\mathrm{it}. \\ $$
Commented by TawaTawa last updated on 09/Jan/20
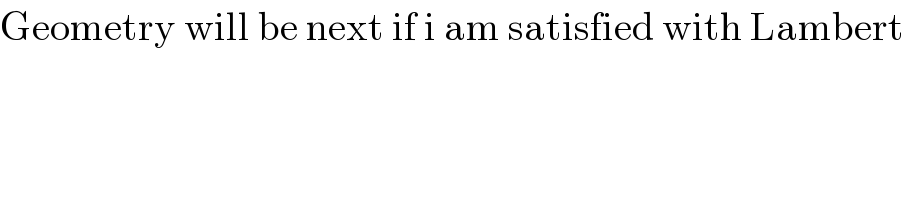
$$\mathrm{Geometry}\:\mathrm{will}\:\mathrm{be}\:\mathrm{next}\:\mathrm{if}\:\mathrm{i}\:\mathrm{am}\:\mathrm{satisfied}\:\mathrm{with}\:\mathrm{Lambert} \\ $$
Commented by TawaTawa last updated on 09/Jan/20
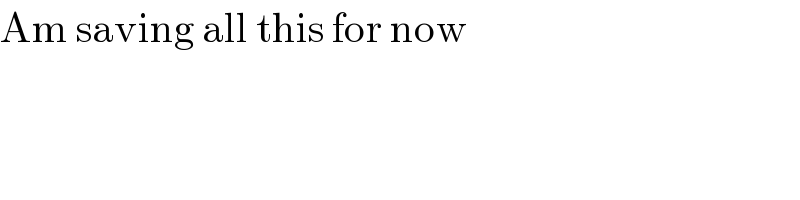
$$\mathrm{Am}\:\mathrm{saving}\:\mathrm{all}\:\mathrm{this}\:\mathrm{for}\:\mathrm{now} \\ $$
Commented by mr W last updated on 09/Jan/20

$${i}\:{think}\:{you}\:{should}\:{have}\:{lernt}\:{all} \\ $$$${things}\:{about}\:{Lambert}\:{function}.\:{just} \\ $$$${apply}\:{that}!\:{just}\:{study}\:{the}\:{existing} \\ $$$${questions}\:{in}\:{forum}!\:{i}\:{can}'{t}\:{give}\:{you} \\ $$$${any}\:{new}\:{questions}\:{or}\:{i}\:{don}'{t}\:{want}\:{to} \\ $$$${do}\:{this}. \\ $$
Commented by TawaTawa last updated on 09/Jan/20

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{will}\:\mathrm{do}\:\mathrm{that}. \\ $$
