Question Number 77593 by BK last updated on 08/Jan/20
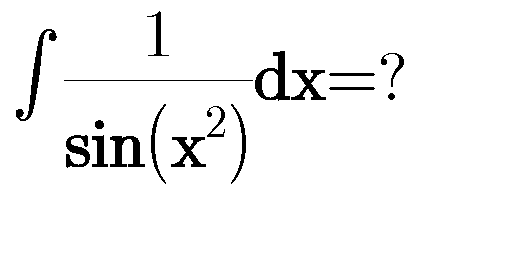
Commented by $@ty@m123 last updated on 08/Jan/20
$${The}\:{repeatation}\:{of}\:{this}\:{question}\: \\ $$$${is}\:{sufficient}\:{to}\:{prove}\:{that}\:{Mr}.\:{BK} \\ $$$${is}\:{none}\:{other}\:{than}… \\ $$
Commented by BK last updated on 08/Jan/20

$$????\:\::\left(\right. \\ $$
Commented by mr W last updated on 08/Jan/20
$${clear}\:{things}\:{need}\:{no}\:{proof}! \\ $$
Commented by MJS last updated on 08/Jan/20

$$\mathrm{Sir}\:\mathrm{BK},\:\mathrm{why}\:\mathrm{do}\:\mathrm{you}\:\mathrm{ask}\:\mathrm{this}\:\mathrm{question}? \\ $$$$\int\frac{{dx}}{\mathrm{sin}\:{x}^{\mathrm{2}} }=? \\ $$$$\mathrm{do}\:\mathrm{you}\:\mathrm{need}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{for}\:\mathrm{your}\:\mathrm{studies}? \\ $$$$\mathrm{then}\:\mathrm{you}\:\mathrm{must}\:\mathrm{have}\:\mathrm{learned}\:\mathrm{how}\:\mathrm{to}\:\mathrm{solve} \\ $$$$\int\mathrm{sin}\:{x}^{\mathrm{2}} \:{dx}\:\mathrm{first}.\:\mathrm{or}\:\mathrm{are}\:\mathrm{you}\:\mathrm{just}\:\mathrm{interested}\:\mathrm{in} \\ $$$$\mathrm{solving}\:\mathrm{integrals}?\:\mathrm{then}\:\mathrm{you}\:\mathrm{must}\:\mathrm{already} \\ $$$$\mathrm{understand}\:\mathrm{a}\:\mathrm{lot},\:\mathrm{show}\:\mathrm{us}\:\mathrm{how}\:\mathrm{you}\:\mathrm{solve} \\ $$$$\int\frac{{x}}{\mathrm{sin}\:{x}^{\mathrm{2}} }{dx}\:\mathrm{or}\:\int{x}\mathrm{tan}\:{x}^{\mathrm{2}} \:{dx}.\:\mathrm{then}\:\mathrm{it}\:\mathrm{makes}\:\mathrm{sense} \\ $$$$\mathrm{to}\:\mathrm{discuss}\:\mathrm{this}\:\mathrm{given}\:\mathrm{integral}.\:\mathrm{otherwise}\:\mathrm{I} \\ $$$$\mathrm{feel}\:\mathrm{like}\:\mathrm{explaining}\:\mathrm{multiplication}\:\mathrm{to}\:\mathrm{my}\:\mathrm{cat} \\ $$
Commented by BK last updated on 08/Jan/20

$$\mathrm{specifiy}\:\mathrm{the}\:\mathrm{accuracy} \\ $$
Commented by $@ty@m123 last updated on 08/Jan/20

$${Same}\:{as}\:{the}\:{probability}\:{of}\:{drawing} \\ $$$${a}\:{red}\:{ball}\:{from}\:{a}\:{contaioner} \\ $$$${containing}\:{only}\:{red}\:{balls}. \\ $$
Commented by MJS last updated on 08/Jan/20
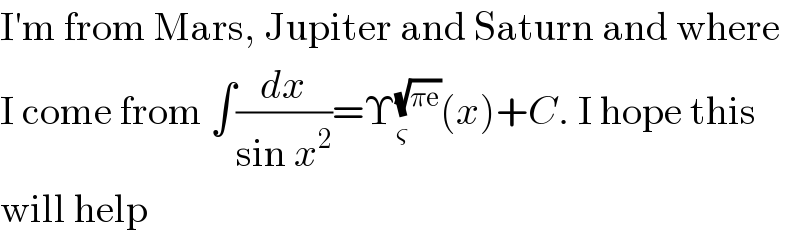
$$\mathrm{I}'\mathrm{m}\:\mathrm{from}\:\mathrm{Mars},\:\mathrm{Jupiter}\:\mathrm{and}\:\mathrm{Saturn}\:\mathrm{and}\:\mathrm{where} \\ $$$$\mathrm{I}\:\mathrm{come}\:\mathrm{from}\:\int\frac{{dx}}{\mathrm{sin}\:{x}^{\mathrm{2}} }=\Upsilon_{\varsigma} ^{\sqrt{\pi\mathrm{e}}} \left({x}\right)+{C}.\:\mathrm{I}\:\mathrm{hope}\:\mathrm{this} \\ $$$$\mathrm{will}\:\mathrm{help} \\ $$
Commented by mr W last updated on 08/Jan/20

$${for}\:{the}\:{case}\:{that}\:{he}\:{tomorrow}\:{posts}\: \\ $$$$\int\frac{{dx}}{\mathrm{sin}\:{x}^{\mathrm{3}} }\:{and}\:{the}\:{day}\:{after}\:{tomorrow} \\ $$$$\int\frac{{dx}}{\mathrm{sin}\:{x}^{\mathrm{4}} }\:{etc}.,\:{you}\:{should}\:{tell}\:{him}\:{the} \\ $$$${extended}\:{Martian}\:{Integral}\:{of}\:{the} \\ $$$${Second}\:{Kind}: \\ $$$$\int\frac{{dx}}{\mathrm{sin}\:{x}^{{n}} }=\Upsilon_{\varsigma} ^{\sqrt{\pi\mathrm{e}}} \left({x}\mid\frac{{n}\pi}{\mathrm{2}}\right)+{C} \\ $$
Commented by MJS last updated on 08/Jan/20
��
Commented by mr W last updated on 08/Jan/20

$${i}\:{guess}\:{you}\:{won}'{t}\:{get}\:{an}\:{answer}\: \\ $$$${from}\:{him},\:{sir}.\:{he}\:{seems}\:{to}\:{be}\:{collecting} \\ $$$${questions}\:{from}\:{all}\:{countries}\:{just}\:{in} \\ $$$${order}\:{to}\:{post}\:{them}\:{here},\:{even}\:{when} \\ $$$${he}\:{doesn}'{t}\:{know}\:{what}\:{or}\:{why}\:{he}\:{asks}. \\ $$
