Question Number 77614 by BK last updated on 08/Jan/20

Commented by BK last updated on 08/Jan/20

$$\mathrm{find}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{A}_{\mathrm{x}} \\ $$
Commented by mr W last updated on 08/Jan/20

$${habla}\:{espa}\overset{\sim} {{n}ol}? \\ $$
Commented by mr W last updated on 08/Jan/20

$${t}\overset{..} {{u}rk}\underset{\varsigma} {{c}e}\:{biliyor}\:{musun}? \\ $$
Commented by mr W last updated on 08/Jan/20

$${both}? \\ $$
Commented by mr W last updated on 08/Jan/20
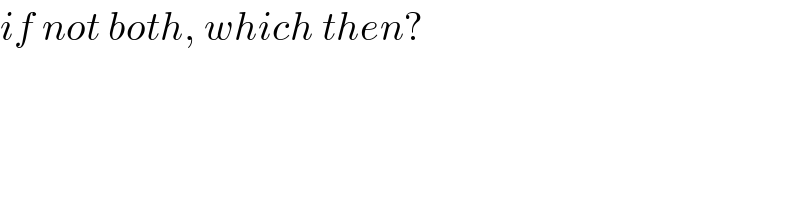
$${if}\:{not}\:{both},\:{which}\:{then}? \\ $$
Commented by BK last updated on 08/Jan/20

$$\mathrm{im}\:\mathrm{from}\:\mathrm{turkey} \\ $$
Answered by mr W last updated on 08/Jan/20

Commented by mr W last updated on 08/Jan/20
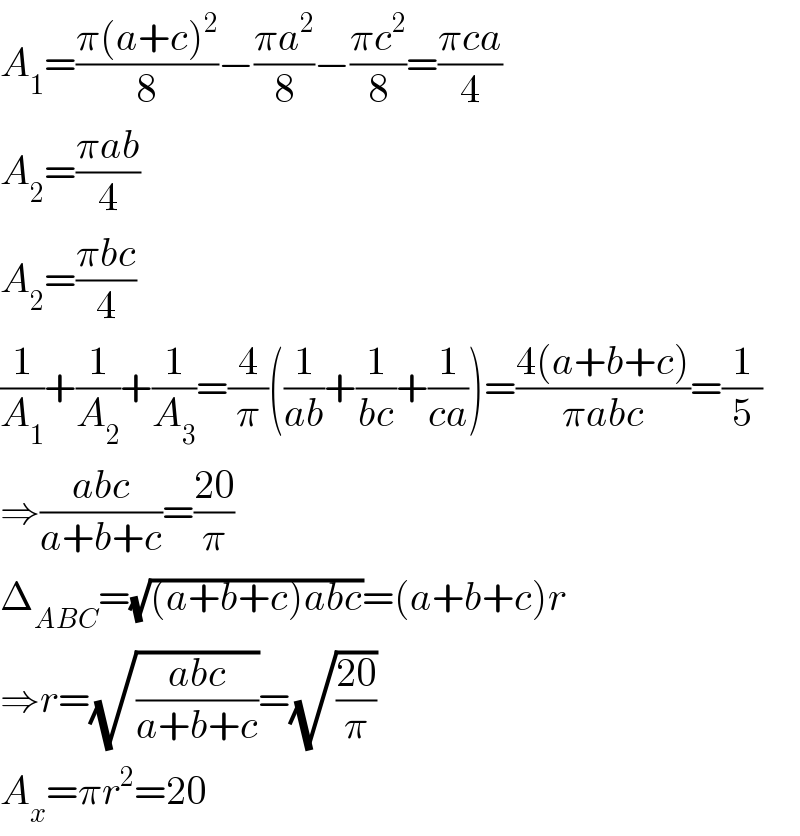
$${A}_{\mathrm{1}} =\frac{\pi\left({a}+{c}\right)^{\mathrm{2}} }{\mathrm{8}}−\frac{\pi{a}^{\mathrm{2}} }{\mathrm{8}}−\frac{\pi{c}^{\mathrm{2}} }{\mathrm{8}}=\frac{\pi{ca}}{\mathrm{4}} \\ $$$${A}_{\mathrm{2}} =\frac{\pi{ab}}{\mathrm{4}} \\ $$$${A}_{\mathrm{2}} =\frac{\pi{bc}}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{{A}_{\mathrm{1}} }+\frac{\mathrm{1}}{{A}_{\mathrm{2}} }+\frac{\mathrm{1}}{{A}_{\mathrm{3}} }=\frac{\mathrm{4}}{\pi}\left(\frac{\mathrm{1}}{{ab}}+\frac{\mathrm{1}}{{bc}}+\frac{\mathrm{1}}{{ca}}\right)=\frac{\mathrm{4}\left({a}+{b}+{c}\right)}{\pi{abc}}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\Rightarrow\frac{{abc}}{{a}+{b}+{c}}=\frac{\mathrm{20}}{\pi} \\ $$$$\Delta_{{ABC}} =\sqrt{\left({a}+{b}+{c}\right){abc}}=\left({a}+{b}+{c}\right){r} \\ $$$$\Rightarrow{r}=\sqrt{\frac{{abc}}{{a}+{b}+{c}}}=\sqrt{\frac{\mathrm{20}}{\pi}} \\ $$$${A}_{{x}} =\pi{r}^{\mathrm{2}} =\mathrm{20} \\ $$
Commented by BK last updated on 08/Jan/20

$$\mathrm{thanks} \\ $$
Commented by Tawa11 last updated on 29/Dec/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
