Question-77681

Question Number 77681 by mr W last updated on 09/Jan/20

Commented by mr W last updated on 09/Jan/20

The radii a, b, c are given. 1. Find radius R of the circumcircle 2. Find radius d of the fourth circle

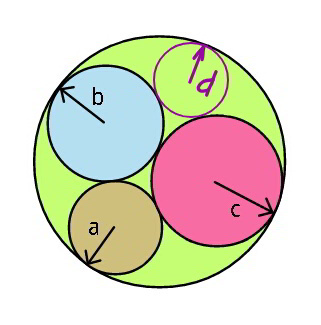
$${The}\:{radii}\:\boldsymbol{{a}},\:\boldsymbol{{b}},\:\boldsymbol{{c}}\:{are}\:{given}. \\ $$$$\mathrm{1}.\:{Find}\:{radius}\:\boldsymbol{{R}}\:{of}\:{the}\:{circumcircle} \\ $$$$\mathrm{2}.\:{Find}\:{radius}\:\boldsymbol{{d}}\:{of}\:{the}\:{fourth}\:{circle} \\ $$

Commented by MJS last updated on 09/Jan/20

I solved this problem with 3 circles and their circumcircle some time ago, do you know the number of that question? there are 4 cases depending on the values of a, b & c, there′s always an incircle but the circumcircle might degenerate to a line or an excircle...

$$\mathrm{I}\:\mathrm{solved}\:\mathrm{this}\:\mathrm{problem}\:\mathrm{with}\:\mathrm{3}\:\mathrm{circles}\:\mathrm{and}\:\mathrm{their} \\ $$$$\mathrm{circumcircle}\:\mathrm{some}\:\mathrm{time}\:\mathrm{ago},\:\mathrm{do}\:\mathrm{you}\:\mathrm{know}\:\mathrm{the} \\ $$$$\mathrm{number}\:\mathrm{of}\:\mathrm{that}\:\mathrm{question}? \\ $$$$\mathrm{there}\:\mathrm{are}\:\mathrm{4}\:\mathrm{cases}\:\mathrm{depending}\:\mathrm{on}\:\mathrm{the}\:\mathrm{values}\:\mathrm{of} \\ $$$${a},\:{b}\:\&\:{c},\:\mathrm{there}'\mathrm{s}\:\mathrm{always}\:\mathrm{an}\:\mathrm{incircle}\:\mathrm{but}\:\mathrm{the} \\ $$$$\mathrm{circumcircle}\:\mathrm{might}\:\mathrm{degenerate}\:\mathrm{to}\:\mathrm{a}\:\mathrm{line}\:\mathrm{or} \\ $$$$\mathrm{an}\:\mathrm{excircle}… \\ $$

Commented by mr W last updated on 09/Jan/20

yes sir, i know your solution in Q37209. thanks! i studied recently problems with circles in triangles and could learn something new which helps greatly for solving this kind of problems. i′ll post something later.

$${yes}\:{sir},\:{i}\:{know}\:{your}\:{solution}\:{in}\:{Q}\mathrm{37209}. \\ $$$${thanks}! \\ $$$${i}\:{studied}\:{recently}\:{problems}\:{with}\: \\ $$$${circles}\:{in}\:{triangles}\:{and}\:{could}\:{learn} \\ $$$${something}\:{new}\:{which}\:{helps}\:{greatly} \\ $$$${for}\:{solving}\:{this}\:{kind}\:{of}\:{problems}. \\ $$$${i}'{ll}\:{post}\:{something}\:{later}. \\ $$

Commented by mr W last updated on 09/Jan/20

For any 4 circles which tangent each other there is a certain quadratic equation which their radii satisfy. this relationship is called Descartes′ Theorem.

$${For}\:{any}\:\mathrm{4}\:{circles}\:{which}\:{tangent}\:{each} \\ $$$${other}\:{there}\:{is}\:{a}\:{certain}\:{quadratic} \\ $$$${equation}\:{which}\:{their}\:{radii}\:{satisfy}. \\ $$$${this}\:{relationship}\:{is}\:{called} \\ $$$$\boldsymbol{{Descartes}}'\:\boldsymbol{{Theorem}}. \\ $$

Commented by mr W last updated on 09/Jan/20

Commented by mr W last updated on 09/Jan/20

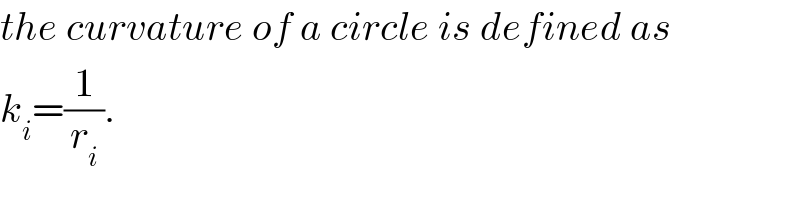
the curvature of a circle is defined as k_i =(1/r_i ).

$${the}\:{curvature}\:{of}\:{a}\:{circle}\:{is}\:{defined}\:{as} \\ $$$${k}_{{i}} =\frac{\mathrm{1}}{{r}_{{i}} }. \\ $$

Commented by jagoll last updated on 09/Jan/20

$${sir}\:{radius}\:{d}\:{unknown}? \\ $$

Commented by mr W last updated on 09/Jan/20

$${radius}\:{d}\:{is}\:{not}\:{independent}.\:{if}\:{a},{b},{c} \\ $$$${are}\:{given},\:{then}\:{d}\:{is}\:{also}\:{given},\:{see} \\ $$$${below}. \\ $$

Commented by ajfour last updated on 30/Dec/21

let center of circumcircle be O. a+c=(R−a)sin α_1 +(R−c)sin β_2 c+b=(R−c)sin β_1 +(R−b)sin γ_2 b+a=(R−b)sin γ_1 +(R−a)sin α_2 ((R−a)/(sin β_1 ))=((R−c)/(sin α_2 ))=((a+c)/(sin (α_2 +β_1 )))=2r and so on... r being radius of circle through centers of circles A, B,C. adding 2(a+b+c)=Σ(R−a)(sin α_1 +sin α_2 ) =Σ(R−a)(((R−b)/(2r))+((R−c)/(2r))) ⇒ 2(a+b+c)=Σ[(((R−a)(2R−b−c))/(2r))] ⇒ 4r(a+b+c) =6R^2 −4R(a+b+c)+2(ab+bc+ca) but if a+b+c=2s ⇒8rs=6R^2 −8Rs+4s^2 −(a^2 +b^2 +c^2 ) .....(I) R can be found in terms of r, a, b, c from this quadratic one for R_(outer) and other R_(inner) . while 2rsin θ=a+c cos 2θ=((2r^2 −(a+c)^2 )/(2r^2 )) ⇒ 2rsin φ=c+b 2rsin ψ=b+a cos (φ+ψ)=sin θ ⇒ (√(1−(((b+c)/(2r)))^2 ))(√(1−(((b+a)/(2r)))^2 )) −(((c+b)(a+b))/(4r^2 ))=((a+c)/(2r)) ⇒ {4r^2 −(b+c)^2 }{4r^2 −(b+a)^2 } =[2r(a+c)+(c+b)(a+b)]^2 ..(II) So we get r from ..(II) and then R from ..(I) ■

$${let}\:{center}\:{of}\:{circumcircle}\:{be}\:{O}. \\ $$$${a}+{c}=\left({R}−{a}\right)\mathrm{sin}\:\alpha_{\mathrm{1}} +\left({R}−{c}\right)\mathrm{sin}\:\beta_{\mathrm{2}} \\ $$$${c}+{b}=\left({R}−{c}\right)\mathrm{sin}\:\beta_{\mathrm{1}} +\left({R}−{b}\right)\mathrm{sin}\:\gamma_{\mathrm{2}} \\ $$$${b}+{a}=\left({R}−{b}\right)\mathrm{sin}\:\gamma_{\mathrm{1}} +\left({R}−{a}\right)\mathrm{sin}\:\alpha_{\mathrm{2}} \\ $$$$\frac{{R}−{a}}{\mathrm{sin}\:\beta_{\mathrm{1}} }=\frac{{R}−{c}}{\mathrm{sin}\:\alpha_{\mathrm{2}} }=\frac{{a}+{c}}{\mathrm{sin}\:\left(\alpha_{\mathrm{2}} +\beta_{\mathrm{1}} \right)}=\mathrm{2}{r} \\ $$$${and}\:{so}\:{on}… \\ $$$${r}\:{being}\:{radius}\:{of}\:{circle}\:{through} \\ $$$${centers}\:{of}\:{circles}\:{A},\:{B},{C}. \\ $$$${adding}\: \\ $$$$\mathrm{2}\left({a}+{b}+{c}\right)=\Sigma\left({R}−{a}\right)\left(\mathrm{sin}\:\alpha_{\mathrm{1}} +\mathrm{sin}\:\alpha_{\mathrm{2}} \right) \\ $$$$\:\:=\Sigma\left({R}−{a}\right)\left(\frac{{R}−{b}}{\mathrm{2}{r}}+\frac{{R}−{c}}{\mathrm{2}{r}}\right) \\ $$$$\Rightarrow\:\mathrm{2}\left({a}+{b}+{c}\right)=\Sigma\left[\frac{\left({R}−{a}\right)\left(\mathrm{2}{R}−{b}−{c}\right)}{\mathrm{2}{r}}\right] \\ $$$$\Rightarrow\:\:\mathrm{4}{r}\left({a}+{b}+{c}\right) \\ $$$$\:\:\:=\mathrm{6}{R}^{\mathrm{2}} −\mathrm{4}{R}\left({a}+{b}+{c}\right)+\mathrm{2}\left({ab}+{bc}+{ca}\right) \\ $$$${but}\:\:\:{if}\:\:{a}+{b}+{c}=\mathrm{2}{s} \\ $$$$\Rightarrow\mathrm{8}{rs}=\mathrm{6}{R}^{\mathrm{2}} −\mathrm{8}{Rs}+\mathrm{4}{s}^{\mathrm{2}} −\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…..\left({I}\right) \\ $$$${R}\:\:{can}\:{be}\:{found}\:{in}\:{terms}\:{of}\: \\ $$$$\:\:\:{r},\:{a},\:{b},\:{c}\:\:\:\:{from}\:{this}\:{quadratic} \\ $$$${one}\:{for}\:{R}_{{outer}} \:\:\:{and}\:{other}\:\:{R}_{{inner}} . \\ $$$${while}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{r}\mathrm{sin}\:\theta={a}+{c} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cos}\:\mathrm{2}\theta=\frac{\mathrm{2}{r}^{\mathrm{2}} −\left({a}+{c}\right)^{\mathrm{2}} }{\mathrm{2}{r}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\:\mathrm{2}{r}\mathrm{sin}\:\phi={c}+{b} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{2}{r}\mathrm{sin}\:\psi={b}+{a} \\ $$$$\mathrm{cos}\:\left(\phi+\psi\right)=\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\:\sqrt{\mathrm{1}−\left(\frac{{b}+{c}}{\mathrm{2}{r}}\right)^{\mathrm{2}} }\sqrt{\mathrm{1}−\left(\frac{{b}+{a}}{\mathrm{2}{r}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:−\frac{\left({c}+{b}\right)\left({a}+{b}\right)}{\mathrm{4}{r}^{\mathrm{2}} }=\frac{{a}+{c}}{\mathrm{2}{r}} \\ $$$$\Rightarrow\:\:\left\{\mathrm{4}{r}^{\mathrm{2}} −\left({b}+{c}\right)^{\mathrm{2}} \right\}\left\{\mathrm{4}{r}^{\mathrm{2}} −\left({b}+{a}\right)^{\mathrm{2}} \right\} \\ $$$$\:\:\:\:\:\:\:=\left[\mathrm{2}{r}\left({a}+{c}\right)+\left({c}+{b}\right)\left({a}+{b}\right)\right]^{\mathrm{2}} \:\:..\left({II}\right) \\ $$$${So}\:{we}\:{get}\:{r}\:{from}\:..\left({II}\right) \\ $$$${and}\:{then}\:\:{R}\:\:{from}\:..\left({I}\right)\:\blacksquare \\ $$$$ \\ $$

Answered by mr W last updated on 09/Jan/20

applying Descartes′ theorem ((1/a)+(1/b)+(1/c)+(1/R))^2 =2((1/a^2 )+(1/b^2 )+(1/c^2 )+(1/R^2 )) ((1/a)+(1/b)+(1/c))^2 +2((1/a)+(1/b)+(1/c))((1/R))=2((1/a^2 )+(1/b^2 )+(1/c^2 ))+(1/R^2 ) (1/R^2 )−2((1/a)+(1/b)+(1/c))((1/R))+((1/a^2 )+(1/b^2 )+(1/c^2 ))−2((1/(ab))+(1/(bc))+(1/(ca)))=0 ⇒(1/R)=((1/a)+(1/b)+(1/c))±(√(((1/a)+(1/b)+(1/c))^2 −((1/a^2 )+(1/b^2 )+(1/c^2 ))+2((1/(ab))+(1/(bc))+(1/(ca))))) ⇒(1/R)=(1/a)+(1/b)+(1/c)±2(√((1/(ab))+(1/(bc))+(1/(ca)))) ⇒R=(1/((1/a)+(1/b)+(1/c)±2(√((1/(ab))+(1/(bc))+(1/(ca)))))) we get two values, since there are two circles which touch the three circles, one is outside (R) and one is inside (r). ⇒R=(1/((1/a)+(1/b)+(1/c)−2(√((1/(ab))+(1/(bc))+(1/(ca)))))) ⇒r=(1/((1/a)+(1/b)+(1/c)+2(√((1/(ab))+(1/(bc))+(1/(ca))))))

$${applying}\:{Descartes}'\:{theorem} \\ $$$$\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}+\frac{\mathrm{1}}{{R}}\right)^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }+\frac{\mathrm{1}}{{R}^{\mathrm{2}} }\right) \\ $$$$\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\right)^{\mathrm{2}} +\mathrm{2}\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\right)\left(\frac{\mathrm{1}}{{R}}\right)=\mathrm{2}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }\right)+\frac{\mathrm{1}}{{R}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{{R}^{\mathrm{2}} }−\mathrm{2}\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\right)\left(\frac{\mathrm{1}}{{R}}\right)+\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }\right)−\mathrm{2}\left(\frac{\mathrm{1}}{{ab}}+\frac{\mathrm{1}}{{bc}}+\frac{\mathrm{1}}{{ca}}\right)=\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{R}}=\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\right)\pm\sqrt{\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }\right)+\mathrm{2}\left(\frac{\mathrm{1}}{{ab}}+\frac{\mathrm{1}}{{bc}}+\frac{\mathrm{1}}{{ca}}\right)} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{R}}=\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\pm\mathrm{2}\sqrt{\frac{\mathrm{1}}{{ab}}+\frac{\mathrm{1}}{{bc}}+\frac{\mathrm{1}}{{ca}}} \\ $$$$\Rightarrow{R}=\frac{\mathrm{1}}{\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\pm\mathrm{2}\sqrt{\frac{\mathrm{1}}{{ab}}+\frac{\mathrm{1}}{{bc}}+\frac{\mathrm{1}}{{ca}}}} \\ $$$${we}\:{get}\:{two}\:{values},\:{since}\:{there}\:{are}\:{two} \\ $$$${circles}\:{which}\:{touch}\:{the}\:{three}\:{circles}, \\ $$$${one}\:{is}\:{outside}\:\left({R}\right)\:{and}\:{one}\:{is}\:{inside}\:\left({r}\right). \\ $$$$\Rightarrow{R}=\frac{\mathrm{1}}{\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}−\mathrm{2}\sqrt{\frac{\mathrm{1}}{{ab}}+\frac{\mathrm{1}}{{bc}}+\frac{\mathrm{1}}{{ca}}}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{1}}{\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}+\mathrm{2}\sqrt{\frac{\mathrm{1}}{{ab}}+\frac{\mathrm{1}}{{bc}}+\frac{\mathrm{1}}{{ca}}}} \\ $$

Commented by mr W last updated on 09/Jan/20

applying Descartes′ theorem ((1/a)+(1/b)+(1/c)+(1/R))^2 =2((1/a^2 )+(1/b^2 )+(1/c^2 )+(1/R^2 )) ((1/d)+(1/b)+(1/c)+(1/R))^2 =2((1/d^2 )+(1/b^2 )+(1/c^2 )+(1/R^2 )) ((1/d)+(1/b)+(1/c)+(1/R))^2 −((1/a)+(1/b)+(1/c)+(1/R))^2 =2((1/d^2 )−(1/a^2 )) ((1/d)−(1/a))((1/d)+(1/a)+(2/b)+(2/c)+(2/R))=2((1/d)−(1/a))((1/d)+(1/a)) −(1/a)+(2/b)+(2/c)+(2/R)=(1/d) (1/a)+(4/b)+(4/c)−4(√((1/(ab))+(1/(bc))+(1/(ca))))=(1/d) ⇒d=(1/((1/a)+(4/b)+(4/c)−4(√((1/(ab))+(1/(bc))+(1/(ca))))))

Commented by jagoll last updated on 09/Jan/20

$${waw}…\:{amazing}\:{sir} \\ $$

Commented by TawaTawa last updated on 09/Jan/20

$$\mathrm{Great},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by mr W last updated on 09/Jan/20

discussion about the result: R=(1/((1/a)+(1/b)+(1/c)−2(√((1/(ab))+(1/(bc))+(1/(ca)))))) r=(1/((1/a)+(1/b)+(1/c)+2(√((1/(ab))+(1/(bc))+(1/(ca)))))) we see that the small circle (r) which touches the three circles from inside always exists, since r>0. concerning the big circle which should touch the three circles from outside, there are following cases: case 1: (1/a)+(1/b)+(1/c)>2(√((1/(ab))+(1/(bc))+(1/(ca)))) R >0, that means the big circle exists, which touches the three circles from outside. it is really a circumcircle. case 2: (1/a)+(1/b)+(1/c)=2(√((1/(ab))+(1/(bc))+(1/(ca)))) R=∞, that means the big circle is in reality a straight line which is a tangent to the three circles. (1/a)+(1/b)+(1/c)=2(√((1/(ab))+(1/(bc))+(1/(ca)))) ((1/a))^2 +2((1/b)+(1/c))(1/a)+((1/b)+(1/c))^2 =4((1/b)+(1/c))(1/a)+4(1/(bc)) ((1/a))^2 −2((1/b)+(1/c))(1/a)+((1/b)−(1/c))^2 =0 ⇒(1/a)=(1/b)+(1/c)±(√(((1/b)+(1/c))^2 −((1/b)−(1/c))^2 )) ⇒(1/a)=(1/b)+(1/c)±2(√(1/(bc)))=((1/( (√b)))±(1/( (√c))))^2 we take the small circle in between, ⇒(1/( (√a)))=(1/( (√b)))+(1/( (√c))) this is a well−known formula. case 3: (1/a)+(1/b)+(1/c)<2(√((1/(ab))+(1/(bc))+(1/(ca)))) R <0, that means the big circle exists, but it touches the three circles from the side. it is an excircle.

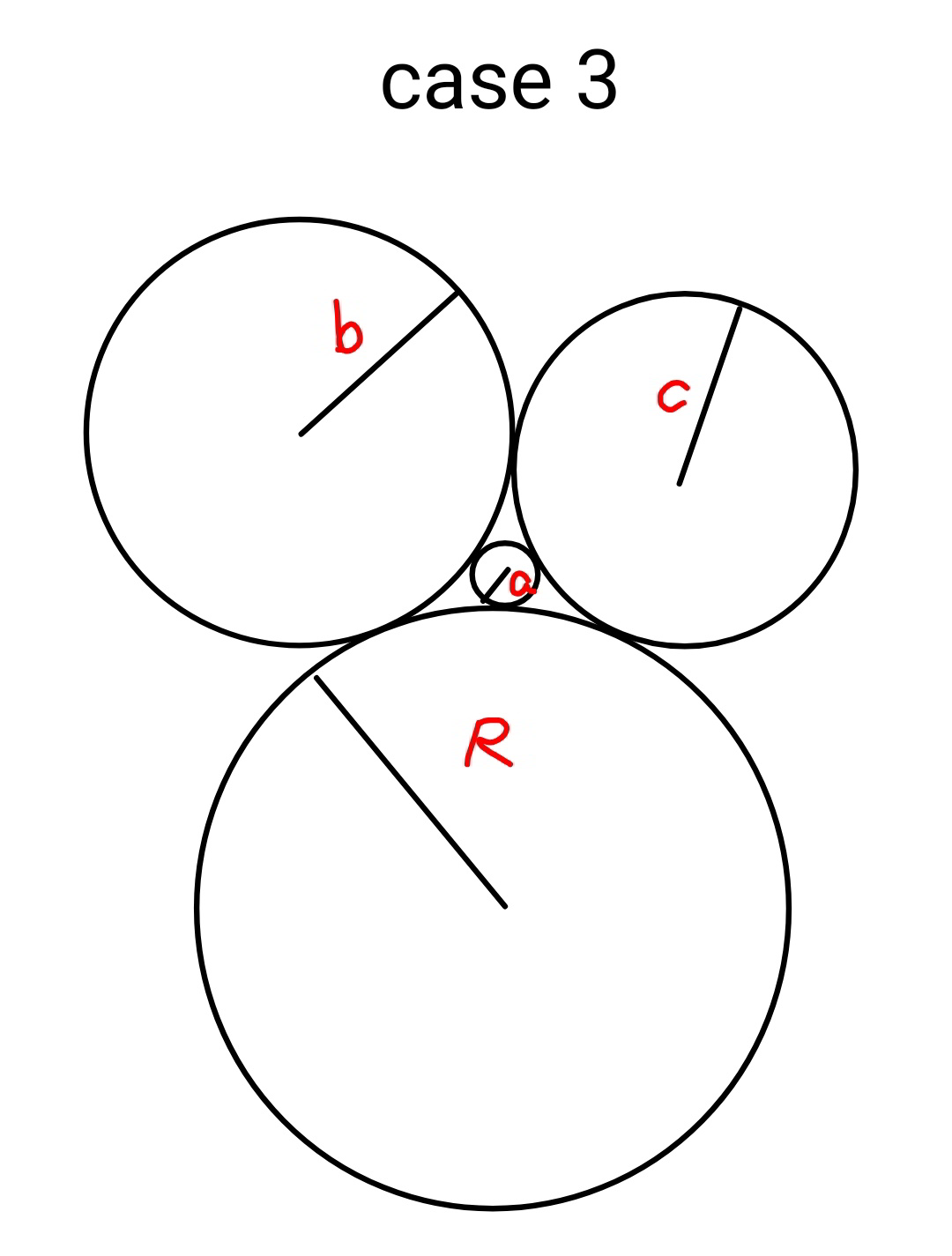
$${discussion}\:{about}\:{the}\:{result}: \\ $$$${R}=\frac{\mathrm{1}}{\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}−\mathrm{2}\sqrt{\frac{\mathrm{1}}{{ab}}+\frac{\mathrm{1}}{{bc}}+\frac{\mathrm{1}}{{ca}}}} \\ $$$${r}=\frac{\mathrm{1}}{\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}+\mathrm{2}\sqrt{\frac{\mathrm{1}}{{ab}}+\frac{\mathrm{1}}{{bc}}+\frac{\mathrm{1}}{{ca}}}} \\ $$$${we}\:{see}\:{that}\:{the}\:{small}\:{circle}\:\left({r}\right)\:{which} \\ $$$${touches}\:{the}\:{three}\:{circles}\:{from}\:{inside} \\ $$$${always}\:{exists},\:{since}\:{r}>\mathrm{0}. \\ $$$$ \\ $$$${concerning}\:{the}\:{big}\:{circle}\:{which}\:{should} \\ $$$${touch}\:{the}\:{three}\:{circles}\:{from}\:{outside}, \\ $$$${there}\:{are}\:{following}\:{cases}: \\ $$$$ \\ $$$${case}\:\mathrm{1}:\:\:\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}>\mathrm{2}\sqrt{\frac{\mathrm{1}}{{ab}}+\frac{\mathrm{1}}{{bc}}+\frac{\mathrm{1}}{{ca}}} \\ $$$${R}\:>\mathrm{0},\:{that}\:{means}\:{the}\:{big}\:{circle}\:{exists}, \\ $$$${which}\:{touches}\:{the}\:{three}\:{circles}\:{from} \\ $$$${outside}.\:{it}\:{is}\:{really}\:{a}\:{circumcircle}. \\ $$$$ \\ $$$${case}\:\mathrm{2}:\:\:\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}=\mathrm{2}\sqrt{\frac{\mathrm{1}}{{ab}}+\frac{\mathrm{1}}{{bc}}+\frac{\mathrm{1}}{{ca}}} \\ $$$${R}=\infty,\:{that}\:{means}\:{the}\:{big}\:{circle}\:{is} \\ $$$${in}\:{reality}\:{a}\:{straight}\:{line}\:{which}\:{is}\:{a} \\ $$$${tangent}\:{to}\:{the}\:{three}\:{circles}.\: \\ $$$$\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}=\mathrm{2}\sqrt{\frac{\mathrm{1}}{{ab}}+\frac{\mathrm{1}}{{bc}}+\frac{\mathrm{1}}{{ca}}} \\ $$$$\left(\frac{\mathrm{1}}{{a}}\right)^{\mathrm{2}} +\mathrm{2}\left(\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\right)\frac{\mathrm{1}}{{a}}+\left(\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\right)^{\mathrm{2}} =\mathrm{4}\left(\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\right)\frac{\mathrm{1}}{{a}}+\mathrm{4}\frac{\mathrm{1}}{{bc}} \\ $$$$\left(\frac{\mathrm{1}}{{a}}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\right)\frac{\mathrm{1}}{{a}}+\left(\frac{\mathrm{1}}{{b}}−\frac{\mathrm{1}}{{c}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{a}}=\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\pm\sqrt{\left(\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{{b}}−\frac{\mathrm{1}}{{c}}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\mathrm{1}}{{a}}=\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\pm\mathrm{2}\sqrt{\frac{\mathrm{1}}{{bc}}}=\left(\frac{\mathrm{1}}{\:\sqrt{{b}}}\pm\frac{\mathrm{1}}{\:\sqrt{{c}}}\right)^{\mathrm{2}} \\ $$$${we}\:{take}\:{the}\:{small}\:{circle}\:{in}\:{between}, \\ $$$$\Rightarrow\frac{\mathrm{1}}{\:\sqrt{{a}}}=\frac{\mathrm{1}}{\:\sqrt{{b}}}+\frac{\mathrm{1}}{\:\sqrt{{c}}} \\ $$$${this}\:{is}\:{a}\:{well}−{known}\:{formula}. \\ $$$$ \\ $$$${case}\:\mathrm{3}:\:\:\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}<\mathrm{2}\sqrt{\frac{\mathrm{1}}{{ab}}+\frac{\mathrm{1}}{{bc}}+\frac{\mathrm{1}}{{ca}}} \\ $$$${R}\:<\mathrm{0},\:{that}\:{means}\:{the}\:{big}\:{circle}\:{exists}, \\ $$$${but}\:{it}\:{touches}\:{the}\:{three}\:{circles}\:{from} \\ $$$${the}\:{side}.\:{it}\:{is}\:{an}\:{excircle}. \\ $$

Commented by mr W last updated on 09/Jan/20

Commented by mr W last updated on 09/Jan/20

Commented by TawaTawa last updated on 09/Jan/20

$$\mathrm{Great}\:\mathrm{sir}.\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}. \\ $$

Commented by Tawa11 last updated on 29/Dec/21

Thanks sir. God bless you more. I see my old account here. Haha ..

$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{more}.\:\mathrm{I}\:\mathrm{see}\:\mathrm{my}\:\mathrm{old}\:\mathrm{account}\:\mathrm{here}.\:\mathrm{Haha}\:.. \\ $$

Commented by Ar Brandon last updated on 29/Dec/21

$$\mathrm{Haha} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply