Question Number 77819 by aliesam last updated on 10/Jan/20
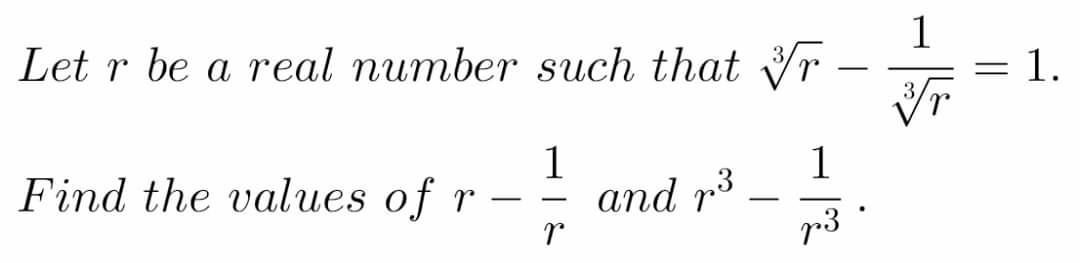
Answered by lémùst last updated on 10/Jan/20

$${posons}\:{t}=\:^{\mathrm{3}} \sqrt{{r}}\:,\:{ainsi}\:{t}\:−\:\frac{\mathrm{1}}{{t}}\:=\:\mathrm{1} \\ $$$$\Rightarrow{t}^{\mathrm{2}} −{t}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{t}=\pm\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${donc}\:{r}=\pm\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{3}} \\ $$$${il}\:{vous}\:{reste}\:{juste}\:{a}\:{calculer}\:{r}−\frac{\mathrm{1}}{{r}}\:{et}\:{r}^{\mathrm{3}} −\frac{\mathrm{1}}{{r}^{\mathrm{3}} } \\ $$$${en}\:{utilisans}\:{les}\:{regles}\:{de}\:{calculs}\:{usuelles} \\ $$
Answered by key of knowledge last updated on 11/Jan/20
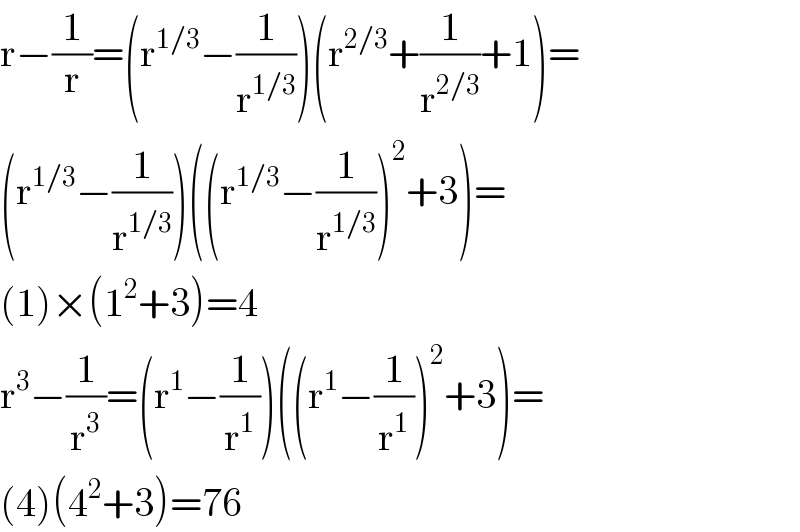
$$\mathrm{r}−\frac{\mathrm{1}}{\mathrm{r}}=\left(\mathrm{r}^{\mathrm{1}/\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{r}^{\mathrm{1}/\mathrm{3}} }\right)\left(\mathrm{r}^{\mathrm{2}/\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{r}^{\mathrm{2}/\mathrm{3}} }+\mathrm{1}\right)= \\ $$$$\left(\mathrm{r}^{\mathrm{1}/\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{r}^{\mathrm{1}/\mathrm{3}} }\right)\left(\left(\mathrm{r}^{\mathrm{1}/\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{r}^{\mathrm{1}/\mathrm{3}} }\right)^{\mathrm{2}} +\mathrm{3}\right)= \\ $$$$\left(\mathrm{1}\right)×\left(\mathrm{1}^{\mathrm{2}} +\mathrm{3}\right)=\mathrm{4} \\ $$$$\mathrm{r}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{r}^{\mathrm{3}} }=\left(\mathrm{r}^{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{r}^{\mathrm{1}} }\right)\left(\left(\mathrm{r}^{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{r}^{\mathrm{1}} }\right)^{\mathrm{2}} +\mathrm{3}\right)= \\ $$$$\left(\mathrm{4}\right)\left(\mathrm{4}^{\mathrm{2}} +\mathrm{3}\right)=\mathrm{76} \\ $$
Commented by aliesam last updated on 10/Jan/20
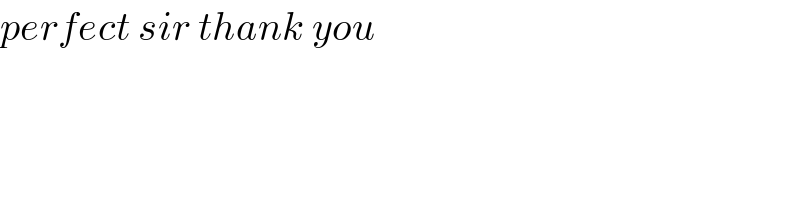
$${perfect}\:{sir}\:{thank}\:{you} \\ $$
Commented by aliesam last updated on 10/Jan/20
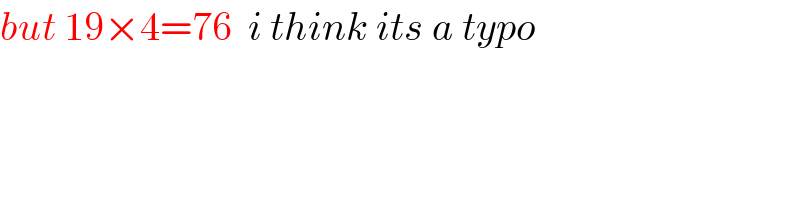
$${but}\:\mathrm{19}×\mathrm{4}=\mathrm{76}\:\:{i}\:{think}\:{its}\:{a}\:{typo} \\ $$
Commented by key of knowledge last updated on 11/Jan/20

$$\mathrm{yes},\mathrm{thank} \\ $$
