Question Number 77883 by TawaTawa last updated on 11/Jan/20
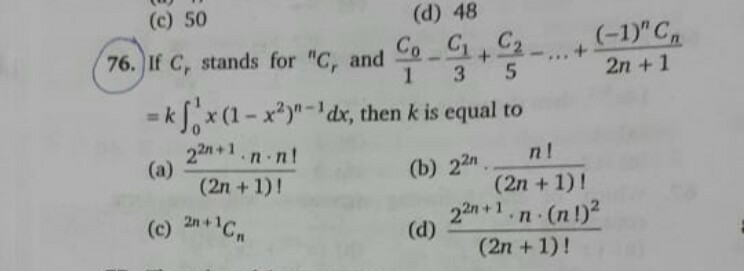
Commented by TawaTawa last updated on 12/Jan/20

$$ \\ $$
Commented by mathmax by abdo last updated on 11/Jan/20
![Σ_(k=0) ^n (((−1)^k )/(2k+1))C_n ^k =k ∫_0 ^1 x(1−x^2 )^(n−1) dx ⇒k=((Σ_(k=0) ^n (((−1)^k )/(2k+1)) C_n ^k )/(∫_0 ^1 x(1−x^2 )^(n−1) dx)) =(A_n /B_n ) let p(x)=Σ_(k=0) ^n (((−1)^k )/(2k+1)) C_n ^k x^(2k+1) ⇒A_n =p(1) p^′ (x)=Σ_(k=0) ^(n ) (−1)^k C_n ^(k ) (x^2 )^k =Σ_(k=0) ^n C_n ^k (−x^2 )^k =(1−x^2 )^n ⇒ p(x)=∫_0 ^x (1−t^2 )^n dt +c we have c=p(0)=0 ⇒p(x)=∫_0 ^x (1−t^2 )^n dt p(1) =∫_0 ^1 (1−t^2 )^n dt =_(t=sinα) ∫_0 ^(π/2) (cos^2 α)^n cosα dα =∫_0 ^(π/2) cos^(2n+1) α dα =A_n ∫_0 ^1 x(1−x^2 )^(n−1) dx =_(x=sinα) ∫_0 ^(π/2) sinα(cos^2 α)^(n−1) cosα dα =∫_0 ^(π/2) sinα cos^(2n−1) α dα =B_n ⇒ k =((∫_0 ^(π/2) cos^(2n+1) αdα)/(∫_0 ^(π/2) sinα cos^(2n−1) α dα)) let A_n =∫_0 ^(π/2) cos_α ^(2n−1) cos^2 α dα =∫_0 ^(π/2) cos^(2n−1) α(1−sin^2 α)dα =∫_0 ^(π/2) cos^(2n−1) α dα +∫_0 ^(π/2) (−sinα cos^(2n−1) α)sinα dα =A_(n−1) +∫_0 ^(π/2) (...)dα by parts u^′ =−sinα cos^(2n−1) α and v=sinα we get ∫_0 ^(π/2) (−sinα cos^(2n−1) α)sinα dα =[(1/(2n))cos^(2n) α sinα]_0 ^(π/2) −(1/(2n))∫_0 ^(π/2) cos^(2n) α cosα dα =−(1/(2n))∫_0 ^(π/2) cos^(2n+1) α dα =−(1/(2n)) A_n ⇒A_n =A_(n−1) −(1/(2n)) A_n ⇒ (1+(1/(2n)))A_n =A_(n−1) ⇒(((2n+1)/(2n))) A_n =A_(n−1) ⇒A_n =((2n)/(2n+1)) A_(n−1) ⇒ Π_(k=1) ^n A_k =Π_(k=1) ^n ((2k)/(2k+1))×Π_(k=1) ^n A_(k−1) ⇒A_1 .A_2 ....A_n =Π_(k=1) ^n ((2k)/(2k+1)).A_0 .A_1 ..A_(n−1) ⇒ A_n =((Π_(k=1) ^n (2k))/(Π_(k=1) ^n (2k+1)))×A_0 =((2^n n!)/(3.5.7.....(2n+1))) (A_0 =1) ⇒ A_n =((2^n n!×2^n n!)/(2.3.4.5....(2n)(2n+1))) =((2^(2n) (n!)^2 )/((2n+1)!)) rest calculus of B_n ...be continued..](https://www.tinkutara.com/question/Q77896.png)
$$\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}+\mathrm{1}}{C}_{{n}} ^{{k}} \:\:={k}\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} \:{dx}\:\Rightarrow{k}=\frac{\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}+\mathrm{1}}\:{C}_{{n}} ^{{k}} }{\int_{\mathrm{0}} ^{\mathrm{1}} {x}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} \:{dx}} \\ $$$$=\frac{{A}_{{n}} }{{B}_{{n}} }\:\:\:{let}\:{p}\left({x}\right)=\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}+\mathrm{1}}\:{C}_{{n}} ^{{k}} \:{x}^{\mathrm{2}{k}+\mathrm{1}} \:\Rightarrow{A}_{{n}} ={p}\left(\mathrm{1}\right) \\ $$$${p}^{'} \left({x}\right)=\sum_{{k}=\mathrm{0}} ^{{n}\:} \:\left(−\mathrm{1}\right)^{{k}} \:{C}_{{n}} ^{{k}\:} \left({x}^{\mathrm{2}} \right)^{{k}} \:\:=\sum_{{k}=\mathrm{0}} ^{{n}} {C}_{{n}} ^{{k}} \left(−{x}^{\mathrm{2}} \right)^{{k}} \:=\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}} \:\Rightarrow \\ $$$${p}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{{n}} \:{dt}\:+{c}\:{we}\:{have}\:{c}={p}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow{p}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{{n}} \:{dt} \\ $$$${p}\left(\mathrm{1}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{{n}} {dt}\:=_{{t}={sin}\alpha} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({cos}^{\mathrm{2}} \alpha\right)^{{n}} \:{cos}\alpha\:{d}\alpha \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{2}{n}+\mathrm{1}} \alpha\:{d}\alpha\:={A}_{{n}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} \:{dx}\:=_{{x}={sin}\alpha} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}\alpha\left({cos}^{\mathrm{2}} \alpha\right)^{{n}−\mathrm{1}} \:{cos}\alpha\:{d}\alpha \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}\alpha\:{cos}^{\mathrm{2}{n}−\mathrm{1}} \alpha\:{d}\alpha\:={B}_{{n}} \:\Rightarrow\:{k}\:=\frac{\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{2}{n}+\mathrm{1}} \alpha{d}\alpha}{\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}\alpha\:{cos}^{\mathrm{2}{n}−\mathrm{1}} \alpha\:{d}\alpha} \\ $$$${let}\:\:{A}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}_{\alpha} ^{\mathrm{2}{n}−\mathrm{1}} \:{cos}^{\mathrm{2}} \alpha\:{d}\alpha\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{2}{n}−\mathrm{1}} \alpha\left(\mathrm{1}−{sin}^{\mathrm{2}} \alpha\right){d}\alpha \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{2}{n}−\mathrm{1}} \alpha\:{d}\alpha\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left(−{sin}\alpha\:{cos}^{\mathrm{2}{n}−\mathrm{1}} \alpha\right){sin}\alpha\:{d}\alpha \\ $$$$={A}_{{n}−\mathrm{1}} +\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(…\right){d}\alpha\:\:{by}\:{parts}\:\:{u}^{'} =−{sin}\alpha\:{cos}^{\mathrm{2}{n}−\mathrm{1}} \alpha\:{and}\:{v}={sin}\alpha \\ $$$${we}\:{get}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(−{sin}\alpha\:{cos}^{\mathrm{2}{n}−\mathrm{1}} \alpha\right){sin}\alpha\:{d}\alpha \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{2}{n}}{cos}^{\mathrm{2}{n}} \alpha\:{sin}\alpha\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\frac{\mathrm{1}}{\mathrm{2}{n}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:{cos}^{\mathrm{2}{n}} \alpha\:{cos}\alpha\:{d}\alpha \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}{n}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{2}{n}+\mathrm{1}} \alpha\:{d}\alpha\:=−\frac{\mathrm{1}}{\mathrm{2}{n}}\:{A}_{{n}} \:\Rightarrow{A}_{{n}} ={A}_{{n}−\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}{n}}\:{A}_{{n}} \:\Rightarrow \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}}\right){A}_{{n}} \:={A}_{{n}−\mathrm{1}} \:\Rightarrow\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}{n}}\right)\:{A}_{{n}} ={A}_{{n}−\mathrm{1}} \:\Rightarrow{A}_{{n}} =\frac{\mathrm{2}{n}}{\mathrm{2}{n}+\mathrm{1}}\:{A}_{{n}−\mathrm{1}} \:\Rightarrow \\ $$$$\prod_{{k}=\mathrm{1}} ^{{n}} \:{A}_{{k}} =\prod_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{2}{k}}{\mathrm{2}{k}+\mathrm{1}}×\prod_{{k}=\mathrm{1}} ^{{n}} {A}_{{k}−\mathrm{1}} \:\:\Rightarrow{A}_{\mathrm{1}} .{A}_{\mathrm{2}} ….{A}_{{n}} =\prod_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{2}{k}}{\mathrm{2}{k}+\mathrm{1}}.{A}_{\mathrm{0}} .{A}_{\mathrm{1}} ..{A}_{{n}−\mathrm{1}} \\ $$$$\Rightarrow\:{A}_{{n}} =\frac{\prod_{{k}=\mathrm{1}} ^{{n}} \left(\mathrm{2}{k}\right)}{\prod_{{k}=\mathrm{1}} ^{{n}} \left(\mathrm{2}{k}+\mathrm{1}\right)}×{A}_{\mathrm{0}} \:\:=\frac{\mathrm{2}^{{n}} \:{n}!}{\mathrm{3}.\mathrm{5}.\mathrm{7}…..\left(\mathrm{2}{n}+\mathrm{1}\right)}\:\:\left({A}_{\mathrm{0}} =\mathrm{1}\right) \\ $$$$\Rightarrow\:{A}_{{n}} =\frac{\mathrm{2}^{{n}} {n}!×\mathrm{2}^{{n}} {n}!}{\mathrm{2}.\mathrm{3}.\mathrm{4}.\mathrm{5}….\left(\mathrm{2}{n}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}\:=\frac{\mathrm{2}^{\mathrm{2}{n}} \left({n}!\right)^{\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$${rest}\:{calculus}\:{of}\:{B}_{{n}} …{be}\:{continued}.. \\ $$
Commented by TawaTawa last updated on 11/Jan/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{waiting}\:\mathrm{for}\:\mathrm{the}\:\mathrm{rest}. \\ $$
Commented by mathmax by abdo last updated on 12/Jan/20
![B_n =∫_0 ^(π/2) sinα cos^(2n−1) α dα =[−(1/(2n))cos^(2n) α]_0 ^(π/2) =(1/(2n)) ⇒ k=(A_n /B_n ) =((2^(2n) (n!)^2 )/((2n+1)!))×(2n) =((2^(2n+1) n(n!)^2 )/((2n+1)!))](https://www.tinkutara.com/question/Q77903.png)
$${B}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}\alpha\:{cos}^{\mathrm{2}{n}−\mathrm{1}} \alpha\:{d}\alpha\:=\left[−\frac{\mathrm{1}}{\mathrm{2}{n}}{cos}^{\mathrm{2}{n}} \alpha\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\mathrm{1}}{\mathrm{2}{n}}\:\Rightarrow \\ $$$${k}=\frac{{A}_{{n}} }{{B}_{{n}} }\:=\frac{\mathrm{2}^{\mathrm{2}{n}} \left({n}!\right)^{\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}×\left(\mathrm{2}{n}\right)\:=\frac{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} {n}\left({n}!\right)^{\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$
Commented by mathmax by abdo last updated on 12/Jan/20
$${so}\:{the}\:{correct}\:{answer}\:{is}\:\left({d}\right) \\ $$
Commented by TawaTawa last updated on 12/Jan/20
$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Commented by TawaTawa last updated on 12/Jan/20
$$\mathrm{Sir},\:\mathrm{please}\:\mathrm{help}\:\mathrm{with}\:\:\mathrm{16}\:\mathrm{and}\:\mathrm{17}\:\mathrm{in}\:\mathrm{question}\:\mathrm{77881} \\ $$
Answered by mr W last updated on 12/Jan/20
![(1−x^2 )^n =Σ_(r=0) ^n C_r ^n (−x^2 )^r =Σ_(r=0) ^n (−1)^r C_r x^(2r) ∫_0 ^1 (1−x^2 )^n dx=Σ_(r=0) ^n (−1)^r C_r ∫_0 ^1 x^(2r) dx ∫_0 ^1 (1−x^2 )^n dx=Σ_(r=0) ^n (((−1)^r C_r )/(2r+1))=(C_0 /1)−(C_1 /3)+(C_2 /5)−...+(((−1)^n C_n )/(2n+1)) let I_n =∫_0 ^1 (1−x^2 )^n dx I_n =[x(1−x^2 )^n ]_0 ^1 −∫_0 ^1 x×n(1−x^2 )^(n−1) (−2x)dx =0+2n∫_0 ^1 x^2 (1−x^2 )^(n−1) dx =−2n[∫_0 ^1 (1−x^2 )^(n−1) dx−∫_0 ^1 x^2 (1−x^2 )^(n−1) dx−∫_0 ^1 (1−x^2 )^(n−1) dx] =−2n[∫_0 ^1 (1−x^2 )^n dx−∫_0 ^1 (1−x^2 )^(n−1) dx] =−2n[I_n −I_(n−1) ] I_n =−2nI_n +2nI_(n−1) ⇒I_n =((2n)/(2n+1))I_(n−1) ⇒I_n =((2n)/(2n+1))×((2(n−1))/(2n−1))×...×((2×1)/(2×1+1))I_0 I_0 =∫_0 ^1 (1−x^2 )^0 dx=1 ⇒I_n =((2^n n!)/((2n+1)!!))=((2^n n!(2n)!!)/((2n+1)!!(2n)!!))=((2^(2n) (n!)^2 )/((2n+1)!)) let J=∫_0 ^1 x(1−x^2 )^(n−1) dx J=−(1/2)∫_0 ^1 (1−x^2 )^(n−1) d(1−x^2 ) =−[(((1−x^2 )^n )/(2n))]_0 ^1 =(1/(2n)) I_n =kJ ((2^(2n) (n!)^2 )/((2n+1)!))=k×(1/(2n)) ⇒k=((2^(2n+1) ∙n∙(n!)^2 )/((2n+1)!)) (=((2^(n+1) ∙n∙n!)/((2n+1)!!))) ⇒answer D is correct](https://www.tinkutara.com/question/Q77895.png)
$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}} =\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{r}} ^{{n}} \left(−{x}^{\mathrm{2}} \right)^{{r}} =\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{r}} {C}_{{r}} {x}^{\mathrm{2}{r}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}} {dx}=\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{r}} {C}_{{r}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}{r}} {dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}} {dx}=\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{r}} {C}_{{r}} }{\mathrm{2}{r}+\mathrm{1}}=\frac{{C}_{\mathrm{0}} }{\mathrm{1}}−\frac{{C}_{\mathrm{1}} }{\mathrm{3}}+\frac{{C}_{\mathrm{2}} }{\mathrm{5}}−…+\frac{\left(−\mathrm{1}\right)^{{n}} {C}_{{n}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$${let}\:{I}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}} {dx} \\ $$$${I}_{{n}} =\left[{x}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}} \right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} {x}×{n}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} \left(−\mathrm{2}{x}\right){dx} \\ $$$$=\mathrm{0}+\mathrm{2}{n}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} {dx} \\ $$$$=−\mathrm{2}{n}\left[\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} {dx}−\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} {dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} {dx}\right] \\ $$$$=−\mathrm{2}{n}\left[\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}} {dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} {dx}\right] \\ $$$$=−\mathrm{2}{n}\left[{I}_{{n}} −{I}_{{n}−\mathrm{1}} \right] \\ $$$${I}_{{n}} =−\mathrm{2}{nI}_{{n}} +\mathrm{2}{nI}_{{n}−\mathrm{1}} \\ $$$$\Rightarrow{I}_{{n}} =\frac{\mathrm{2}{n}}{\mathrm{2}{n}+\mathrm{1}}{I}_{{n}−\mathrm{1}} \\ $$$$\Rightarrow{I}_{{n}} =\frac{\mathrm{2}{n}}{\mathrm{2}{n}+\mathrm{1}}×\frac{\mathrm{2}\left({n}−\mathrm{1}\right)}{\mathrm{2}{n}−\mathrm{1}}×…×\frac{\mathrm{2}×\mathrm{1}}{\mathrm{2}×\mathrm{1}+\mathrm{1}}{I}_{\mathrm{0}} \\ $$$${I}_{\mathrm{0}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{0}} {dx}=\mathrm{1} \\ $$$$\Rightarrow{I}_{{n}} =\frac{\mathrm{2}^{{n}} {n}!}{\left(\mathrm{2}{n}+\mathrm{1}\right)!!}=\frac{\mathrm{2}^{{n}} {n}!\left(\mathrm{2}{n}\right)!!}{\left(\mathrm{2}{n}+\mathrm{1}\right)!!\left(\mathrm{2}{n}\right)!!}=\frac{\mathrm{2}^{\mathrm{2}{n}} \left({n}!\right)^{\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$${let}\:{J}=\int_{\mathrm{0}} ^{\mathrm{1}} {x}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} {dx} \\ $$$${J}=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} {d}\left(\mathrm{1}−{x}^{\mathrm{2}} \right) \\ $$$$=−\left[\frac{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}} }{\mathrm{2}{n}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{n}} \\ $$$$ \\ $$$${I}_{{n}} ={kJ} \\ $$$$\frac{\mathrm{2}^{\mathrm{2}{n}} \left({n}!\right)^{\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}={k}×\frac{\mathrm{1}}{\mathrm{2}{n}} \\ $$$$\Rightarrow{k}=\frac{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} \centerdot{n}\centerdot\left({n}!\right)^{\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:\:\:\left(=\frac{\mathrm{2}^{{n}+\mathrm{1}} \centerdot{n}\centerdot{n}!}{\left(\mathrm{2}{n}+\mathrm{1}\right)!!}\right) \\ $$$$\Rightarrow{answer}\:{D}\:{is}\:{correct} \\ $$
Commented by TawaTawa last updated on 12/Jan/20

$$\mathrm{You}\:\mathrm{are}\:\mathrm{right}\:\mathrm{sir}.\:\:\mathrm{Option}\:\mathrm{D}\:\mathrm{is}\:\mathrm{correct}. \\ $$$$\mathrm{I}\:\mathrm{just}\:\mathrm{check}\:\mathrm{it}\:\mathrm{well}\:\mathrm{now}. \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by TawaTawa last updated on 12/Jan/20
$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}. \\ $$
Commented by TawaTawa last updated on 12/Jan/20
$$\mathrm{Sir}\:\mathrm{please}\:\mathrm{help}\:\mathrm{withquestion}\:\:\mathrm{77902}. \\ $$
