Question Number 78056 by ajfour last updated on 13/Jan/20
Answered by ajfour last updated on 13/Jan/20
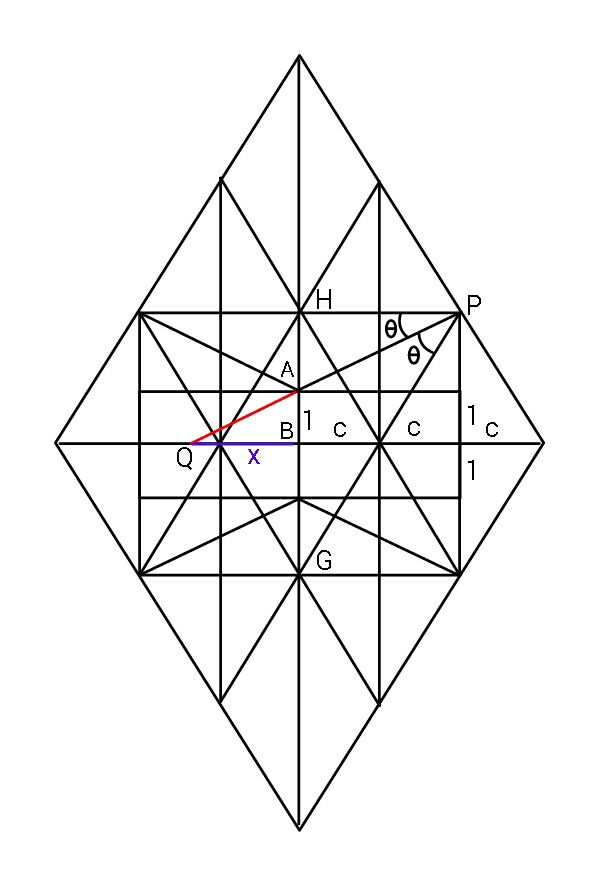
![It is from aid of another diagram that x^3 −x=2c ....(i) From here first let AH=r tan θ=(1/x)=(r/(2c)) .....(ii) Also considering △GHP ((AH)/(AG))=((PH)/(PG)) ⇒ (r/(2+r))=((2c)/( (√((2c)^2 +[2(r+1)]^2 )))) ..(iii) using (ii) in (i) (((2c)^3 )/r^3 )−((2c)/r)= 2c .....(I) Solving for common root of (iii) & (I) should give a new type of solution, and an alter- native to Cardano′s method, for x^3 −x=2c , which gets difficult if c^2 <((1/3))^3 ... I shall carry on..](https://www.tinkutara.com/question/Q78057.png)
$${It}\:{is}\:{from}\:{aid}\:{of}\:{another} \\ $$$${diagram}\:{that}\:{x}^{\mathrm{3}} −{x}=\mathrm{2}{c}\:\:\:\:….\left({i}\right) \\ $$$${From}\:{here} \\ $$$${first}\:{let}\:{AH}={r} \\ $$$$\mathrm{tan}\:\theta=\frac{\mathrm{1}}{{x}}=\frac{{r}}{\mathrm{2}{c}}\:\:\:\:\:\:\:\:\:\:…..\left({ii}\right) \\ $$$${Also}\:{considering}\:\bigtriangleup{GHP} \\ $$$$\:\:\:\frac{{AH}}{{AG}}=\frac{{PH}}{{PG}} \\ $$$$\Rightarrow\:\frac{{r}}{\mathrm{2}+{r}}=\frac{\mathrm{2}{c}}{\:\sqrt{\left(\mathrm{2}{c}\right)^{\mathrm{2}} +\left[\mathrm{2}\left({r}+\mathrm{1}\right)\right]^{\mathrm{2}} }}\:\:\:..\left({iii}\right) \\ $$$$ \\ $$$${using}\:\left({ii}\right)\:{in}\:\left({i}\right) \\ $$$$\:\:\:\frac{\left(\mathrm{2}{c}\right)^{\mathrm{3}} }{{r}^{\mathrm{3}} }−\frac{\mathrm{2}{c}}{{r}}=\:\mathrm{2}{c}\:\:\:\:\:\:\:\:…..\left({I}\right) \\ $$$${Solving}\:{for}\:{common}\:{root}\:{of} \\ $$$$\left({iii}\right)\:\&\:\left({I}\right)\:{should}\:{give}\:{a}\:{new} \\ $$$${type}\:{of}\:{solution},\:{and}\:{an}\:{alter}- \\ $$$${native}\:{to}\:{Cardano}'{s}\:{method}, \\ $$$${for}\:\:{x}^{\mathrm{3}} −{x}=\mathrm{2}{c}\:,\:{which}\:{gets} \\ $$$${difficult}\:{if}\:\:{c}^{\mathrm{2}} <\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{3}} … \\ $$$${I}\:{shall}\:{carry}\:{on}.. \\ $$$$ \\ $$$$ \\ $$
Commented by ajfour last updated on 13/Jan/20
![⇒ (r/(2+r))=((2c)/( (√((2c)^2 +[2(r+1)]^2 )))) ..(iii) let r+1=t r+1=((2c)/x)+1 So (((2c/x))/((((2c)/x)+2)))=(c/( (√(c^2 +(((2c)/x)+1)^2 )))) but x^2 −((2c)/x) = 1 ( As x^3 −x=2c ) ⇒ x^2 −r=1 & As (r/(r+2))=(c/( (√(c^2 +x^4 )))) ⇒ r^2 x^4 = 4c^2 r+4c^2 ⇒ r^2 x^4 = 4c^2 x^2 ⇒ rx=2c So the simplest it can get is { ((x^2 −r=1)),((rx=c)) :} ................... ! ....................](https://www.tinkutara.com/question/Q78058.png)
$$\Rightarrow\:\frac{{r}}{\mathrm{2}+{r}}=\frac{\mathrm{2}{c}}{\:\sqrt{\left(\mathrm{2}{c}\right)^{\mathrm{2}} +\left[\mathrm{2}\left({r}+\mathrm{1}\right)\right]^{\mathrm{2}} }}\:\:\:..\left({iii}\right) \\ $$$$\:\:\:{let}\:\:{r}+\mathrm{1}={t} \\ $$$$\:\:{r}+\mathrm{1}=\frac{\mathrm{2}{c}}{{x}}+\mathrm{1} \\ $$$${So}\:\:\:\:\:\frac{\left(\mathrm{2}{c}/{x}\right)}{\left(\frac{\mathrm{2}{c}}{{x}}+\mathrm{2}\right)}=\frac{{c}}{\:\sqrt{{c}^{\mathrm{2}} +\left(\frac{\mathrm{2}{c}}{{x}}+\mathrm{1}\right)^{\mathrm{2}} }} \\ $$$${but} \\ $$$$\:{x}^{\mathrm{2}} −\frac{\mathrm{2}{c}}{{x}}\:=\:\mathrm{1}\:\:\:\:\:\:\:\:\:\left(\:\:{As}\:{x}^{\mathrm{3}} −{x}=\mathrm{2}{c}\:\:\right) \\ $$$$\Rightarrow\:\:{x}^{\mathrm{2}} −{r}=\mathrm{1}\:\:\:\:\:\&\:\: \\ $$$${As}\:\:\:\:\frac{{r}}{{r}+\mathrm{2}}=\frac{{c}}{\:\sqrt{{c}^{\mathrm{2}} +{x}^{\mathrm{4}} }} \\ $$$$\Rightarrow\:\:\:\:{r}^{\mathrm{2}} {x}^{\mathrm{4}} \:=\:\mathrm{4}{c}^{\mathrm{2}} {r}+\mathrm{4}{c}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{r}^{\mathrm{2}} {x}^{\mathrm{4}} =\:\mathrm{4}{c}^{\mathrm{2}} {x}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:{rx}=\mathrm{2}{c} \\ $$$${So}\:{the}\:{simplest}\:{it}\:{can}\:{get}\:{is} \\ $$$$\:\:\:\:\begin{cases}{{x}^{\mathrm{2}} −{r}=\mathrm{1}}\\{{rx}={c}}\end{cases}\:\:\:\: \\ $$$$……………….\:\:\:!\:\:……………….. \\ $$
