Question Number 78105 by aliesam last updated on 14/Jan/20
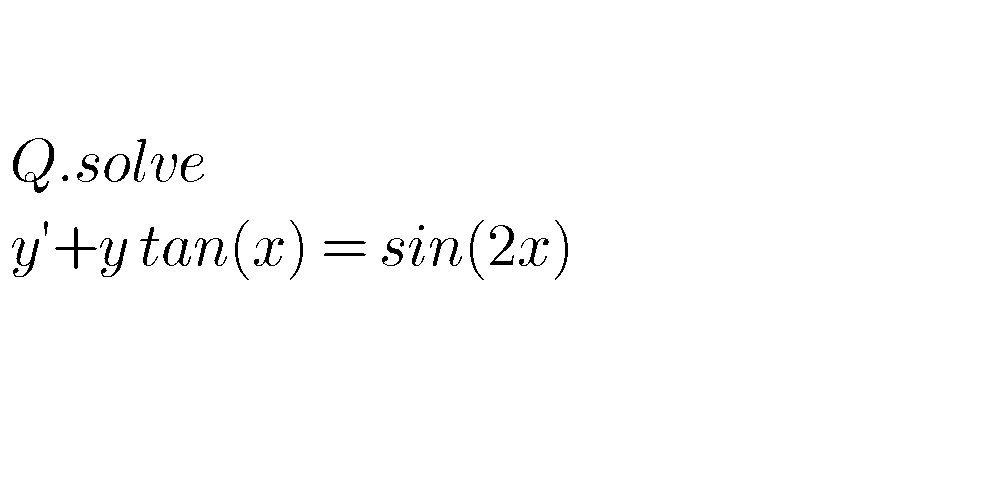
Answered by Kunal12588 last updated on 14/Jan/20

$$\frac{{dy}}{{dx}}+\left({tan}\:{x}\right){y}={sin}\:\mathrm{2}{x} \\ $$$${This}\:{is}\:{a}\:{linear}\:{differential}\:{equation} \\ $$$${differential}\:{equation}\:{of}\:{the}\:{type} \\ $$$$\frac{{dy}}{{dx}}+{Px}={Q}\:\:;\:{P}\:\&\:{Q}\:{are}\:{function}\:{of}\:{x}\:{only} \\ $$$${P}\:=\:{tan}\:{x},\:{Q}\:=\:{sin}\:\mathrm{2}{x} \\ $$$${I}.{F}.\:=\:{e}^{\int{P}\:{dx}} \\ $$$$\Rightarrow{I}.{F}.\:=\:{e}^{\int{tan}\:{x}\:{dx}} \\ $$$$\Rightarrow{I}.{F}.\:=\:{e}^{{log}\:\mid{sec}\:{x}\mid} ={sec}\:{x} \\ $$$${solution}\:{of}\:{differential}\:{equation} \\ $$$${y}\left({I}.{F}\right)=\int\left({I}.{F}\right)×{Q}\:{dx} \\ $$$$\Rightarrow{y}\:{sec}\:{x}\:=\:\int\:{sec}\:{x}\:\mathrm{2}\:{sin}\:{x}\:{cos}\:{x}\:{sx} \\ $$$$\Rightarrow{y}\:{sec}\:{x}\:=\:\mathrm{2}\:\int\:{sin}\:{x}\:{dx} \\ $$$$\Rightarrow{y}\:{sec}\:{x}\:=\:−\:\mathrm{2}\:{cos}\:{x}\:+\:{C} \\ $$$$\Rightarrow{y}=\:−\mathrm{2}\:{cos}^{\mathrm{2}} {x}\:+\:{C}\:{cos}\:{x} \\ $$
