Question Number 78216 by TawaTawa last updated on 15/Jan/20
Commented by TawaTawa last updated on 15/Jan/20
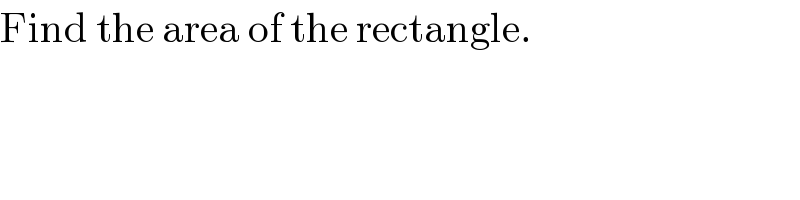
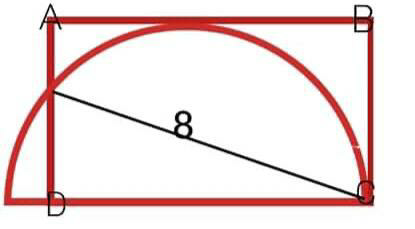
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{rectangle}. \\ $$
Commented by mr W last updated on 15/Jan/20
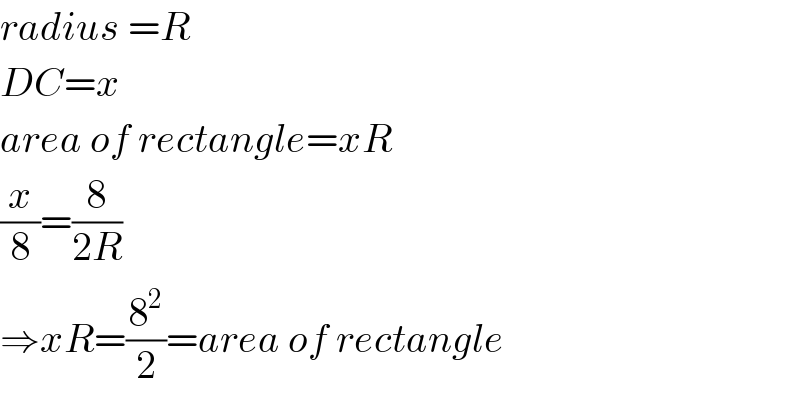
$${radius}\:={R} \\ $$$${DC}={x} \\ $$$${area}\:{of}\:{rectangle}={xR} \\ $$$$\frac{{x}}{\mathrm{8}}=\frac{\mathrm{8}}{\mathrm{2}{R}} \\ $$$$\Rightarrow{xR}=\frac{\mathrm{8}^{\mathrm{2}} }{\mathrm{2}}={area}\:{of}\:{rectangle} \\ $$
Commented by Tony Lin last updated on 15/Jan/20
Commented by Tony Lin last updated on 15/Jan/20
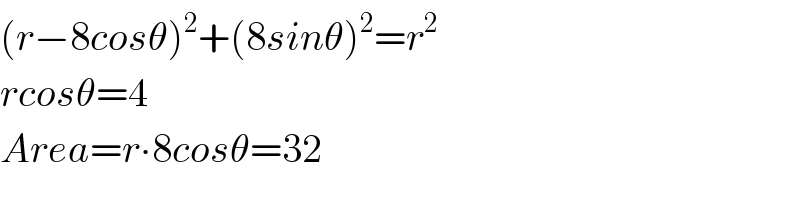
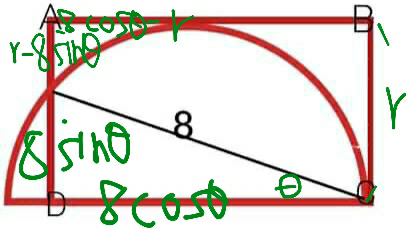
$$\left({r}−\mathrm{8}{cos}\theta\right)^{\mathrm{2}} +\left(\mathrm{8}{sin}\theta\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${rcos}\theta=\mathrm{4} \\ $$$${Area}={r}\centerdot\mathrm{8}{cos}\theta=\mathrm{32} \\ $$
Commented by TawaTawa last updated on 15/Jan/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 15/Jan/20

$$\frac{\mathrm{8}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{32} \\ $$
Commented by jagoll last updated on 15/Jan/20

$${very}\:{simple}\:{sir} \\ $$
Commented by TawaTawa last updated on 15/Jan/20

$$\mathrm{Why}\:\mathrm{sir}. \\ $$
Commented by TawaTawa last updated on 15/Jan/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
