Question-7824

Question Number 7824 by ridwan balatif last updated on 17/Sep/16

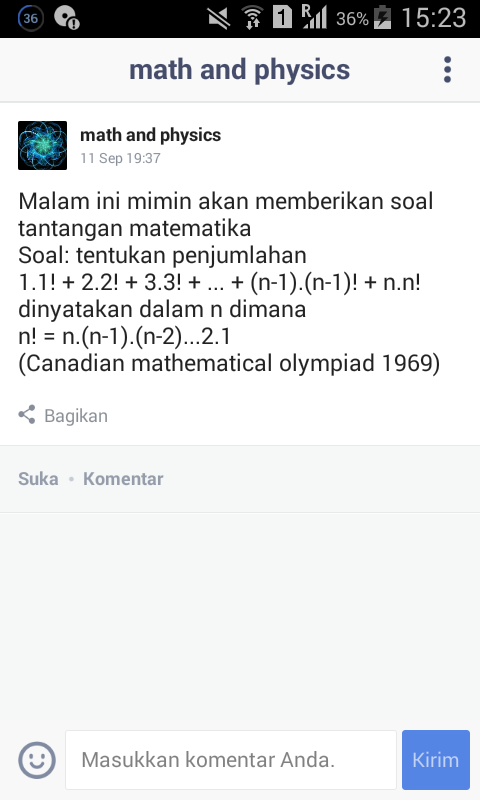
Commented by Yozzia last updated on 17/Sep/16

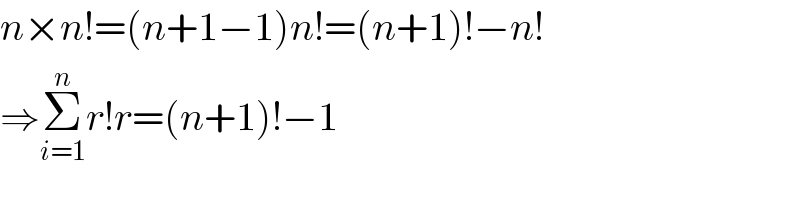
n×n!=(n+1−1)n!=(n+1)!−n! ⇒Σ_(i=1) ^n r!r=(n+1)!−1

$${n}×{n}!=\left({n}+\mathrm{1}−\mathrm{1}\right){n}!=\left({n}+\mathrm{1}\right)!−{n}! \\ $$$$\Rightarrow\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{r}!{r}=\left({n}+\mathrm{1}\right)!−\mathrm{1} \\ $$

Commented by prakash jain last updated on 17/Sep/16

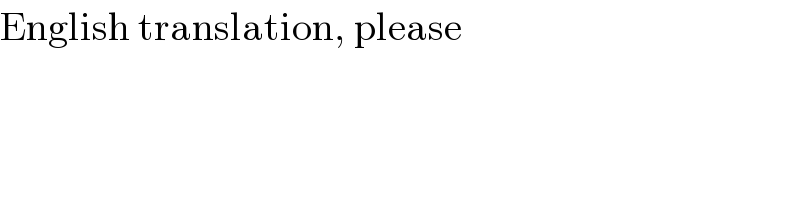
$$\mathrm{English}\:\mathrm{translation},\:\mathrm{please} \\ $$

Commented by ridwan balatif last updated on 17/Sep/16

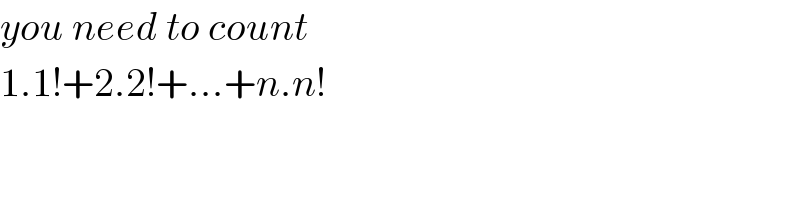
$${you}\:{need}\:{to}\:{count} \\ $$$$\mathrm{1}.\mathrm{1}!+\mathrm{2}.\mathrm{2}!+…+{n}.{n}! \\ $$

Commented by FilupSmith last updated on 17/Sep/16

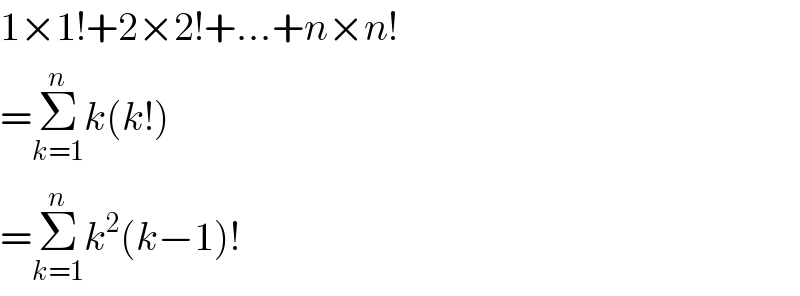
1×1!+2×2!+...+n×n! =Σ_(k=1) ^n k(k!) =Σ_(k=1) ^n k^2 (k−1)!

$$\mathrm{1}×\mathrm{1}!+\mathrm{2}×\mathrm{2}!+…+{n}×{n}! \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}\left({k}!\right) \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} \left({k}−\mathrm{1}\right)! \\ $$

Answered by prakash jain last updated on 02/Oct/16

$$\mathrm{see}\:\mathrm{comments} \\ $$

Facebook Tweet Pin

Question-7824

Leave a Reply Cancel reply