Menu Close

Question-78289

Tinku Tara 0 Comments
Pin




Question Number 78289 by ajfour last updated on 15/Jan/20
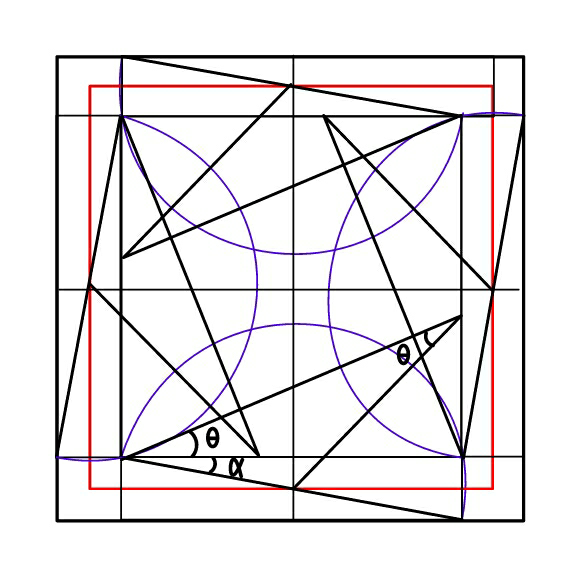
Commented by ajfour last updated on 15/Jan/20
Find θ , given α.
$${Find}\:\theta\:,\:{given}\:\alpha. \\ $$
Answered by mr W last updated on 15/Jan/20
R=radius ((2R cos α)/(cos θ sin (2θ+α)))=(R/(sin θ)) ((sin (2θ+α))/(cos α))=((2 sin θ)/(cos θ)) ((sin (2θ) cos α+cos (2θ) sin α)/(cos α))=2 tan θ sin (2θ)+tan α cos (2θ)=2 tan θ tan α(2 cos^2 θ−1)=2 tan θ (1−cos^2 θ) tan α((2/(1+tan^2 θ))−1)=2 tan θ (1−(1/(1+tan^2 θ))) tan α(((1−tan^2 θ)/(1+tan^2 θ)))=2 tan θ (((tan^2 θ)/(1+tan^2 θ))) tan α(1−tan^2 θ)=2 tan^3 θ ⇒(1/(tan^3 θ))−(1/(tan θ))−(2/(tan α))=0 let t=(1/(tan θ)), a=(1/(tan α)) ⇒t^3 −t−2a=0 ⇒t=(((√(a^2 −(1/(27))))+a))^(1/3) −(((√(a^2 −(1/(27))))−a))^(1/3) ⇒(1/(tan θ))=(((√((1/(tan^2 α))−(1/(27))))+(1/(tan α))))^(1/3) −(((√((1/(tan^2 α))−(1/(27))))−(1/(tan α))))^(1/3) ⇒θ=(π/2)−tan^(−1) ((((√((1/(tan^2 α))−(1/(27))))+(1/(tan α))))^(1/3) −(((√((1/(tan^2 α))−(1/(27))))−(1/(tan α))))^(1/3) )
$${R}={radius} \\ $$$$\frac{\mathrm{2}{R}\:\mathrm{cos}\:\alpha}{\mathrm{cos}\:\theta\:\mathrm{sin}\:\left(\mathrm{2}\theta+\alpha\right)}=\frac{{R}}{\mathrm{sin}\:\theta} \\ $$$$\frac{\mathrm{sin}\:\left(\mathrm{2}\theta+\alpha\right)}{\mathrm{cos}\:\alpha}=\frac{\mathrm{2}\:\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta} \\ $$$$\frac{\mathrm{sin}\:\left(\mathrm{2}\theta\right)\:\mathrm{cos}\:\alpha+\mathrm{cos}\:\left(\mathrm{2}\theta\right)\:\mathrm{sin}\:\alpha}{\mathrm{cos}\:\alpha}=\mathrm{2}\:\mathrm{tan}\:\theta \\ $$$$\mathrm{sin}\:\left(\mathrm{2}\theta\right)+\mathrm{tan}\:\alpha\:\mathrm{cos}\:\left(\mathrm{2}\theta\right)=\mathrm{2}\:\mathrm{tan}\:\theta \\ $$$$\mathrm{tan}\:\alpha\left(\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{1}\right)=\mathrm{2}\:\mathrm{tan}\:\theta\:\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\theta\right) \\ $$$$\mathrm{tan}\:\alpha\left(\frac{\mathrm{2}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta}−\mathrm{1}\right)=\mathrm{2}\:\mathrm{tan}\:\theta\:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta}\right) \\ $$$$\mathrm{tan}\:\alpha\left(\frac{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\theta}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta}\right)=\mathrm{2}\:\mathrm{tan}\:\theta\:\left(\frac{\mathrm{tan}^{\mathrm{2}} \:\theta}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta}\right) \\ $$$$\mathrm{tan}\:\alpha\left(\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\theta\right)=\mathrm{2}\:\mathrm{tan}^{\mathrm{3}} \:\theta \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{3}} \:\theta}−\frac{\mathrm{1}}{\mathrm{tan}\:\theta}−\frac{\mathrm{2}}{\mathrm{tan}\:\alpha}=\mathrm{0} \\ $$$${let}\:{t}=\frac{\mathrm{1}}{\mathrm{tan}\:\theta},\:{a}=\frac{\mathrm{1}}{\mathrm{tan}\:\alpha} \\ $$$$\Rightarrow{t}^{\mathrm{3}} −{t}−\mathrm{2}{a}=\mathrm{0} \\ $$$$\Rightarrow{t}=\sqrt[{\mathrm{3}}]{\sqrt{{a}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{27}}}+{a}}−\sqrt[{\mathrm{3}}]{\sqrt{{a}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{27}}}−{a}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{tan}\:\theta}=\sqrt[{\mathrm{3}}]{\sqrt{\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \:\alpha}−\frac{\mathrm{1}}{\mathrm{27}}}+\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}}−\sqrt[{\mathrm{3}}]{\sqrt{\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \:\alpha}−\frac{\mathrm{1}}{\mathrm{27}}}−\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}} \\ $$$$\Rightarrow\theta=\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} \left(\sqrt[{\mathrm{3}}]{\sqrt{\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \:\alpha}−\frac{\mathrm{1}}{\mathrm{27}}}+\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}}−\sqrt[{\mathrm{3}}]{\sqrt{\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \:\alpha}−\frac{\mathrm{1}}{\mathrm{27}}}−\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}}\right) \\ $$
Commented by ajfour last updated on 16/Jan/20
Thank you Sir, but soon I am going to find a way out of this cumbersome answer.
$${Thank}\:{you}\:{Sir},\:{but}\:{soon} \\ $$$${I}\:{am}\:{going}\:{to}\:{find}\:{a}\:{way}\:{out} \\ $$$${of}\:{this}\:{cumbersome}\:{answer}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *