Question Number 7831 by Chantria last updated on 18/Sep/16
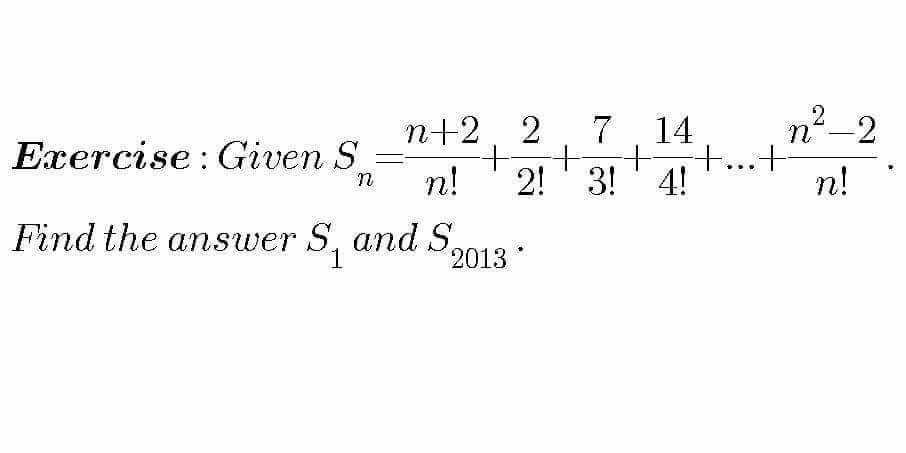
Commented by prakash jain last updated on 18/Sep/16

$${S}_{{n}} =\frac{{n}+\mathrm{2}}{{n}!}+\frac{\mathrm{2}}{{k}!}+\frac{\mathrm{7}}{{k}!}+….+\frac{{n}^{\mathrm{2}} −\mathrm{2}}{{k}!}=\frac{{n}+\mathrm{2}}{{n}!}+\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}^{\mathrm{2}} −\mathrm{2}}{{k}!} \\ $$$${n}^{\mathrm{2}} −\mathrm{2}={a}+{bn}+{cn}\left({n}−\mathrm{1}\right) \\ $$$${c}=\mathrm{1} \\ $$$${b}=\mathrm{1} \\ $$$${a}=−\mathrm{2} \\ $$$${S}_{{n}} =\frac{{n}+\mathrm{2}}{{n}!}+\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}\left({k}−\mathrm{1}\right)+{k}−\mathrm{2}}{{k}!} \\ $$$${S}_{{n}} =\frac{{n}+\mathrm{2}}{{n}!}−\frac{\mathrm{1}}{\mathrm{1}!}+\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\left({k}−\mathrm{2}\right)!}+\frac{\mathrm{1}}{\left({k}−\mathrm{1}\right)!}−\frac{\mathrm{2}}{{k}!} \\ $$$$\mathrm{T}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{0}!}+\frac{\mathrm{1}}{\mathrm{1}!}−\frac{\mathrm{2}}{\mathrm{2}!} \\ $$$$\mathrm{T}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{2}}{\mathrm{3}!} \\ $$$$\mathrm{T}_{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}−\frac{\mathrm{2}}{\mathrm{4}!} \\ $$$$\mathrm{T}_{\mathrm{5}} =\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}−\frac{\mathrm{2}}{\mathrm{5}!} \\ $$$$\mathrm{Note}:\:\mathrm{terms}\:\mathrm{in}\:\mathrm{red}\:\mathrm{and}\:\mathrm{blue}\:\mathrm{cancel}\:\mathrm{in}\:\mathrm{sum}. \\ $$$$\mathrm{T}_{\mathrm{2011}} =\frac{\mathrm{1}}{\mathrm{2009}!}+\frac{\mathrm{1}}{\mathrm{2010}!}−\frac{\mathrm{2}}{\mathrm{2011}!} \\ $$$$\mathrm{T}_{\mathrm{2012}} =\frac{\mathrm{1}}{\mathrm{2010}!}+\frac{\mathrm{1}}{\mathrm{2011}!}−\frac{\mathrm{2}}{\mathrm{2012}!} \\ $$$$\mathrm{T}_{\mathrm{2013}} =\frac{\mathrm{1}}{\mathrm{2011}!}+\frac{\mathrm{1}}{\mathrm{2012}!}−\frac{\mathrm{2}}{\mathrm{2013}!} \\ $$$$\mathrm{T}_{\mathrm{2}} +..+\mathrm{T}_{\mathrm{2013}} =\frac{\mathrm{1}}{\mathrm{0}!}+\frac{\mathrm{2}}{\mathrm{1}!}−\frac{\mathrm{1}}{\mathrm{2012}!}−\frac{\mathrm{2}}{\mathrm{2013}!} \\ $$$${S}_{\mathrm{2013}} =\frac{\mathrm{2013}+\mathrm{2}}{\mathrm{2013}!}−\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{0}!}+\frac{\mathrm{2}}{\mathrm{1}!}−\frac{\mathrm{1}}{\mathrm{2012}!}−\frac{\mathrm{2}}{\mathrm{2013}!} \\ $$$$=\frac{\mathrm{2013}+\mathrm{2}−\mathrm{2}}{\mathrm{2013}!}−\frac{\mathrm{1}}{\mathrm{2012}!}−\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{0}!}+\frac{\mathrm{2}}{\mathrm{1}!} \\ $$$$=\frac{\mathrm{2013}}{\mathrm{2013}!}−\frac{\mathrm{1}}{\mathrm{2012}!}−\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{0}!}+\frac{\mathrm{2}}{\mathrm{1}!} \\ $$$$=−\mathrm{1}+\mathrm{1}+\mathrm{2}=\mathrm{2} \\ $$
Commented by prakash jain last updated on 18/Sep/16

$$\mathrm{A}\:\mathrm{general}\:\mathrm{technique}\:\mathrm{for}\:\mathrm{solving}\:\mathrm{problem} \\ $$$$\mathrm{involving}\:\mathrm{the}\:\mathrm{following}\:\mathrm{expression} \\ $$$$\frac{{P}\left({n}\right)}{{n}!}\:\mathrm{where}\:{P}\left({n}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{polynomial}\:\mathrm{in}\:{n}\:\mathrm{of}\:\mathrm{degree}\:{k} \\ $$$$\mathrm{Write}\:{P}\left({n}\right)\:\mathrm{as} \\ $$$${P}\left({n}\right)={a}_{\mathrm{0}} +{a}_{\mathrm{1}} {n}+{a}_{\mathrm{2}} {n}\left({n}−\mathrm{1}\right)+…+{a}_{{k}} {n}\left({n}−\mathrm{1}\right)..\left({n}−{k}+\mathrm{1}\right) \\ $$$${compute}\:{a}_{\mathrm{0}} ,{a}_{\mathrm{1}} ,{a}_{\mathrm{2}} \:\mathrm{by}\:\mathrm{putting}\:{n}=\mathrm{0},\mathrm{1},\mathrm{2}\:\mathrm{etc} \\ $$$$\frac{{P}\left(\mathrm{n}\right)}{{n}!}\:\mathrm{will}\:\mathrm{simplify}\:\mathrm{to}=\frac{{a}_{\mathrm{0}} }{{n}!}+\frac{{a}_{\mathrm{1}} }{\left({n}−\mathrm{1}\right)!}+…+\frac{{a}_{{k}} }{\left({n}−{k}\right)!} \\ $$$$\mathrm{This}\:\mathrm{might}\:\mathrm{help}\:\mathrm{in}\:\mathrm{some}\:\mathrm{of}\:\mathrm{the}\:\mathrm{probelms}. \\ $$
Answered by prakash jain last updated on 02/Oct/16

$$\mathrm{see}\:\mathrm{comments} \\ $$
