Menu Close

Question-78511

Tinku Tara 0 Comments
Pin




Question Number 78511 by ajfour last updated on 18/Jan/20
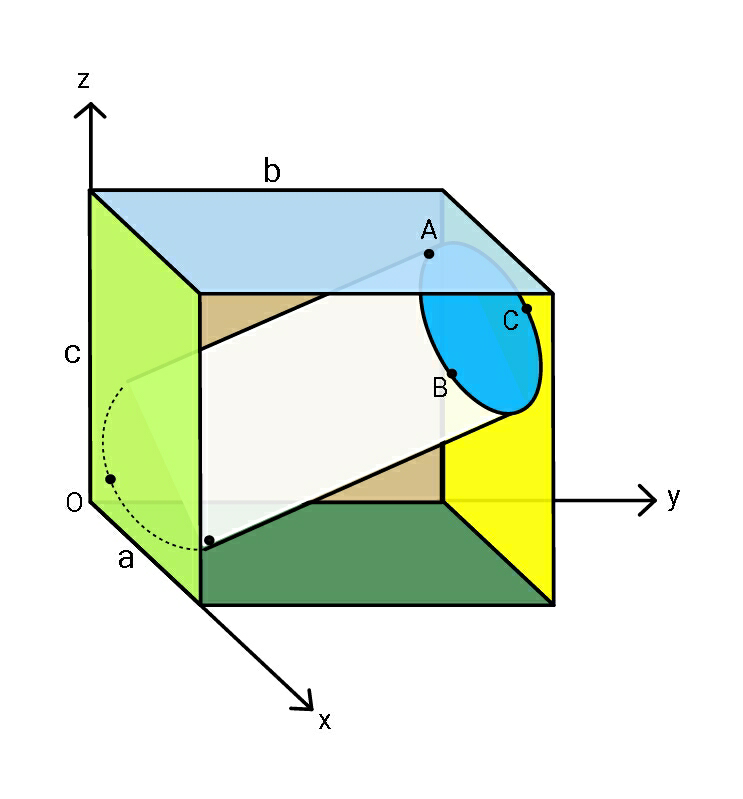
Commented by ajfour last updated on 18/Jan/20
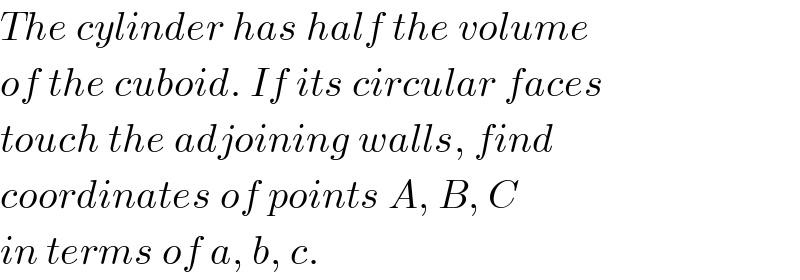
The cylinder has half the volume of the cuboid. If its circular faces touch the adjoining walls, find coordinates of points A, B, C in terms of a, b, c.
$${The}\:{cylinder}\:{has}\:{half}\:{the}\:{volume} \\ $$$${of}\:{the}\:{cuboid}.\:{If}\:{its}\:{circular}\:{faces} \\ $$$${touch}\:{the}\:{adjoining}\:{walls},\:{find} \\ $$$${coordinates}\:{of}\:{points}\:{A},\:{B},\:{C} \\ $$$${in}\:{terms}\:{of}\:{a},\:{b},\:{c}. \\ $$
Commented by ajfour last updated on 19/Jan/20
Answered by mr W last updated on 19/Jan/20
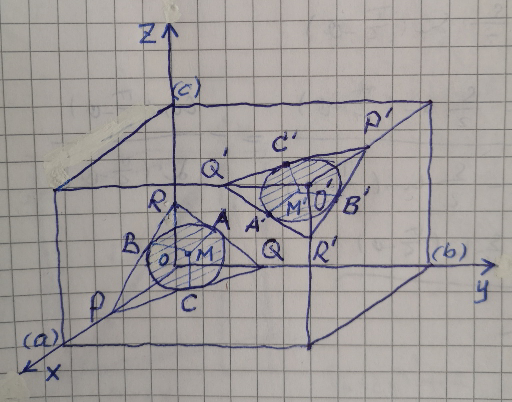
Commented by mr W last updated on 20/Jan/20
it is to find the orientation and size of the cylinder. P(α,0,0) Q(0,β,0) R(0,0,γ) P′(a−α,0,0) Q′(0,b−β,0) R′(0,0,c−γ) p=QR=(√(β^2 +γ^2 )) q=RP=(√(γ^2 +α^2 )) r=PQ=(√(α^2 +β^2 )) ρ=radius of incircle=radius of cylinder ⇒ρ=(1/2)(√(((−(√(α^2 +β^2 ))+(√(β^2 +γ^2 ))+(√(γ^2 +α^2 )))((√(α^2 +β^2 ))−(√(β^2 +γ^2 ))+(√(γ^2 +α^2 )))((√(α^2 +β^2 ))+(√(β^2 +γ^2 ))−(√(γ^2 +α^2 ))))/( (√(α^2 +β^2 ))+(√(β^2 +γ^2 ))+(√(γ^2 +α^2 ))))) M=center of incircle=axis of cylinder M=(p/(p+q+r))P+(q/(p+q+r))Q+(r/(p+q+r))R x_M =(p/(p+q+r))x_P =((α(√(β^2 +γ^2 )))/( (√(α^2 +β^2 ))+(√(β^2 +γ^2 ))+(√(γ^2 +α^2 )))) y_M =(q/(p+q+r))y_Q =((β(√(γ^2 +α^2 )))/( (√(α^2 +β^2 ))+(√(β^2 +γ^2 ))+(√(γ^2 +α^2 )))) z_M =(r/(p+q+r))z_R =((γ(√(α^2 +β^2 )))/( (√(α^2 +β^2 ))+(√(β^2 +γ^2 ))+(√(γ^2 +α^2 )))) similarly x_(M′) =(p/(p+q+r))x_(P′) =(((a−α)(√(β^2 +γ^2 )))/( (√(α^2 +β^2 ))+(√(β^2 +γ^2 ))+(√(γ^2 +α^2 )))) y_(M′) =(q/(p+q+r))y_(Q′) =(((b−β)(√(γ^2 +α^2 )))/( (√(α^2 +β^2 ))+(√(β^2 +γ^2 ))+(√(γ^2 +α^2 )))) z_(M′) =(r/(p+q+r))z_(R′) =(((c−γ)(√(α^2 +β^2 )))/( (√(α^2 +β^2 ))+(√(β^2 +γ^2 ))+(√(γ^2 +α^2 )))) Δx_(M′−M) =(((a−2α)(√(β^2 +γ^2 )))/( (√(α^2 +β^2 ))+(√(β^2 +γ^2 ))+(√(γ^2 +α^2 )))) Δy_(M′−M) =(((b−2β)(√(γ^2 +α^2 )))/( (√(α^2 +β^2 ))+(√(β^2 +γ^2 ))+(√(γ^2 +α^2 )))) Δz_(M′−M) =(((c−2γ)(√(α^2 +β^2 )))/( (√(α^2 +β^2 ))+(√(β^2 +γ^2 ))+(√(γ^2 +α^2 )))) MM′=L=((√((a−2α)^2 (β^2 +γ^2 )+(b−2β)^2 (γ^2 +α^2 )+(c−2γ)^2 (α^2 +β^2 )))/( (√(α^2 +β^2 ))+(√(β^2 +γ^2 ))+(√(γ^2 +α^2 )))) L=length of cylinder eqn. of plane PQR: (x/α)+(y/β)+(z/γ)=1 MM′⊥plane PQR: α(a−2α)(√(β^2 +γ^2 ))=β(b−2β)(√(γ^2 +α^2 ))=γ(c−2γ)(√(α^2 +β^2 )) α(a−2α)(√(β^2 +γ^2 ))=γ(c−2γ)(√(α^2 +β^2 )) ...(i) β(b−2β)(√(γ^2 +α^2 ))=γ(c−2γ)(√(α^2 +β^2 )) ...(ii) volume of cylinder V=πρ^2 L=((abc)/2) (((−(√(α^2 +β^2 ))+(√(β^2 +γ^2 ))+(√(γ^2 +α^2 )))((√(α^2 +β^2 ))−(√(β^2 +γ^2 ))+(√(γ^2 +α^2 )))((√(α^2 +β^2 ))+(√(β^2 +γ^2 ))−(√(γ^2 +α^2 )))(√((a−2α)^2 (β^2 +γ^2 )+(b−2β)^2 (γ^2 +α^2 )+(c−2γ)^2 (α^2 +β^2 ))))/(((√(α^2 +β^2 ))+(√(β^2 +γ^2 ))+(√(γ^2 +α^2 )))^2 ))=((2abc)/π) ...(iii) from (i) to (iii): α,β,γ
$${it}\:{is}\:{to}\:{find}\:{the}\:{orientation}\:{and}\:{size} \\ $$$${of}\:{the}\:{cylinder}. \\ $$$${P}\left(\alpha,\mathrm{0},\mathrm{0}\right) \\ $$$${Q}\left(\mathrm{0},\beta,\mathrm{0}\right) \\ $$$${R}\left(\mathrm{0},\mathrm{0},\gamma\right) \\ $$$${P}'\left({a}−\alpha,\mathrm{0},\mathrm{0}\right) \\ $$$${Q}'\left(\mathrm{0},{b}−\beta,\mathrm{0}\right) \\ $$$${R}'\left(\mathrm{0},\mathrm{0},{c}−\gamma\right) \\ $$$${p}={QR}=\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} } \\ $$$${q}={RP}=\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} } \\ $$$${r}={PQ}=\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} } \\ $$$$\rho={radius}\:{of}\:{incircle}={radius}\:{of}\:{cylinder} \\ $$$$\Rightarrow\rho=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\left(−\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }+\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }+\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }\right)\left(\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }−\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }+\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }\right)\left(\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }+\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }−\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }\right)}{\:\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }+\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }+\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }}} \\ $$$${M}={center}\:{of}\:{incircle}={axis}\:{of}\:{cylinder} \\ $$$$\boldsymbol{{M}}=\frac{{p}}{{p}+{q}+{r}}\boldsymbol{{P}}+\frac{{q}}{{p}+{q}+{r}}\boldsymbol{{Q}}+\frac{{r}}{{p}+{q}+{r}}\boldsymbol{{R}} \\ $$$${x}_{{M}} =\frac{{p}}{{p}+{q}+{r}}{x}_{{P}} =\frac{\alpha\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }}{\:\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }+\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }+\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }} \\ $$$${y}_{{M}} =\frac{{q}}{{p}+{q}+{r}}{y}_{{Q}} =\frac{\beta\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }}{\:\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }+\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }+\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }} \\ $$$${z}_{{M}} =\frac{{r}}{{p}+{q}+{r}}{z}_{{R}} =\frac{\gamma\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }}{\:\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }+\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }+\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }} \\ $$$${similarly} \\ $$$${x}_{{M}'} =\frac{{p}}{{p}+{q}+{r}}{x}_{{P}'} =\frac{\left({a}−\alpha\right)\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }}{\:\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }+\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }+\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }} \\ $$$${y}_{{M}'} =\frac{{q}}{{p}+{q}+{r}}{y}_{{Q}'} =\frac{\left({b}−\beta\right)\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }}{\:\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }+\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }+\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }} \\ $$$${z}_{{M}'} =\frac{{r}}{{p}+{q}+{r}}{z}_{{R}'} =\frac{\left({c}−\gamma\right)\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }}{\:\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }+\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }+\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }} \\ $$$$\Delta{x}_{{M}'−{M}} =\frac{\left({a}−\mathrm{2}\alpha\right)\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }}{\:\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }+\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }+\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }} \\ $$$$\Delta{y}_{{M}'−{M}} =\frac{\left({b}−\mathrm{2}\beta\right)\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }}{\:\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }+\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }+\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }} \\ $$$$\Delta{z}_{{M}'−{M}} =\frac{\left({c}−\mathrm{2}\gamma\right)\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }}{\:\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }+\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }+\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }} \\ $$$${MM}'={L}=\frac{\sqrt{\left({a}−\mathrm{2}\alpha\right)^{\mathrm{2}} \left(\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right)+\left({b}−\mathrm{2}\beta\right)^{\mathrm{2}} \left(\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} \right)+\left({c}−\mathrm{2}\gamma\right)^{\mathrm{2}} \left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)}}{\:\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }+\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }+\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }} \\ $$$${L}={length}\:{of}\:{cylinder} \\ $$$${eqn}.\:{of}\:{plane}\:{PQR}: \\ $$$$\frac{{x}}{\alpha}+\frac{{y}}{\beta}+\frac{{z}}{\gamma}=\mathrm{1} \\ $$$${MM}'\bot{plane}\:{PQR}: \\ $$$$\alpha\left({a}−\mathrm{2}\alpha\right)\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }=\beta\left({b}−\mathrm{2}\beta\right)\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }=\gamma\left({c}−\mathrm{2}\gamma\right)\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} } \\ $$$$\alpha\left({a}−\mathrm{2}\alpha\right)\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }=\gamma\left({c}−\mathrm{2}\gamma\right)\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }\:\:\:…\left({i}\right) \\ $$$$\beta\left({b}−\mathrm{2}\beta\right)\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }=\gamma\left({c}−\mathrm{2}\gamma\right)\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }\:\:\:…\left({ii}\right) \\ $$$${volume}\:{of}\:{cylinder}\:{V}=\pi\rho^{\mathrm{2}} {L}=\frac{{abc}}{\mathrm{2}} \\ $$$$\frac{\left(−\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }+\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }+\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }\right)\left(\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }−\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }+\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }\right)\left(\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }+\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }−\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }\right)\sqrt{\left({a}−\mathrm{2}\alpha\right)^{\mathrm{2}} \left(\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} \right)+\left({b}−\mathrm{2}\beta\right)^{\mathrm{2}} \left(\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} \right)+\left({c}−\mathrm{2}\gamma\right)^{\mathrm{2}} \left(\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \right)}}{\left(\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }+\sqrt{\beta^{\mathrm{2}} +\gamma^{\mathrm{2}} }+\sqrt{\gamma^{\mathrm{2}} +\alpha^{\mathrm{2}} }\right)^{\mathrm{2}} }=\frac{\mathrm{2}{abc}}{\pi}\:\:\:…\left({iii}\right) \\ $$$${from}\:\left({i}\right)\:{to}\:\left({iii}\right):\:\alpha,\beta,\gamma \\ $$
Commented by mr W last updated on 19/Jan/20
thank you too sir!
$${thank}\:{you}\:{too}\:{sir}! \\ $$
Commented by ajfour last updated on 19/Jan/20
Looks fabulous Sir, i shall try to follow....already i have learned somethings from your diagram post, and i am trying to solve even. Thank you immensely Sir.
$${Looks}\:{fabulous}\:{Sir},\:{i}\:{shall}\:{try} \\ $$$${to}\:{follow}….{already}\:{i}\:{have} \\ $$$${learned}\:{somethings}\:{from}\:{your} \\ $$$${diagram}\:{post},\:{and}\:{i}\:{am}\:{trying} \\ $$$${to}\:{solve}\:{even}.\:{Thank}\:{you} \\ $$$${immensely}\:{Sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *