Menu Close

Question-78549

Tinku Tara 0 Comments
Pin




Question Number 78549 by aliesam last updated on 18/Jan/20
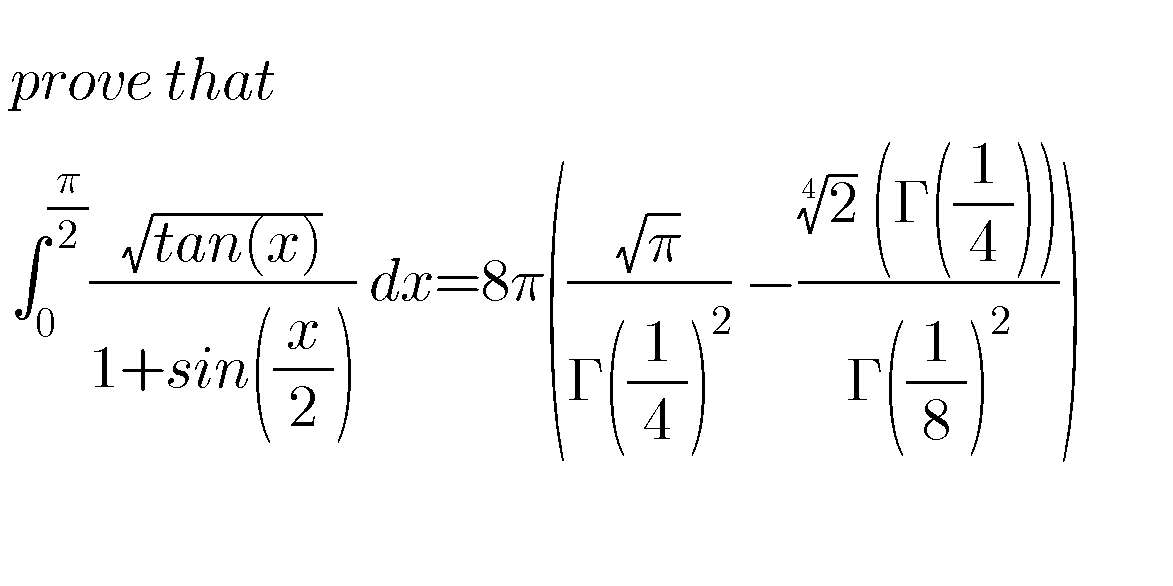
Answered by ~blr237~ last updated on 18/Jan/20
let named it A state u=(x/2) , A=2∫_0 ^(π/4) ((√(tan2u))/(1+sinu)) du (A/2)= ∫_0 ^(π/4) ((√(tan2u))/(cos^2 u))(1−sinu)du =∫_0 ^(π/4) (√(tan2u)) ((du/(cos^2 u))) −∫_0 ^(π/4) sinu(√(tan2u)) ((du/(cos^2 u))) = ∫_0 ^1 (√((2t)/(1−t^2 ))) dt − ∫_0 ^1 (√((2t^3 )/(1−t^4 ))) dt where t=tanu (A/(2(√2)))= I_2 −I_4 with I_n =∫_0 ^1 (√(t^(n−1) /(1−t^n ))) dt for n≥1 let state y=t^n ⇒ dt=(1/n)y^((1/n)−1) dy I_n = ∫_0 ^1 y^((n−1)/(2n)) (1−y)^((−1)/2) ((1/n)y^((1/n)−1) dy) nI_n =∫_0 ^1 y^((1/(2n))+(1/2)−1) (1−y)^((1/2)−1) dy =B((1/(2n))+(1/2),(1/2))=((Γ((1/(2n))+(1/2))Γ((1/2)))/(Γ((1/(2n))+1))) so I_n = ((2(√π) Γ((1/(2n))+(1/2)))/(Γ((1/(2n)))))
$$\mathrm{let}\:\mathrm{named}\:\mathrm{it}\:\mathrm{A} \\ $$$$\mathrm{state}\:\mathrm{u}=\frac{\mathrm{x}}{\mathrm{2}}\:\:,\:\mathrm{A}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\sqrt{\mathrm{tan2u}}}{\mathrm{1}+\mathrm{sinu}}\:\mathrm{du} \\ $$$$\frac{\mathrm{A}}{\mathrm{2}}=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\sqrt{\mathrm{tan2u}}}{\mathrm{cos}^{\mathrm{2}} \mathrm{u}}\left(\mathrm{1}−\mathrm{sinu}\right)\mathrm{du} \\ $$$$\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\sqrt{\mathrm{tan2u}}\:\left(\frac{\mathrm{du}}{\mathrm{cos}^{\mathrm{2}} \mathrm{u}}\right)\:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{sinu}\sqrt{\mathrm{tan2u}}\:\left(\frac{\mathrm{du}}{\mathrm{cos}^{\mathrm{2}} \mathrm{u}}\right) \\ $$$$\:\:\:\:\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\sqrt{\frac{\mathrm{2t}}{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }}\:\:\mathrm{dt}\:−\:\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\frac{\mathrm{2t}^{\mathrm{3}} }{\mathrm{1}−\mathrm{t}^{\mathrm{4}} }}\:\:\mathrm{dt}\:\:\:\:\mathrm{where}\:\mathrm{t}=\mathrm{tanu} \\ $$$$\frac{\mathrm{A}}{\mathrm{2}\sqrt{\mathrm{2}}}=\:\:\mathrm{I}_{\mathrm{2}} −\mathrm{I}_{\mathrm{4}} \:\:\:\mathrm{with}\:\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\frac{\mathrm{t}^{\mathrm{n}−\mathrm{1}} }{\mathrm{1}−\mathrm{t}^{\mathrm{n}} }}\:\mathrm{dt}\:\:\mathrm{for}\:\mathrm{n}\geqslant\mathrm{1}\: \\ $$$$\mathrm{let}\:\mathrm{state}\:\:\mathrm{y}=\mathrm{t}^{\mathrm{n}} \:\:\:\Rightarrow\:\mathrm{dt}=\frac{\mathrm{1}}{\mathrm{n}}\mathrm{y}^{\frac{\mathrm{1}}{\mathrm{n}}−\mathrm{1}} \mathrm{dy} \\ $$$$\mathrm{I}_{\mathrm{n}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{y}^{\frac{\mathrm{n}−\mathrm{1}}{\mathrm{2n}}} \left(\mathrm{1}−\mathrm{y}\right)^{\frac{−\mathrm{1}}{\mathrm{2}}} \left(\frac{\mathrm{1}}{\mathrm{n}}\mathrm{y}^{\frac{\mathrm{1}}{\mathrm{n}}−\mathrm{1}} \mathrm{dy}\right) \\ $$$$\:\mathrm{nI}_{\mathrm{n}} \:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{y}^{\frac{\mathrm{1}}{\mathrm{2n}}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \left(\mathrm{1}−\mathrm{y}\right)^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \mathrm{dy} \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{B}\left(\frac{\mathrm{1}}{\mathrm{2n}}+\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2n}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2n}}+\mathrm{1}\right)}\: \\ $$$$\:\:\mathrm{so}\:\:\mathrm{I}_{\mathrm{n}} =\:\frac{\mathrm{2}\sqrt{\pi}\:\Gamma\left(\frac{\mathrm{1}}{\mathrm{2n}}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2n}}\right)} \\ $$$$ \\ $$
Commented by mind is power last updated on 19/Jan/20
nice Sir
$$\mathrm{nice}\:\mathrm{Sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *