Question Number 7855 by 314159 last updated on 21/Sep/16

Commented by 123456 last updated on 21/Sep/16
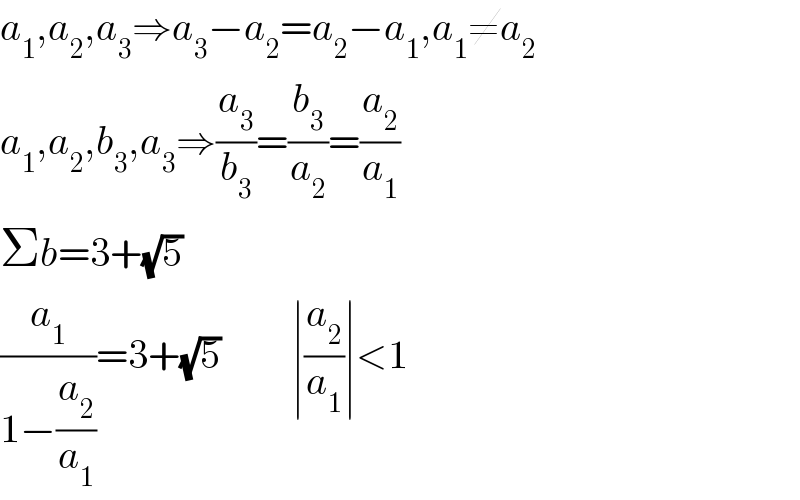
$${a}_{\mathrm{1}} ,{a}_{\mathrm{2}} ,{a}_{\mathrm{3}} \Rightarrow{a}_{\mathrm{3}} −{a}_{\mathrm{2}} ={a}_{\mathrm{2}} −{a}_{\mathrm{1}} ,{a}_{\mathrm{1}} \neq{a}_{\mathrm{2}} \\ $$$${a}_{\mathrm{1}} ,{a}_{\mathrm{2}} ,{b}_{\mathrm{3}} ,{a}_{\mathrm{3}} \Rightarrow\frac{{a}_{\mathrm{3}} }{{b}_{\mathrm{3}} }=\frac{{b}_{\mathrm{3}} }{{a}_{\mathrm{2}} }=\frac{{a}_{\mathrm{2}} }{{a}_{\mathrm{1}} } \\ $$$$\Sigma{b}=\mathrm{3}+\sqrt{\mathrm{5}} \\ $$$$\frac{{a}_{\mathrm{1}} }{\mathrm{1}−\frac{{a}_{\mathrm{2}} }{{a}_{\mathrm{1}} }}=\mathrm{3}+\sqrt{\mathrm{5}}\:\:\:\:\:\:\:\:\:\mid\frac{{a}_{\mathrm{2}} }{{a}_{\mathrm{1}} }\mid<\mathrm{1} \\ $$
Commented by Rasheed Soomro last updated on 21/Sep/16
![a,ar,ar^2 ,ar^3 ,...[a:first term,r:common ratio] a,ar,ar^3 are in AP, ar is AM between a and ar^3 ∴ ar=((a+ar^3 )/2)⇒2r=1+r^3 ⇒r^3 −2r+1=0 S=(a/(1−r))=3+(√5) [S =a+ar+ar^2 +...]..........(∗) An attempt to factrize r^3 −2r+1 r^3 −2r+1=0 2r^3 −2r+1−r^3 =0 2r(r^2 −1)−(r^3 −1)=0 2r(r−1)(r+1)−(r−1)(r^2 +r+1)=0 (r−1)[2r(r+1)−(r^2 +r+1)]=0 r−1=0 ∣ 2r^2 +2r−r^2 −r−1=0 r=1 ∣ r^2 +r−1=0 r=1 is discardable because S is infinity there. So r^2 +r−1=0 [r≠1] r=((−1±(√(1+4)))/2)=((1±(√5))/2) As r<1 So as ((1+(√5))/2)>0, Hence r= ((1−(√5))/2) is the only value. From (∗) (a/(1−r))=3+(√5) a=(3+(√5))(1−r) a=(3+(√5))(1−((1−(√5))/2)) a=(3+(√5))(((2−1+(√5))/2))=(3+(√5))(((1+(√5))/2)) a=(((3+(√5))(1+(√5)))/2) a=((3+3(√5)+(√5)+5)/2) =4+2(√5) So the first term is 4+2(√5)](https://www.tinkutara.com/question/Q7857.png)
$${a},{ar},{ar}^{\mathrm{2}} ,{ar}^{\mathrm{3}} ,…\left[{a}:{first}\:{term},{r}:{common}\:{ratio}\right] \\ $$$${a},{ar},{ar}^{\mathrm{3}} \:\:\:{are}\:{in}\:{AP},\:{ar}\:{is}\:{AM}\:{between}\:{a}\:{and}\:{ar}^{\mathrm{3}} \\ $$$$\therefore\:{ar}=\frac{{a}+{ar}^{\mathrm{3}} }{\mathrm{2}}\Rightarrow\mathrm{2}{r}=\mathrm{1}+{r}^{\mathrm{3}} \Rightarrow{r}^{\mathrm{3}} −\mathrm{2}{r}+\mathrm{1}=\mathrm{0} \\ $$$${S}=\frac{{a}}{\mathrm{1}−{r}}=\mathrm{3}+\sqrt{\mathrm{5}}\:\:\:\left[{S}\:={a}+{ar}+{ar}^{\mathrm{2}} +…\right]……….\left(\ast\right) \\ $$$${An}\:{attempt}\:{to}\:{factrize}\:{r}^{\mathrm{3}} −\mathrm{2}{r}+\mathrm{1} \\ $$$${r}^{\mathrm{3}} −\mathrm{2}{r}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{2}{r}^{\mathrm{3}} −\mathrm{2}{r}+\mathrm{1}−{r}^{\mathrm{3}} =\mathrm{0} \\ $$$$\mathrm{2}{r}\left({r}^{\mathrm{2}} −\mathrm{1}\right)−\left({r}^{\mathrm{3}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{2}{r}\left({r}−\mathrm{1}\right)\left({r}+\mathrm{1}\right)−\left({r}−\mathrm{1}\right)\left({r}^{\mathrm{2}} +{r}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({r}−\mathrm{1}\right)\left[\mathrm{2}{r}\left({r}+\mathrm{1}\right)−\left({r}^{\mathrm{2}} +{r}+\mathrm{1}\right)\right]=\mathrm{0} \\ $$$${r}−\mathrm{1}=\mathrm{0}\:\:\:\:\mid\:\:\mathrm{2}{r}^{\mathrm{2}} +\mathrm{2}{r}−{r}^{\mathrm{2}} −{r}−\mathrm{1}=\mathrm{0} \\ $$$$\:{r}=\mathrm{1}\:\:\:\:\:\:\:\:\:\:\mid\:\:\:\:{r}^{\mathrm{2}} +{r}−\mathrm{1}=\mathrm{0} \\ $$$${r}=\mathrm{1}\:{is}\:{discardable}\:{because}\:{S}\:{is}\:{infinity}\:{there}. \\ $$$${So}\:\:\:\:\:\:{r}^{\mathrm{2}} +{r}−\mathrm{1}=\mathrm{0}\:\:\:\left[{r}\neq\mathrm{1}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{r}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{4}}}{\mathrm{2}}=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${As}\:{r}<\mathrm{1}\:{So}\:{as}\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}>\mathrm{0},\:\:{Hence}\:{r}=\:\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\:{is}\:{the}\:{only}\:{value}. \\ $$$${From}\:\:\:\left(\ast\right) \\ $$$$\:\:\:\:\:\:\:\:\:\frac{{a}}{\mathrm{1}−{r}}=\mathrm{3}+\sqrt{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\:{a}=\left(\mathrm{3}+\sqrt{\mathrm{5}}\right)\left(\mathrm{1}−{r}\right) \\ $$$$\:\:\:\:\:\:\:\:{a}=\left(\mathrm{3}+\sqrt{\mathrm{5}}\right)\left(\mathrm{1}−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:{a}=\left(\mathrm{3}+\sqrt{\mathrm{5}}\right)\left(\frac{\mathrm{2}−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)=\left(\mathrm{3}+\sqrt{\mathrm{5}}\right)\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$$$\:{a}=\frac{\left(\mathrm{3}+\sqrt{\mathrm{5}}\right)\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)}{\mathrm{2}} \\ $$$$\:\:\:\:{a}=\frac{\mathrm{3}+\mathrm{3}\sqrt{\mathrm{5}}+\sqrt{\mathrm{5}}+\mathrm{5}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{4}+\mathrm{2}\sqrt{\mathrm{5}} \\ $$$${So}\:{the}\:{first}\:{term}\:{is}\:\:\mathrm{4}+\mathrm{2}\sqrt{\mathrm{5}} \\ $$$$\:\:\:\:\:\: \\ $$
Commented by 314159 last updated on 22/Sep/16

$$\boldsymbol{\mathrm{Thank}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{lot}}! \\ $$
Commented by lepan last updated on 06/Oct/16

$${a}=−\mathrm{1}−\sqrt{\mathrm{5}} \\ $$
