Question Number 8373 by arinto27 last updated on 09/Oct/16
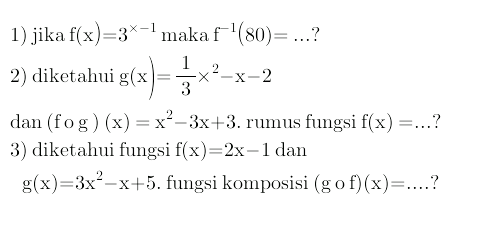
Commented by ridwan balatif last updated on 09/Oct/16
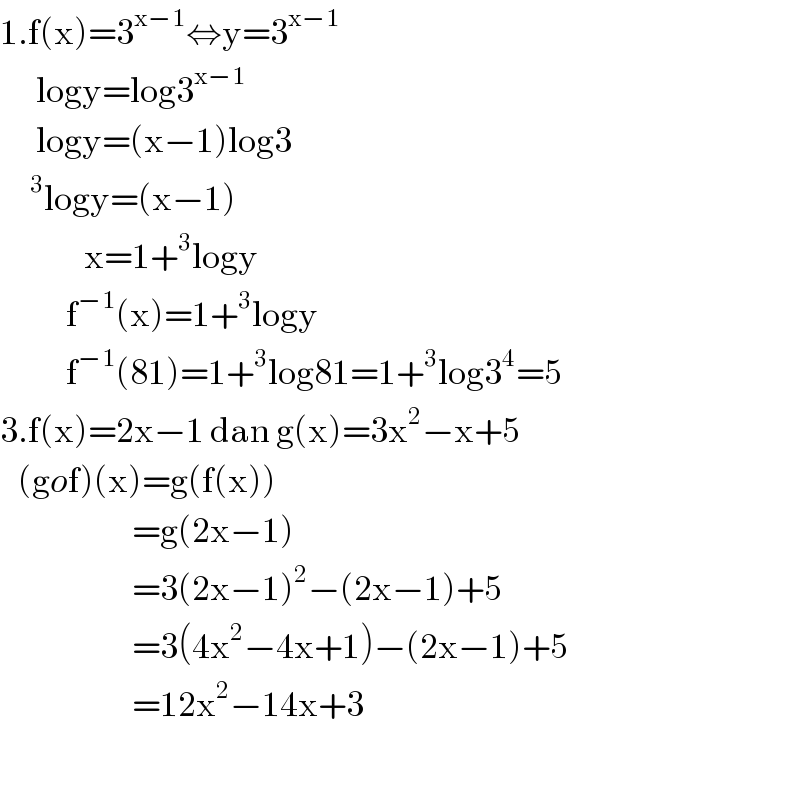
$$\mathrm{1}.\mathrm{f}\left(\mathrm{x}\right)=\mathrm{3}^{\mathrm{x}−\mathrm{1}} \Leftrightarrow\mathrm{y}=\mathrm{3}^{\mathrm{x}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\mathrm{logy}=\mathrm{log3}^{\mathrm{x}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\mathrm{logy}=\left(\mathrm{x}−\mathrm{1}\right)\mathrm{log3} \\ $$$$\:\:\:\:\:^{\mathrm{3}} \mathrm{logy}=\left(\mathrm{x}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}=\mathrm{1}+^{\mathrm{3}} \mathrm{logy} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}\right)=\mathrm{1}+^{\mathrm{3}} \mathrm{logy} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{f}^{−\mathrm{1}} \left(\mathrm{81}\right)=\mathrm{1}+^{\mathrm{3}} \mathrm{log81}=\mathrm{1}+^{\mathrm{3}} \mathrm{log3}^{\mathrm{4}} =\mathrm{5} \\ $$$$\mathrm{3}.\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2x}−\mathrm{1}\:\mathrm{dan}\:\mathrm{g}\left(\mathrm{x}\right)=\mathrm{3x}^{\mathrm{2}} −\mathrm{x}+\mathrm{5} \\ $$$$\:\:\:\left(\mathrm{g}{o}\mathrm{f}\right)\left(\mathrm{x}\right)=\mathrm{g}\left(\mathrm{f}\left(\mathrm{x}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{g}\left(\mathrm{2x}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{3}\left(\mathrm{2x}−\mathrm{1}\right)^{\mathrm{2}} −\left(\mathrm{2x}−\mathrm{1}\right)+\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{3}\left(\mathrm{4x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{1}\right)−\left(\mathrm{2x}−\mathrm{1}\right)+\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{12x}^{\mathrm{2}} −\mathrm{14x}+\mathrm{3} \\ $$$$ \\ $$
Commented by sandy_suhendra last updated on 09/Oct/16
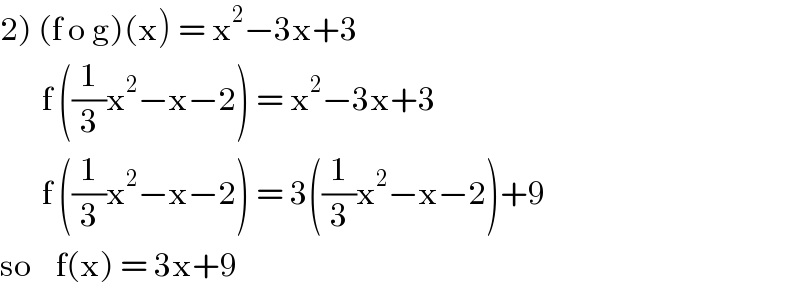
$$\left.\mathrm{2}\right)\:\left(\mathrm{f}\:\mathrm{o}\:\mathrm{g}\right)\left(\mathrm{x}\right)\:=\:\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\mathrm{f}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{2}\right)\:=\:\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\mathrm{f}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{2}\right)\:=\:\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{2}\right)+\mathrm{9} \\ $$$$\mathrm{so}\:\:\:\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{3x}+\mathrm{9} \\ $$
Answered by ridwan balatif last updated on 09/Oct/16
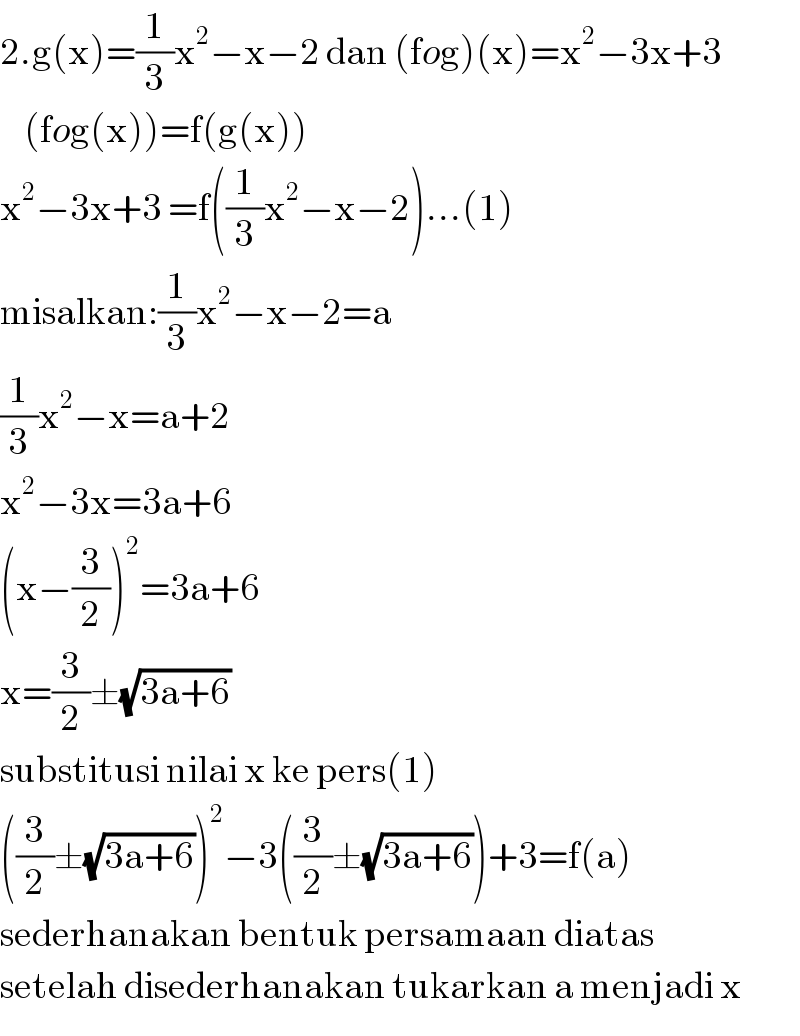
$$\mathrm{2}.\mathrm{g}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{2}\:\mathrm{dan}\:\left(\mathrm{f}{o}\mathrm{g}\right)\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{3} \\ $$$$\:\:\:\:\left(\mathrm{f}{o}\mathrm{g}\left(\mathrm{x}\right)\right)=\mathrm{f}\left(\mathrm{g}\left(\mathrm{x}\right)\right) \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{3}\:=\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{2}\right)…\left(\mathrm{1}\right) \\ $$$$\mathrm{misalkan}:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{2}} −\mathrm{x}−\mathrm{2}=\mathrm{a} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{2}} −\mathrm{x}=\mathrm{a}+\mathrm{2} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{3x}=\mathrm{3a}+\mathrm{6} \\ $$$$\left(\mathrm{x}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{3a}+\mathrm{6} \\ $$$$\mathrm{x}=\frac{\mathrm{3}}{\mathrm{2}}\pm\sqrt{\mathrm{3a}+\mathrm{6}} \\ $$$$\mathrm{substitusi}\:\mathrm{nilai}\:\mathrm{x}\:\mathrm{ke}\:\mathrm{pers}\left(\mathrm{1}\right) \\ $$$$\left(\frac{\mathrm{3}}{\mathrm{2}}\pm\sqrt{\mathrm{3a}+\mathrm{6}}\right)^{\mathrm{2}} −\mathrm{3}\left(\frac{\mathrm{3}}{\mathrm{2}}\pm\sqrt{\mathrm{3a}+\mathrm{6}}\right)+\mathrm{3}=\mathrm{f}\left(\mathrm{a}\right) \\ $$$$\mathrm{sederhanakan}\:\mathrm{bentuk}\:\mathrm{persamaan}\:\mathrm{diatas} \\ $$$$\mathrm{setelah}\:\mathrm{disederhanakan}\:\mathrm{tukarkan}\:\mathrm{a}\:\mathrm{menjadi}\:\mathrm{x} \\ $$
