Menu Close

Question-8452

Tinku Tara 0 Comments
Pin




Question Number 8452 by tawakalitu last updated on 11/Oct/16
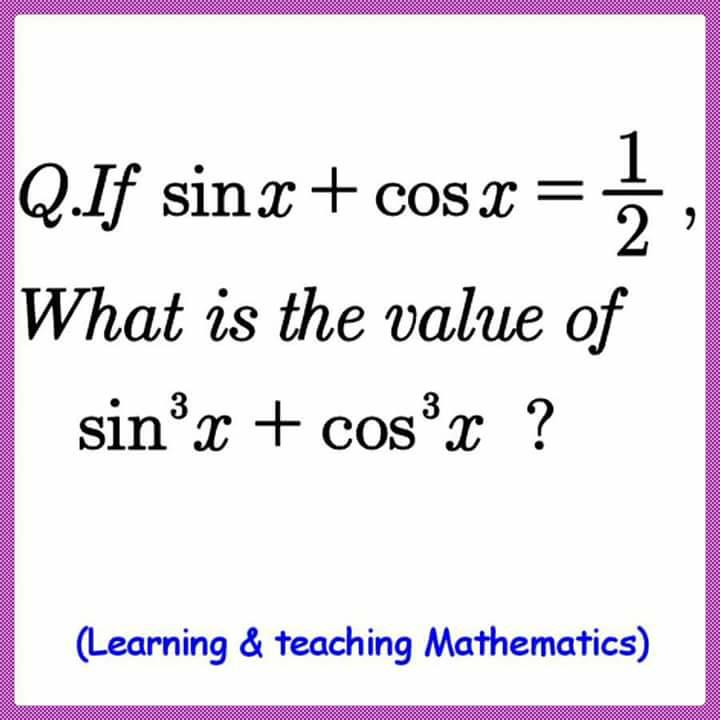
Commented by 123456 last updated on 12/Oct/16
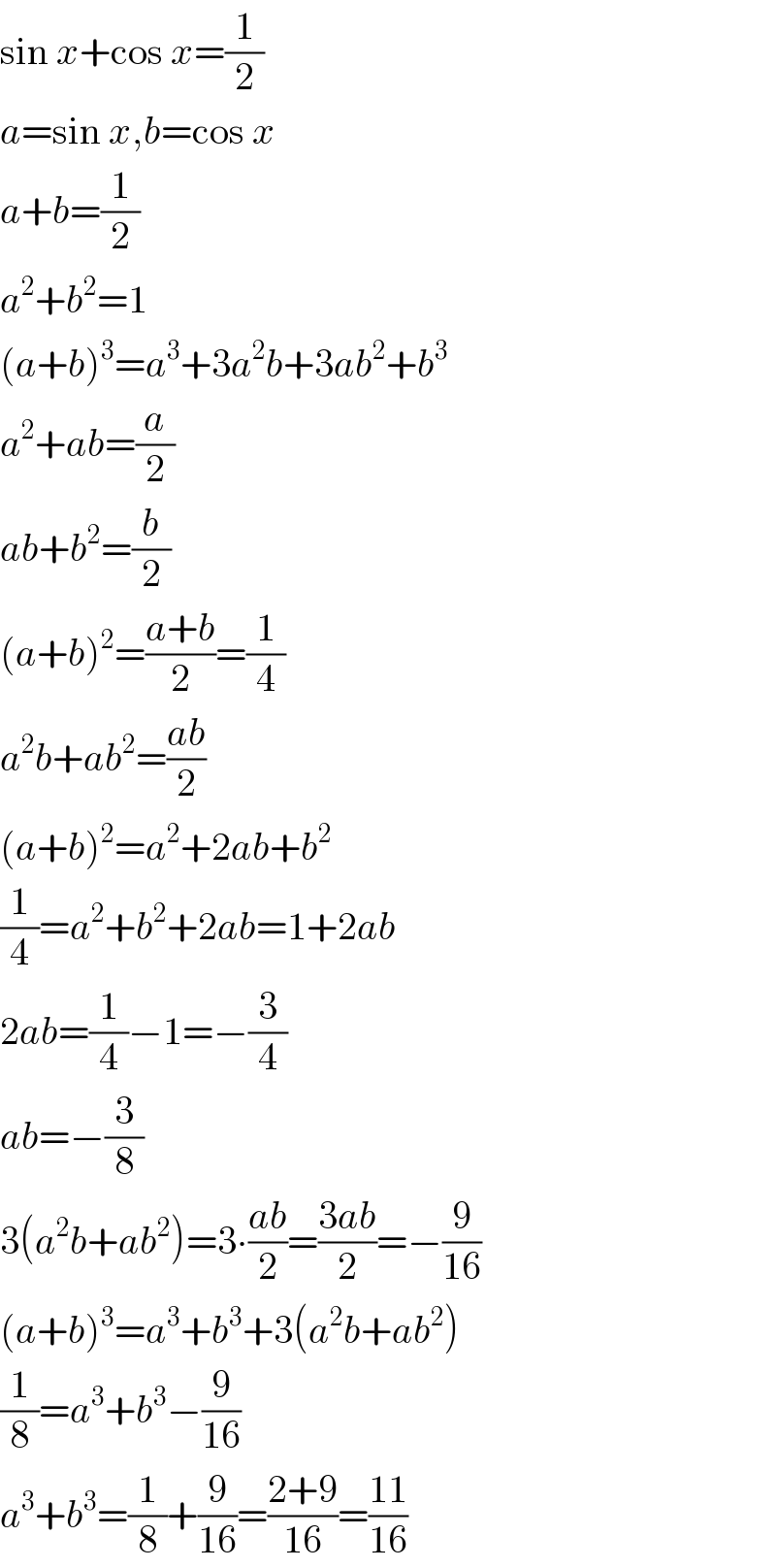
sin x+cos x=(1/2) a=sin x,b=cos x a+b=(1/2) a^2 +b^2 =1 (a+b)^3 =a^3 +3a^2 b+3ab^2 +b^3 a^2 +ab=(a/2) ab+b^2 =(b/2) (a+b)^2 =((a+b)/2)=(1/4) a^2 b+ab^2 =((ab)/2) (a+b)^2 =a^2 +2ab+b^2 (1/4)=a^2 +b^2 +2ab=1+2ab 2ab=(1/4)−1=−(3/4) ab=−(3/8) 3(a^2 b+ab^2 )=3∙((ab)/2)=((3ab)/2)=−(9/(16)) (a+b)^3 =a^3 +b^3 +3(a^2 b+ab^2 ) (1/8)=a^3 +b^3 −(9/(16)) a^3 +b^3 =(1/8)+(9/(16))=((2+9)/(16))=((11)/(16))
$$\mathrm{sin}\:{x}+\mathrm{cos}\:{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${a}=\mathrm{sin}\:{x},{b}=\mathrm{cos}\:{x} \\ $$$${a}+{b}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{1} \\ $$$$\left({a}+{b}\right)^{\mathrm{3}} ={a}^{\mathrm{3}} +\mathrm{3}{a}^{\mathrm{2}} {b}+\mathrm{3}{ab}^{\mathrm{2}} +{b}^{\mathrm{3}} \\ $$$${a}^{\mathrm{2}} +{ab}=\frac{{a}}{\mathrm{2}} \\ $$$${ab}+{b}^{\mathrm{2}} =\frac{{b}}{\mathrm{2}} \\ $$$$\left({a}+{b}\right)^{\mathrm{2}} =\frac{{a}+{b}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${a}^{\mathrm{2}} {b}+{ab}^{\mathrm{2}} =\frac{{ab}}{\mathrm{2}} \\ $$$$\left({a}+{b}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +\mathrm{2}{ab}+{b}^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}=\mathrm{1}+\mathrm{2}{ab} \\ $$$$\mathrm{2}{ab}=\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}=−\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${ab}=−\frac{\mathrm{3}}{\mathrm{8}} \\ $$$$\mathrm{3}\left({a}^{\mathrm{2}} {b}+{ab}^{\mathrm{2}} \right)=\mathrm{3}\centerdot\frac{{ab}}{\mathrm{2}}=\frac{\mathrm{3}{ab}}{\mathrm{2}}=−\frac{\mathrm{9}}{\mathrm{16}} \\ $$$$\left({a}+{b}\right)^{\mathrm{3}} ={a}^{\mathrm{3}} +{b}^{\mathrm{3}} +\mathrm{3}\left({a}^{\mathrm{2}} {b}+{ab}^{\mathrm{2}} \right) \\ $$$$\frac{\mathrm{1}}{\mathrm{8}}={a}^{\mathrm{3}} +{b}^{\mathrm{3}} −\frac{\mathrm{9}}{\mathrm{16}} \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{9}}{\mathrm{16}}=\frac{\mathrm{2}+\mathrm{9}}{\mathrm{16}}=\frac{\mathrm{11}}{\mathrm{16}} \\ $$
Commented by ridwan balatif last updated on 12/Oct/16
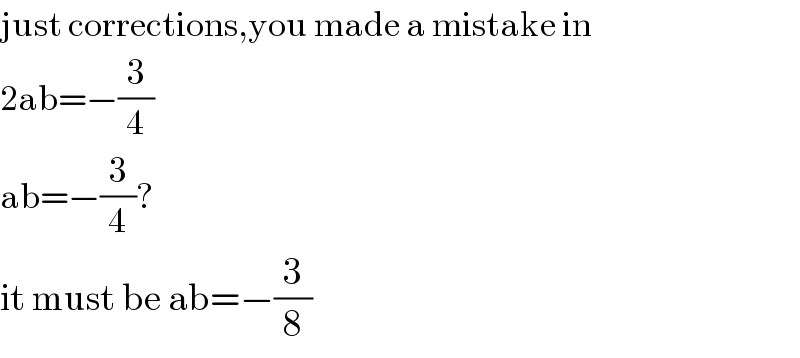
just corrections,you made a mistake in 2ab=−(3/4) ab=−(3/4)? it must be ab=−(3/8)
$$\mathrm{just}\:\mathrm{corrections},\mathrm{you}\:\mathrm{made}\:\mathrm{a}\:\mathrm{mistake}\:\mathrm{in} \\ $$$$\mathrm{2ab}=−\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{ab}=−\frac{\mathrm{3}}{\mathrm{4}}?\: \\ $$$$\mathrm{it}\:\mathrm{must}\:\mathrm{be}\:\mathrm{ab}=−\frac{\mathrm{3}}{\mathrm{8}} \\ $$
Commented by tawakalitu last updated on 12/Oct/16
Thanks so much.
$$\mathrm{Thanks}\:\mathrm{so}\:\mathrm{much}. \\ $$
Answered by ridwan balatif last updated on 12/Oct/16
sinx+cosx=(1/2), sin^3 x+cos^3 x=...? (sinx+cosx)^2 =((1/2))^2 sin^2 x+cos^2 x+2sinxcosx=(1/4) 1+2sinxcosx=(1/4) sinxcosx=−(3/8) sin^3 x+cos^3 x=(sinx+cosx)^3 −3sinxcosx(sinx+cosx) =((1/2))^3 −3×(((−3)/8))×((1/2)) =(1/8)+(9/(16)) =((11)/(16)) OR sin^3 x+cos^3 x=(sinx+cosx)(sin^2 x−sinxcosx+cos^2 x) =((1/2))(1−(−(3/8))) =((1/2))(((11)/8)) =((11)/(16))
$$\mathrm{sinx}+\mathrm{cosx}=\frac{\mathrm{1}}{\mathrm{2}},\:\:\mathrm{sin}^{\mathrm{3}} \mathrm{x}+\mathrm{cos}^{\mathrm{3}} \mathrm{x}=…? \\ $$$$\left(\mathrm{sinx}+\mathrm{cosx}\right)^{\mathrm{2}} =\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{sin}^{\mathrm{2}} \mathrm{x}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{2sinxcosx}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{1}+\mathrm{2sinxcosx}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{sinxcosx}=−\frac{\mathrm{3}}{\mathrm{8}} \\ $$$$\mathrm{sin}^{\mathrm{3}} \mathrm{x}+\mathrm{cos}^{\mathrm{3}} \mathrm{x}=\left(\mathrm{sinx}+\mathrm{cosx}\right)^{\mathrm{3}} −\mathrm{3sinxcosx}\left(\mathrm{sinx}+\mathrm{cosx}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} −\mathrm{3}×\left(\frac{−\mathrm{3}}{\mathrm{8}}\right)×\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{9}}{\mathrm{16}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{11}}{\mathrm{16}} \\ $$$$\:\mathrm{OR} \\ $$$$\mathrm{sin}^{\mathrm{3}} \mathrm{x}+\mathrm{cos}^{\mathrm{3}} \mathrm{x}=\left(\mathrm{sinx}+\mathrm{cosx}\right)\left(\mathrm{sin}^{\mathrm{2}} \mathrm{x}−\mathrm{sinxcosx}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}−\left(−\frac{\mathrm{3}}{\mathrm{8}}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\frac{\mathrm{11}}{\mathrm{8}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{11}}{\mathrm{16}} \\ $$
Commented by tawakalitu last updated on 12/Oct/16
Thanks so much.
$$\mathrm{Thanks}\:\mathrm{so}\:\mathrm{much}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *