Question Number 8517 by Chantria last updated on 14/Oct/16
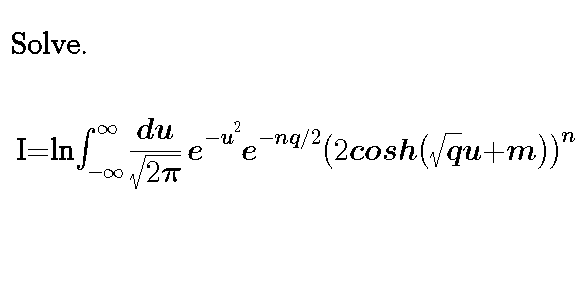
Commented by prakash jain last updated on 14/Oct/16

$${n}\:+\mathrm{ve}\:\mathrm{integer}? \\ $$
Commented by Yozzias last updated on 15/Oct/16
![I=ln[(1/( (√(2π))))2^n e^(−nq/2) ∫_(−∞) ^∞ e^(−u^2 ) cosh^n ((√q)u+m)du] I=ln[(1/( (√(2π))))2^(n+1) e^(−nq/2) ∫_0 ^∞ e^(−u^2 ) cosh^n ((√q)u+m)du]](https://www.tinkutara.com/question/Q8548.png)
$$\mathrm{I}=\mathrm{ln}\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}\pi}}\mathrm{2}^{\mathrm{n}} \mathrm{e}^{−\mathrm{nq}/\mathrm{2}} \underset{−\infty} {\overset{\infty} {\int}}\mathrm{e}^{−\mathrm{u}^{\mathrm{2}} } \mathrm{cosh}^{\mathrm{n}} \left(\sqrt{\mathrm{q}}\mathrm{u}+\mathrm{m}\right)\mathrm{du}\right] \\ $$$$\mathrm{I}=\mathrm{ln}\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}\pi}}\mathrm{2}^{\mathrm{n}+\mathrm{1}} \mathrm{e}^{−\mathrm{nq}/\mathrm{2}} \underset{\mathrm{0}} {\overset{\infty} {\int}}\mathrm{e}^{−\mathrm{u}^{\mathrm{2}} } \mathrm{cosh}^{\mathrm{n}} \left(\sqrt{\mathrm{q}}\mathrm{u}+\mathrm{m}\right)\mathrm{du}\right] \\ $$$$ \\ $$
