Menu Close

Question-8550

Tinku Tara 0 Comments
Pin




Question Number 8550 by tawakalitu last updated on 15/Oct/16
Answered by ridwan balatif last updated on 16/Oct/16
Commented by tawakalitu last updated on 16/Oct/16
Wow. God bless you sir.
$$\mathrm{Wow}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by sandy_suhendra last updated on 16/Oct/16
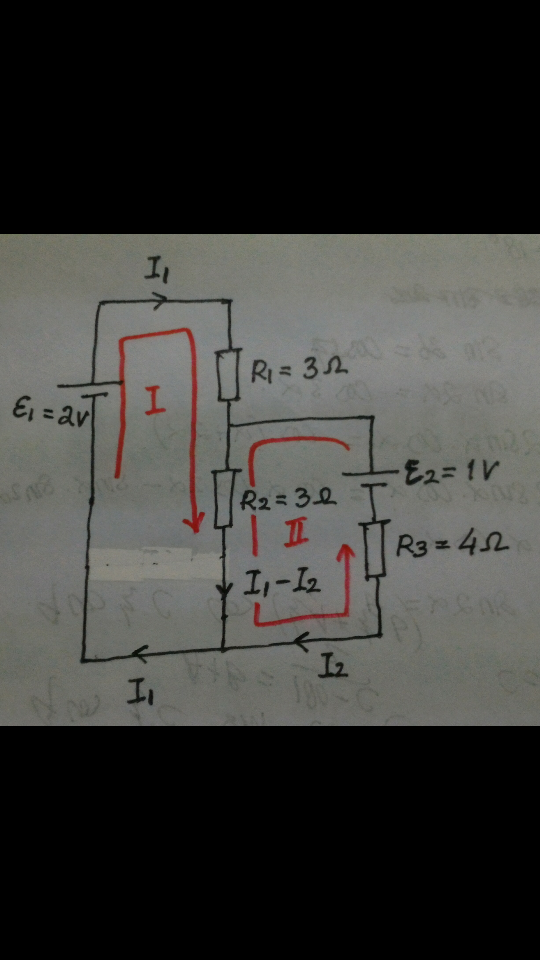
Commented by sandy_suhendra last updated on 16/Oct/16
answer for pic A loop 1 ⇒ ΣE + ΣI.R=0 −E_1 +I_1 .R_1 +(I_1 −I_2 ).R_2 =0 −2+3I_1 +(I_1 −I_2 ).3 =0 3I_1 +3I_1 −3I_2 =2 6I_1 −3I_2 =2 .....(1) loop 2 ⇒ ΣE+ΣI.R=0 −E_2 +(I_1 −I_2 ).R_2 −I_2 .R_3 =0 −1+(I_1 −I_2 ).3−4I_2 =0 3I_1 −3I_2 −4I_2 =1 3I_1 −7I_2 =1 .....(2) (1)−2×(2) ⇒ 11I_2 =1 I_2 =(1/(11)) A subs to (1) we get ⇒ I_1 =(6/(11)) A ΔV at R_1 =I_1 .R_1 =(6/(11))×3=((18)/(11)) volt P at R_1 =ΔV.I_1 =((18)/(11))×(6/(11))=((108)/(121)) watt ΔV at R_2 =(I_1 −I_2 ).R_2 =((6/(11))−(1/(11)))×3=((15)/(11)) volt P at R_2 =ΔV.(I_1 −I_2 )=((15)/(11))×(5/(11))=((75)/(121)) watt ΔV at R_3 =I_2 .R_3 =(1/(11))×4=(4/(11)) volt P at R_3 =ΔV.I_2 =(4/(11))×(1/(11))=(4/(121)) watt
$$\mathrm{answer}\:\mathrm{for}\:\mathrm{pic}\:\mathrm{A} \\ $$$$\mathrm{loop}\:\mathrm{1}\:\Rightarrow\:\Sigma\mathrm{E}\:+\:\Sigma\mathrm{I}.\mathrm{R}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{E}_{\mathrm{1}} +\mathrm{I}_{\mathrm{1}} .\mathrm{R}_{\mathrm{1}} +\left(\mathrm{I}_{\mathrm{1}} −\mathrm{I}_{\mathrm{2}} \right).\mathrm{R}_{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2}+\mathrm{3I}_{\mathrm{1}} +\left(\mathrm{I}_{\mathrm{1}} −\mathrm{I}_{\mathrm{2}} \right).\mathrm{3}\:=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3I}_{\mathrm{1}} +\mathrm{3I}_{\mathrm{1}} −\mathrm{3I}_{\mathrm{2}} =\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{6I}_{\mathrm{1}} −\mathrm{3I}_{\mathrm{2}} =\mathrm{2}\:…..\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{loop}\:\mathrm{2}\:\Rightarrow\:\Sigma\mathrm{E}+\Sigma\mathrm{I}.\mathrm{R}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{E}_{\mathrm{2}} +\left(\mathrm{I}_{\mathrm{1}} −\mathrm{I}_{\mathrm{2}} \right).\mathrm{R}_{\mathrm{2}} −\mathrm{I}_{\mathrm{2}} .\mathrm{R}_{\mathrm{3}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{1}+\left(\mathrm{I}_{\mathrm{1}} −\mathrm{I}_{\mathrm{2}} \right).\mathrm{3}−\mathrm{4I}_{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3I}_{\mathrm{1}} −\mathrm{3I}_{\mathrm{2}} −\mathrm{4I}_{\mathrm{2}} =\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3I}_{\mathrm{1}} −\mathrm{7I}_{\mathrm{2}} =\mathrm{1}\:…..\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)−\mathrm{2}×\left(\mathrm{2}\right)\:\Rightarrow\:\mathrm{11I}_{\mathrm{2}} =\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{11}}\:\mathrm{A}\:\:\mathrm{subs}\:\mathrm{to}\:\left(\mathrm{1}\right) \\ $$$$\mathrm{we}\:\mathrm{get}\:\Rightarrow\:\mathrm{I}_{\mathrm{1}} =\frac{\mathrm{6}}{\mathrm{11}}\:\mathrm{A} \\ $$$$\Delta\mathrm{V}\:\mathrm{at}\:\mathrm{R}_{\mathrm{1}} =\mathrm{I}_{\mathrm{1}} .\mathrm{R}_{\mathrm{1}} =\frac{\mathrm{6}}{\mathrm{11}}×\mathrm{3}=\frac{\mathrm{18}}{\mathrm{11}}\:\mathrm{volt} \\ $$$$\mathrm{P}\:\mathrm{at}\:\mathrm{R}_{\mathrm{1}} =\Delta\mathrm{V}.\mathrm{I}_{\mathrm{1}} =\frac{\mathrm{18}}{\mathrm{11}}×\frac{\mathrm{6}}{\mathrm{11}}=\frac{\mathrm{108}}{\mathrm{121}}\:\mathrm{watt} \\ $$$$\Delta\mathrm{V}\:\mathrm{at}\:\mathrm{R}_{\mathrm{2}} =\left(\mathrm{I}_{\mathrm{1}} −\mathrm{I}_{\mathrm{2}} \right).\mathrm{R}_{\mathrm{2}} =\left(\frac{\mathrm{6}}{\mathrm{11}}−\frac{\mathrm{1}}{\mathrm{11}}\right)×\mathrm{3}=\frac{\mathrm{15}}{\mathrm{11}}\:\mathrm{volt} \\ $$$$\mathrm{P}\:\mathrm{at}\:\mathrm{R}_{\mathrm{2}} =\Delta\mathrm{V}.\left(\mathrm{I}_{\mathrm{1}} −\mathrm{I}_{\mathrm{2}} \right)=\frac{\mathrm{15}}{\mathrm{11}}×\frac{\mathrm{5}}{\mathrm{11}}=\frac{\mathrm{75}}{\mathrm{121}}\:\mathrm{watt} \\ $$$$\Delta\mathrm{V}\:\mathrm{at}\:\mathrm{R}_{\mathrm{3}} =\mathrm{I}_{\mathrm{2}} .\mathrm{R}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{11}}×\mathrm{4}=\frac{\mathrm{4}}{\mathrm{11}}\:\mathrm{volt} \\ $$$$\mathrm{P}\:\mathrm{at}\:\mathrm{R}_{\mathrm{3}} =\Delta\mathrm{V}.\mathrm{I}_{\mathrm{2}} =\frac{\mathrm{4}}{\mathrm{11}}×\frac{\mathrm{1}}{\mathrm{11}}=\frac{\mathrm{4}}{\mathrm{121}}\:\mathrm{watt} \\ $$
Commented by tawakalitu last updated on 16/Oct/16
Wow. God bless you sir.
$$\mathrm{Wow}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *