Question Number 8683 by 314159 last updated on 21/Oct/16

Commented by prakash jain last updated on 21/Oct/16
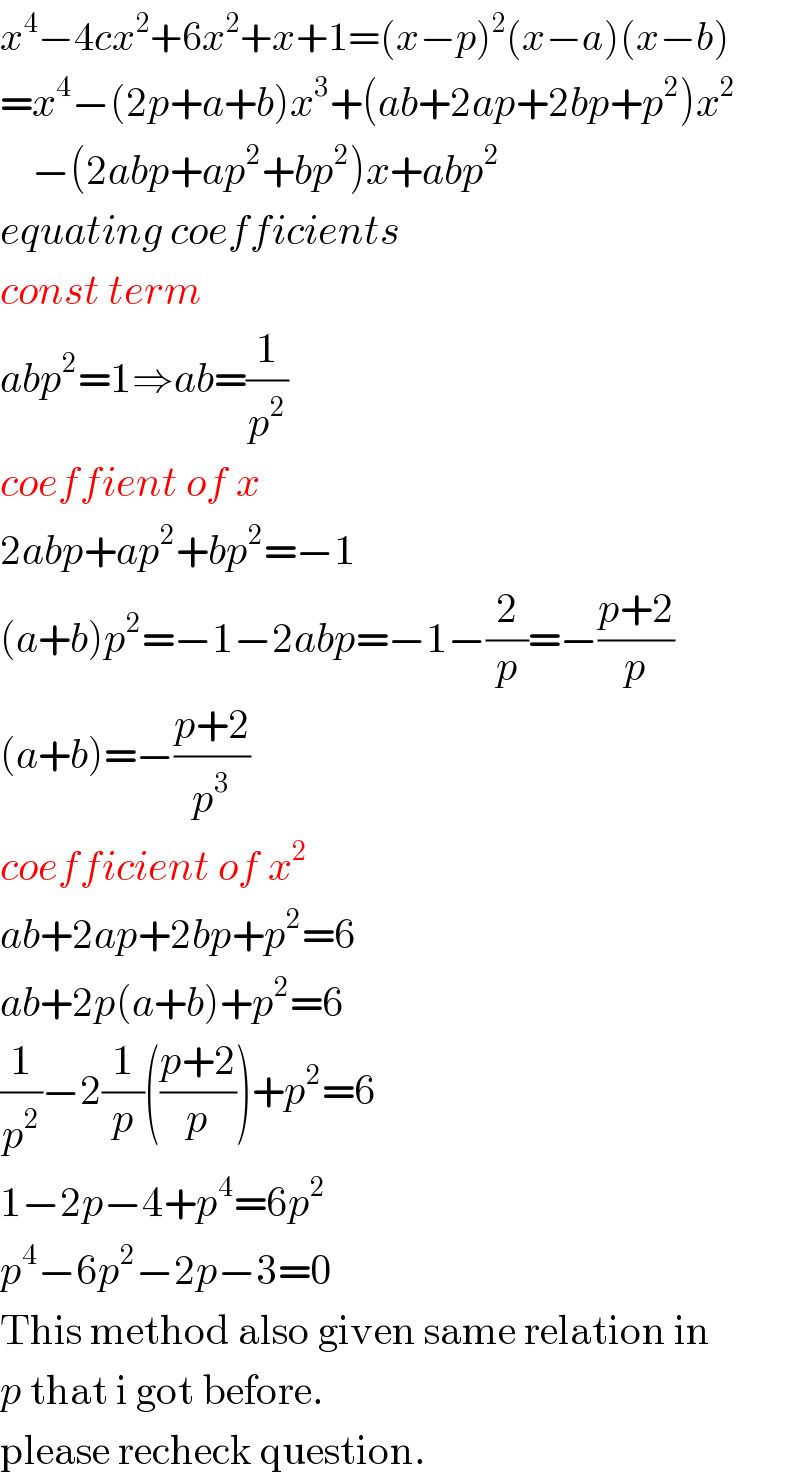
$${x}^{\mathrm{4}} −\mathrm{4}{cx}^{\mathrm{2}} +\mathrm{6}{x}^{\mathrm{2}} +{x}+\mathrm{1}=\left({x}−{p}\right)^{\mathrm{2}} \left({x}−{a}\right)\left({x}−{b}\right) \\ $$$$={x}^{\mathrm{4}} −\left(\mathrm{2}{p}+{a}+{b}\right){x}^{\mathrm{3}} +\left({ab}+\mathrm{2}{ap}+\mathrm{2}{bp}+{p}^{\mathrm{2}} \right){x}^{\mathrm{2}} \\ $$$$\:\:\:\:−\left(\mathrm{2}{abp}+{ap}^{\mathrm{2}} +{bp}^{\mathrm{2}} \right){x}+{abp}^{\mathrm{2}} \\ $$$${equating}\:{coefficients} \\ $$$${const}\:{term} \\ $$$${abp}^{\mathrm{2}} =\mathrm{1}\Rightarrow{ab}=\frac{\mathrm{1}}{{p}^{\mathrm{2}} } \\ $$$${coeffient}\:{of}\:{x} \\ $$$$\mathrm{2}{abp}+{ap}^{\mathrm{2}} +{bp}^{\mathrm{2}} =−\mathrm{1} \\ $$$$\left({a}+{b}\right){p}^{\mathrm{2}} =−\mathrm{1}−\mathrm{2}{abp}=−\mathrm{1}−\frac{\mathrm{2}}{{p}}=−\frac{{p}+\mathrm{2}}{{p}} \\ $$$$\left({a}+{b}\right)=−\frac{{p}+\mathrm{2}}{{p}^{\mathrm{3}} } \\ $$$${coefficient}\:{of}\:{x}^{\mathrm{2}} \\ $$$${ab}+\mathrm{2}{ap}+\mathrm{2}{bp}+{p}^{\mathrm{2}} =\mathrm{6} \\ $$$${ab}+\mathrm{2}{p}\left({a}+{b}\right)+{p}^{\mathrm{2}} =\mathrm{6} \\ $$$$\frac{\mathrm{1}}{{p}^{\mathrm{2}} }−\mathrm{2}\frac{\mathrm{1}}{{p}}\left(\frac{{p}+\mathrm{2}}{{p}}\right)+{p}^{\mathrm{2}} =\mathrm{6} \\ $$$$\mathrm{1}−\mathrm{2}{p}−\mathrm{4}+{p}^{\mathrm{4}} =\mathrm{6}{p}^{\mathrm{2}} \\ $$$${p}^{\mathrm{4}} −\mathrm{6}{p}^{\mathrm{2}} −\mathrm{2}{p}−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{This}\:\mathrm{method}\:\mathrm{also}\:\mathrm{given}\:\mathrm{same}\:\mathrm{relation}\:\mathrm{in} \\ $$$${p}\:\mathrm{that}\:\mathrm{i}\:\mathrm{got}\:\mathrm{before}. \\ $$$$\mathrm{please}\:\mathrm{recheck}\:\mathrm{question}. \\ $$
Commented by prakash jain last updated on 21/Oct/16
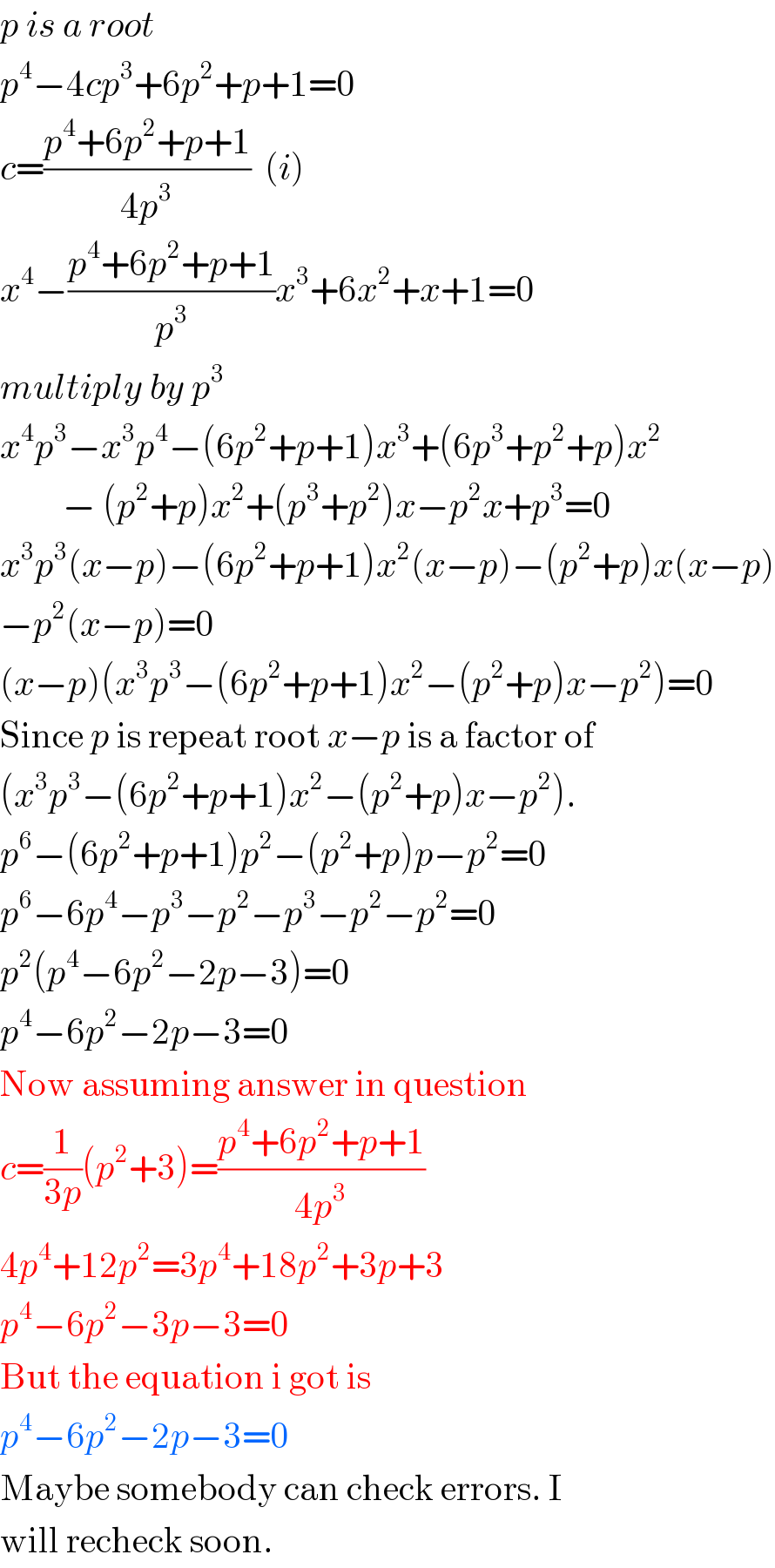
$${p}\:{is}\:{a}\:{root} \\ $$$${p}^{\mathrm{4}} −\mathrm{4}{cp}^{\mathrm{3}} +\mathrm{6}{p}^{\mathrm{2}} +{p}+\mathrm{1}=\mathrm{0} \\ $$$${c}=\frac{{p}^{\mathrm{4}} +\mathrm{6}{p}^{\mathrm{2}} +{p}+\mathrm{1}}{\mathrm{4}{p}^{\mathrm{3}} }\:\:\left({i}\right) \\ $$$${x}^{\mathrm{4}} −\frac{{p}^{\mathrm{4}} +\mathrm{6}{p}^{\mathrm{2}} +{p}+\mathrm{1}}{{p}^{\mathrm{3}} }{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0} \\ $$$${multiply}\:{by}\:{p}^{\mathrm{3}} \\ $$$${x}^{\mathrm{4}} {p}^{\mathrm{3}} −{x}^{\mathrm{3}} {p}^{\mathrm{4}} −\left(\mathrm{6}{p}^{\mathrm{2}} +{p}+\mathrm{1}\right){x}^{\mathrm{3}} +\left(\mathrm{6}{p}^{\mathrm{3}} +{p}^{\mathrm{2}} +{p}\right){x}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:−\:\left({p}^{\mathrm{2}} +{p}\right){x}^{\mathrm{2}} +\left({p}^{\mathrm{3}} +{p}^{\mathrm{2}} \right){x}−{p}^{\mathrm{2}} {x}+{p}^{\mathrm{3}} =\mathrm{0} \\ $$$${x}^{\mathrm{3}} {p}^{\mathrm{3}} \left({x}−{p}\right)−\left(\mathrm{6}{p}^{\mathrm{2}} +{p}+\mathrm{1}\right){x}^{\mathrm{2}} \left({x}−{p}\right)−\left({p}^{\mathrm{2}} +{p}\right){x}\left({x}−{p}\right) \\ $$$$−{p}^{\mathrm{2}} \left({x}−{p}\right)=\mathrm{0} \\ $$$$\left({x}−{p}\right)\left({x}^{\mathrm{3}} {p}^{\mathrm{3}} −\left(\mathrm{6}{p}^{\mathrm{2}} +{p}+\mathrm{1}\right){x}^{\mathrm{2}} −\left({p}^{\mathrm{2}} +{p}\right){x}−{p}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\mathrm{Since}\:{p}\:\mathrm{is}\:\mathrm{repeat}\:\mathrm{root}\:{x}−{p}\:\mathrm{is}\:\mathrm{a}\:\mathrm{factor}\:\mathrm{of} \\ $$$$\left({x}^{\mathrm{3}} {p}^{\mathrm{3}} −\left(\mathrm{6}{p}^{\mathrm{2}} +{p}+\mathrm{1}\right){x}^{\mathrm{2}} −\left({p}^{\mathrm{2}} +{p}\right){x}−{p}^{\mathrm{2}} \right). \\ $$$${p}^{\mathrm{6}} −\left(\mathrm{6}{p}^{\mathrm{2}} +{p}+\mathrm{1}\right){p}^{\mathrm{2}} −\left({p}^{\mathrm{2}} +{p}\right){p}−{p}^{\mathrm{2}} =\mathrm{0} \\ $$$${p}^{\mathrm{6}} −\mathrm{6}{p}^{\mathrm{4}} −{p}^{\mathrm{3}} −{p}^{\mathrm{2}} −{p}^{\mathrm{3}} −{p}^{\mathrm{2}} −{p}^{\mathrm{2}} =\mathrm{0} \\ $$$${p}^{\mathrm{2}} \left({p}^{\mathrm{4}} −\mathrm{6}{p}^{\mathrm{2}} −\mathrm{2}{p}−\mathrm{3}\right)=\mathrm{0} \\ $$$${p}^{\mathrm{4}} −\mathrm{6}{p}^{\mathrm{2}} −\mathrm{2}{p}−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{Now}\:\mathrm{assuming}\:\mathrm{answer}\:\mathrm{in}\:\mathrm{question} \\ $$$${c}=\frac{\mathrm{1}}{\mathrm{3}{p}}\left({p}^{\mathrm{2}} +\mathrm{3}\right)=\frac{{p}^{\mathrm{4}} +\mathrm{6}{p}^{\mathrm{2}} +{p}+\mathrm{1}}{\mathrm{4}{p}^{\mathrm{3}} } \\ $$$$\mathrm{4}{p}^{\mathrm{4}} +\mathrm{12}{p}^{\mathrm{2}} =\mathrm{3}{p}^{\mathrm{4}} +\mathrm{18}{p}^{\mathrm{2}} +\mathrm{3}{p}+\mathrm{3} \\ $$$${p}^{\mathrm{4}} −\mathrm{6}{p}^{\mathrm{2}} −\mathrm{3}{p}−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{But}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{i}\:\mathrm{got}\:\mathrm{is} \\ $$$${p}^{\mathrm{4}} −\mathrm{6}{p}^{\mathrm{2}} −\mathrm{2}{p}−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{Maybe}\:\mathrm{somebody}\:\mathrm{can}\:\mathrm{check}\:\mathrm{errors}.\:\mathrm{I} \\ $$$$\mathrm{will}\:\mathrm{recheck}\:\mathrm{soon}. \\ $$
Commented by prakash jain last updated on 23/Oct/16

$$\mathrm{314159},\:\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{not} \\ $$$$\mathrm{correct}\:\mathrm{did}\:\mathrm{u}\:\mathrm{try}\:\mathrm{to}\:\mathrm{go}\:\mathrm{thru}\:\mathrm{the}\:\mathrm{steps} \\ $$$$\mathrm{that}\:\mathrm{i}\:\mathrm{did}. \\ $$
