Question Number 8720 by www.matikzone.tk last updated on 24/Oct/16

Commented by prakash jain last updated on 24/Oct/16

$${what}\:{is}\:{meant}\:{by}\:{a}_{\mathrm{log}{c}} \\ $$
Commented by www.matikzone.tk last updated on 24/Oct/16

Commented by www.matikzone.tk last updated on 24/Oct/16
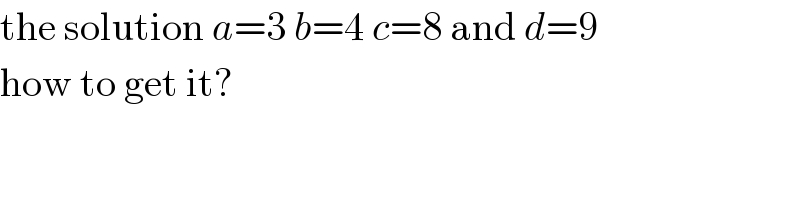
$$\mathrm{the}\:\mathrm{solution}\:{a}=\mathrm{3}\:{b}=\mathrm{4}\:{c}=\mathrm{8}\:\mathrm{and}\:{d}=\mathrm{9} \\ $$$$\mathrm{how}\:\mathrm{to}\:\mathrm{get}\:\mathrm{it}? \\ $$
Commented by prakash jain last updated on 24/Oct/16

$${d}=\mathrm{9},\:{a}=\mathrm{3} \\ $$$${d}−{a}=\mathrm{6} \\ $$$$\mathrm{Does}\:\mathrm{not}\:\mathrm{satisfy}\:{d}−{a}=\mathrm{7} \\ $$$$\mathrm{Should}\:\mathrm{be}\:{a}=\mathrm{2},{b}=\mathrm{4},{c}=\mathrm{8},\:{d}=\mathrm{9} \\ $$
Commented by prakash jain last updated on 24/Oct/16
![((ln 81)/(ln [((ln c)/(ln [((ln b)/(ln [((ln d)/(ln ((ln c)/(ln a))))]))]))]))=b ab=c d=a+7 This gives us 4 equations with three unknowns. a=2,b=4,c=8,d=9 ((ln 81)/(ln [((ln 8)/(ln [((ln 4)/(ln [((ln 9)/(ln ((ln 8)/(ln 2))))]))]))]))= ((ln 81)/(ln [((ln 8)/(ln [((ln 4)/(ln [((ln 9)/(ln 3))]))]))]))= ((ln 81)/(ln [((ln 8)/(ln [((ln 4)/(ln 2))]))]))=((ln 81)/(ln [((ln 8)/(ln 2))]))=((ln 81)/(ln 3))=4=b So this satisfies the equation. However given the fact there are only 3 equation with 4 unknown we can assume value for one of the variable and calculate theothers. So i start by assuming b=e then i calculated the following using wolfram alpha caculator. b=e=2.7182818284590.. a=1.7296241323821... c=4.70160606890820.. d=8.7296241323821... abcd=196.96921294... So there is no unique solution. The above solution also meets the condition.](https://www.tinkutara.com/question/Q8735.png)
$$\frac{\mathrm{ln}\:\mathrm{81}}{\mathrm{ln}\:\left[\frac{\mathrm{ln}\:{c}}{\mathrm{ln}\:\left[\frac{\mathrm{ln}\:{b}}{\mathrm{ln}\:\left[\frac{\mathrm{ln}\:{d}}{\mathrm{ln}\:\frac{\mathrm{ln}\:{c}}{\mathrm{ln}\:{a}}}\right]}\right]}\right]}={b} \\ $$$${ab}={c} \\ $$$${d}={a}+\mathrm{7} \\ $$$$\mathrm{This}\:\mathrm{gives}\:\mathrm{us}\:\mathrm{4}\:\mathrm{equations}\:\mathrm{with} \\ $$$$\mathrm{three}\:\mathrm{unknowns}. \\ $$$${a}=\mathrm{2},{b}=\mathrm{4},{c}=\mathrm{8},{d}=\mathrm{9} \\ $$$$\frac{\mathrm{ln}\:\mathrm{81}}{\mathrm{ln}\:\left[\frac{\mathrm{ln}\:\mathrm{8}}{\mathrm{ln}\:\left[\frac{\mathrm{ln}\:\mathrm{4}}{\mathrm{ln}\:\left[\frac{\mathrm{ln}\:\mathrm{9}}{\mathrm{ln}\:\frac{\mathrm{ln}\:\mathrm{8}}{\mathrm{ln}\:\mathrm{2}}}\right]}\right]}\right]}= \\ $$$$\frac{\mathrm{ln}\:\mathrm{81}}{\mathrm{ln}\:\left[\frac{\mathrm{ln}\:\mathrm{8}}{\mathrm{ln}\:\left[\frac{\mathrm{ln}\:\mathrm{4}}{\mathrm{ln}\:\left[\frac{\mathrm{ln}\:\mathrm{9}}{\mathrm{ln}\:\mathrm{3}}\right]}\right]}\right]}= \\ $$$$\frac{\mathrm{ln}\:\mathrm{81}}{\mathrm{ln}\:\left[\frac{\mathrm{ln}\:\mathrm{8}}{\mathrm{ln}\:\left[\frac{\mathrm{ln}\:\mathrm{4}}{\mathrm{ln}\:\mathrm{2}}\right]}\right]}=\frac{\mathrm{ln}\:\mathrm{81}}{\mathrm{ln}\:\left[\frac{\mathrm{ln}\:\mathrm{8}}{\mathrm{ln}\:\mathrm{2}}\right]}=\frac{\mathrm{ln}\:\mathrm{81}}{\mathrm{ln}\:\mathrm{3}}=\mathrm{4}={b} \\ $$$$\mathrm{So}\:\mathrm{this}\:\mathrm{satisfies}\:\mathrm{the}\:\mathrm{equation}. \\ $$$$\mathrm{However}\:\mathrm{given}\:\mathrm{the}\:\mathrm{fact}\:\mathrm{there}\:\mathrm{are} \\ $$$$\mathrm{only}\:\mathrm{3}\:\mathrm{equation}\:\mathrm{with}\:\mathrm{4}\:\mathrm{unknown} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{assume}\:\mathrm{value}\:\mathrm{for}\:\mathrm{one} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{variable}\:\mathrm{and}\:\mathrm{calculate}\:\mathrm{theothers}. \\ $$$$\mathrm{So}\:\mathrm{i}\:\mathrm{start}\:\mathrm{by}\:\mathrm{assuming}\:{b}={e} \\ $$$$\mathrm{then}\:\mathrm{i}\:\mathrm{calculated}\:\mathrm{the}\:\mathrm{following} \\ $$$$\mathrm{using}\:\mathrm{wolfram}\:\mathrm{alpha}\:\mathrm{caculator}. \\ $$$${b}={e}=\mathrm{2}.\mathrm{7182818284590}.. \\ $$$${a}=\mathrm{1}.\mathrm{7296241323821}… \\ $$$${c}=\mathrm{4}.\mathrm{70160606890820}.. \\ $$$${d}=\mathrm{8}.\mathrm{7296241323821}… \\ $$$${abcd}=\mathrm{196}.\mathrm{96921294}… \\ $$$$\mathrm{So}\:\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{unique}\:\mathrm{solution}. \\ $$$$\mathrm{The}\:\mathrm{above}\:\mathrm{solution}\:\mathrm{also}\:\mathrm{meets} \\ $$$$\mathrm{the}\:\mathrm{condition}. \\ $$
Answered by prakash jain last updated on 24/Oct/16

$$\mathrm{No}\:\mathrm{unique}\:\mathrm{solution}.\:\mathrm{See}\:\mathrm{explaination} \\ $$$$\mathrm{in}\:\mathrm{comments}. \\ $$
