Question Number 8785 by FilupSmith last updated on 27/Oct/16
Commented by FilupSmith last updated on 27/Oct/16
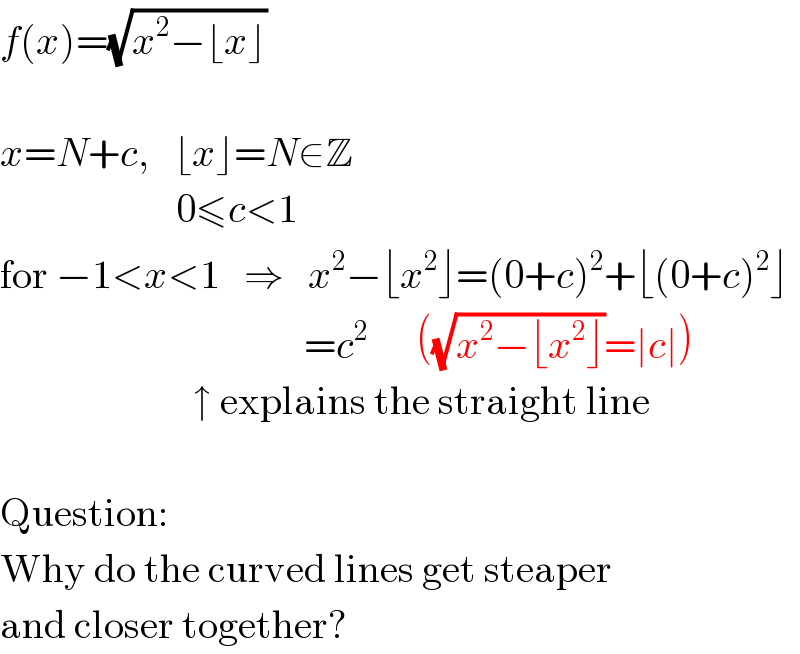
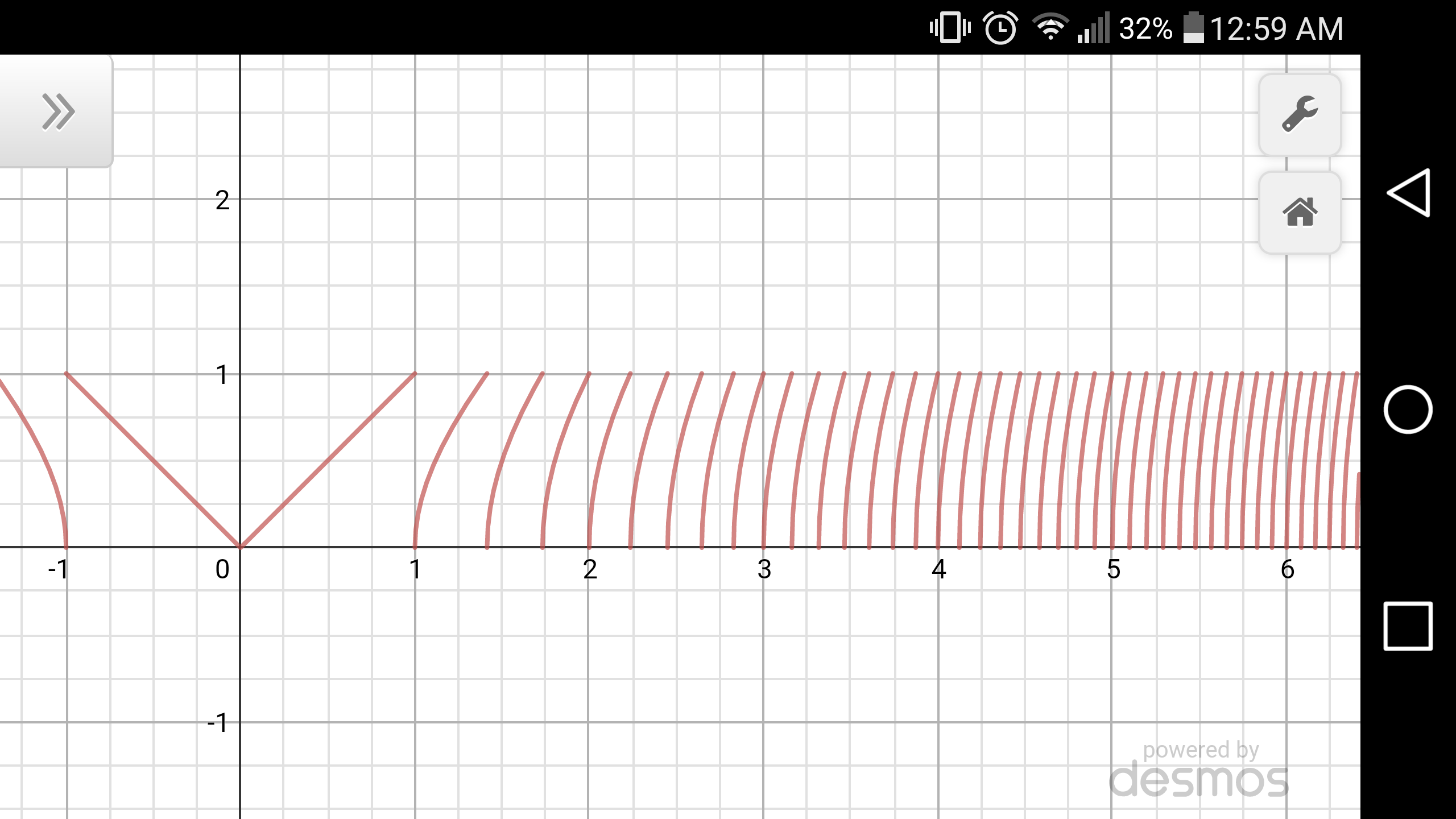
$${f}\left({x}\right)=\sqrt{{x}^{\mathrm{2}} −\lfloor{x}\rfloor} \\ $$$$\: \\ $$$${x}={N}+{c},\:\:\:\lfloor{x}\rfloor={N}\in\mathbb{Z} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\leqslant{c}<\mathrm{1} \\ $$$$\mathrm{for}\:−\mathrm{1}<{x}<\mathrm{1}\:\:\:\Rightarrow\:\:\:{x}^{\mathrm{2}} −\lfloor{x}^{\mathrm{2}} \rfloor=\left(\mathrm{0}+{c}\right)^{\mathrm{2}} +\lfloor\left(\mathrm{0}+{c}\right)^{\mathrm{2}} \rfloor \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={c}^{\mathrm{2}} \:\:\:\:\:\:\left(\sqrt{{x}^{\mathrm{2}} −\lfloor{x}^{\mathrm{2}} \rfloor}=\mid{c}\mid\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\uparrow\:\mathrm{explains}\:\mathrm{the}\:\mathrm{straight}\:\mathrm{line} \\ $$$$\: \\ $$$$\mathrm{Question}: \\ $$$$\mathrm{Why}\:\mathrm{do}\:\mathrm{the}\:\mathrm{curved}\:\mathrm{lines}\:\mathrm{get}\:\mathrm{steaper} \\ $$$$\mathrm{and}\:\mathrm{closer}\:\mathrm{together}? \\ $$
Commented by 123456 last updated on 27/Oct/16
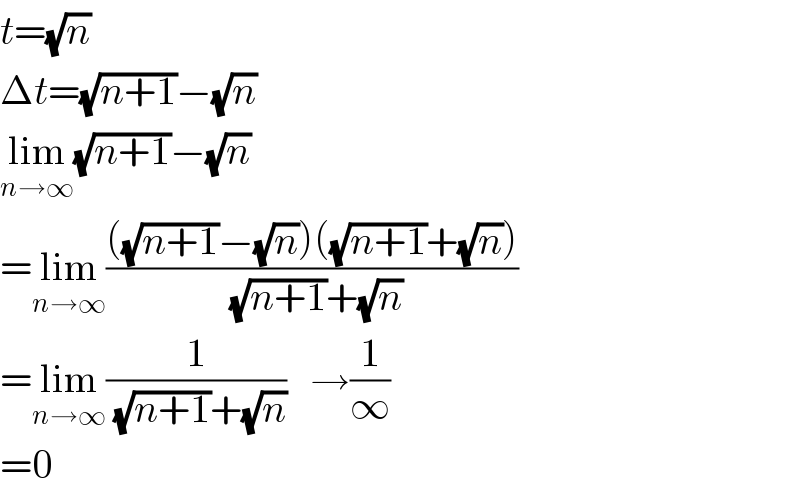
$${t}=\sqrt{{n}} \\ $$$$\Delta{t}=\sqrt{{n}+\mathrm{1}}−\sqrt{{n}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\sqrt{{n}+\mathrm{1}}−\sqrt{{n}} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\sqrt{{n}+\mathrm{1}}−\sqrt{{n}}\right)\left(\sqrt{{n}+\mathrm{1}}+\sqrt{{n}}\right)}{\:\sqrt{{n}+\mathrm{1}}+\sqrt{{n}}} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\:\sqrt{{n}+\mathrm{1}}+\sqrt{{n}}}\:\:\:\rightarrow\frac{\mathrm{1}}{\infty} \\ $$$$=\mathrm{0} \\ $$
Commented by FilupSmith last updated on 28/Oct/16
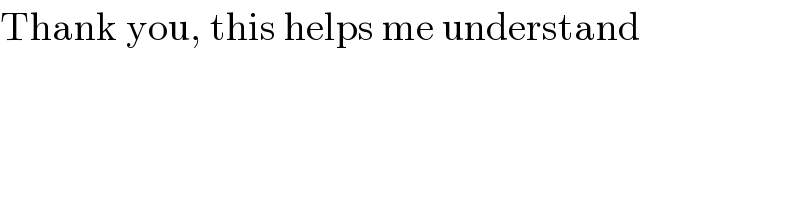
$$\mathrm{Thank}\:\mathrm{you},\:\mathrm{this}\:\mathrm{helps}\:\mathrm{me}\:\mathrm{understand} \\ $$
