Menu Close

Question-8847

Tinku Tara 0 Comments
Pin




Question Number 8847 by tawakalitu last updated on 31/Oct/16
Commented by Rasheed Soomro last updated on 01/Nov/16
Let r be the remainder in each case N is GCD of 1305−r,4665−r and 6905−r Let 1305−r=AN, 4665−r=BN and 6905−r=CN AN+r=1305 , BN+r=4665 and CN+r=6905 N(A+B+C)+3r=1305+4665+6905=12875 N=((12875−3r)/(A+B+C)) Continue
$$\mathrm{Let}\:\mathrm{r}\:\mathrm{be}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{in}\:\mathrm{each}\:\mathrm{case} \\ $$$$\mathrm{N}\:\mathrm{is}\:\mathrm{GCD}\:\mathrm{of}\:\mathrm{1305}−\mathrm{r},\mathrm{4665}−\mathrm{r}\:\mathrm{and}\:\mathrm{6905}−\mathrm{r} \\ $$$$\mathrm{Let}\:\mathrm{1305}−\mathrm{r}=\mathrm{AN},\:\mathrm{4665}−\mathrm{r}=\mathrm{BN}\:\:\mathrm{and}\:\:\mathrm{6905}−\mathrm{r}=\mathrm{CN} \\ $$$$\mathrm{AN}+\mathrm{r}=\mathrm{1305}\:,\:\mathrm{BN}+\mathrm{r}=\mathrm{4665}\:\:\mathrm{and}\:\:\mathrm{CN}+\mathrm{r}=\mathrm{6905} \\ $$$$\mathrm{N}\left(\mathrm{A}+\mathrm{B}+\mathrm{C}\right)+\mathrm{3r}=\mathrm{1305}+\mathrm{4665}+\mathrm{6905}=\mathrm{12875} \\ $$$$\mathrm{N}=\frac{\mathrm{12875}−\mathrm{3r}}{\mathrm{A}+\mathrm{B}+\mathrm{C}} \\ $$$$\mathrm{Continue} \\ $$
Commented by sandy_suhendra last updated on 01/Nov/16
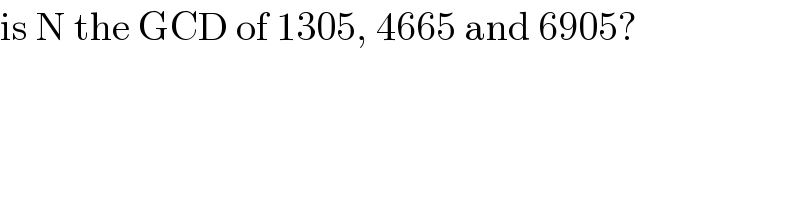
is N the GCD of 1305, 4665 and 6905?
$$\mathrm{is}\:\mathrm{N}\:\mathrm{the}\:\mathrm{GCD}\:\mathrm{of}\:\mathrm{1305},\:\mathrm{4665}\:\mathrm{and}\:\mathrm{6905}? \\ $$
Commented by sandy_suhendra last updated on 01/Nov/16
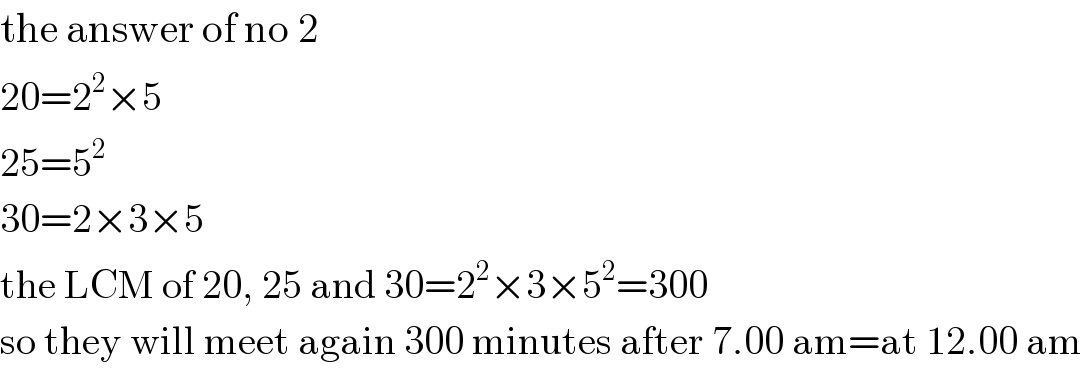
the answer of no 2 20=2^2 ×5 25=5^2 30=2×3×5 the LCM of 20, 25 and 30=2^2 ×3×5^2 =300 so they will meet again 300 minutes after 7.00 am=at 12.00 am
$$\mathrm{the}\:\mathrm{answer}\:\mathrm{of}\:\mathrm{no}\:\mathrm{2} \\ $$$$\mathrm{20}=\mathrm{2}^{\mathrm{2}} ×\mathrm{5} \\ $$$$\mathrm{25}=\mathrm{5}^{\mathrm{2}} \\ $$$$\mathrm{30}=\mathrm{2}×\mathrm{3}×\mathrm{5} \\ $$$$\mathrm{the}\:\mathrm{LCM}\:\mathrm{of}\:\mathrm{20},\:\mathrm{25}\:\mathrm{and}\:\mathrm{30}=\mathrm{2}^{\mathrm{2}} ×\mathrm{3}×\mathrm{5}^{\mathrm{2}} =\mathrm{300} \\ $$$$\mathrm{so}\:\mathrm{they}\:\mathrm{will}\:\mathrm{meet}\:\mathrm{again}\:\mathrm{300}\:\mathrm{minutes}\:\mathrm{after}\:\mathrm{7}.\mathrm{00}\:\mathrm{am}=\mathrm{at}\:\mathrm{12}.\mathrm{00}\:\mathrm{am} \\ $$
Commented by tawakalitu last updated on 01/Nov/16
i really appreciate sir=
$$\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}= \\ $$
Commented by tawakalitu last updated on 01/Nov/16
i really appreciate sir.
$$\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$
Answered by Rasheed Soomro last updated on 02/Nov/16
1. This depends upon remainder. If in general remainder is r. GCD of (1305−r) , (4665−r) and (6905−r) is G N=Max[G] determinant ((r,(1305−r),(4665−r),(6905−r),(GSD),(Sum)),(0,( 1305),( 4665),( 6905),( 5),( 5)),(1,( 1304),( 4664),( 6904),( 8),( 8)),(2,( 1303),( 4663),( 6903),1,( 1)),(3,( 1302),( 4662),( 6902),(14),( 5)),(4,( 1301),( 4661),( 6901),1,( 1)),(5,( 1300),( 4660),( 6900),(20),( 2)),(6,,,,,)) N=Max[ GSD′s of (1305−r) , (4665−r) and (6905−r) ] For a particular value/s of r , N is GSD of (1305−r) , (4665−r) and (6905−r). What is that r ? Continue
$$\mathrm{1}.\:\mathrm{This}\:\mathrm{depends}\:\mathrm{upon}\:\mathrm{remainder}. \\ $$$$\mathrm{If}\:\mathrm{in}\:\mathrm{general}\:\mathrm{remainder}\:\mathrm{is}\:\:\mathrm{r}. \\ $$$$\:\mathrm{GCD}\:\mathrm{of}\:\left(\mathrm{1305}−\mathrm{r}\right)\:,\:\left(\mathrm{4665}−\mathrm{r}\right)\:\:\mathrm{and}\:\:\left(\mathrm{6905}−\mathrm{r}\right)\:\mathrm{is}\:\mathrm{G} \\ $$$$\mathrm{N}=\mathrm{Max}\left[\mathrm{G}\right] \\ $$$$\begin{vmatrix}{\mathrm{r}}&{\mathrm{1305}−\mathrm{r}}&{\mathrm{4665}−\mathrm{r}}&{\mathrm{6905}−\mathrm{r}}&{\mathrm{GSD}}&{\mathrm{Sum}}\\{\mathrm{0}}&{\:\:\mathrm{1305}}&{\:\:\mathrm{4665}}&{\:\:\mathrm{6905}}&{\:\:\:\mathrm{5}}&{\:\:\:\mathrm{5}}\\{\mathrm{1}}&{\:\:\mathrm{1304}}&{\:\:\mathrm{4664}}&{\:\:\mathrm{6904}}&{\:\:\:\mathrm{8}}&{\:\:\:\mathrm{8}}\\{\mathrm{2}}&{\:\:\mathrm{1303}}&{\:\:\mathrm{4663}}&{\:\:\mathrm{6903}}&{\mathrm{1}}&{\:\:\mathrm{1}}\\{\mathrm{3}}&{\:\:\mathrm{1302}}&{\:\:\mathrm{4662}}&{\:\:\mathrm{6902}}&{\mathrm{14}}&{\:\:\mathrm{5}}\\{\mathrm{4}}&{\:\:\mathrm{1301}}&{\:\:\mathrm{4661}}&{\:\:\mathrm{6901}}&{\mathrm{1}}&{\:\:\mathrm{1}}\\{\mathrm{5}}&{\:\:\mathrm{1300}}&{\:\:\mathrm{4660}}&{\:\:\mathrm{6900}}&{\mathrm{20}}&{\:\:\mathrm{2}}\\{\mathrm{6}}&{}&{}&{}&{}&{}\end{vmatrix} \\ $$$$\mathrm{N}=\mathrm{Max}\left[\:\mathrm{GSD}'\mathrm{s}\:\mathrm{of}\:\left(\mathrm{1305}−\mathrm{r}\right)\:,\:\left(\mathrm{4665}−\mathrm{r}\right)\:\:\mathrm{and}\:\:\left(\mathrm{6905}−\mathrm{r}\right)\:\right] \\ $$$$\mathrm{For}\:\mathrm{a}\:\mathrm{particular}\:\mathrm{value}/\mathrm{s}\:\:\mathrm{of}\:\:\mathrm{r}\:,\:\mathrm{N}\:\mathrm{is}\:\mathrm{GSD}\:\mathrm{of} \\ $$$$\left(\mathrm{1305}−\mathrm{r}\right)\:,\:\left(\mathrm{4665}−\mathrm{r}\right)\:\:\mathrm{and}\:\:\left(\mathrm{6905}−\mathrm{r}\right). \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{that}\:\mathrm{r}\:? \\ $$$$\mathrm{Continue} \\ $$
Commented by tawakalitu last updated on 01/Nov/16
I really appreciate sir
$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir} \\ $$
Answered by Rasheed Soomro last updated on 03/Nov/16
N=Max [ GSD′s of (1305−r) , (4665−r) and (6905−r) ] where r is remainder left after division. See my other answer for detail. I think that the greatest GSD of (1305−r) , (4665−r) and (6905−r) occurs only when the GSD is 1305−r (minimum of three numbers) itself. So suppose 1305−r is GSD ((4665−r)/(1305−r)) is an integer 1,2,3,... Trying for these numbers we can see that 1,2,3 fail to achieve whole r >0 But 4 is successful: ((4665−r)/(1305−r))=4⇒r=185 Testing for all the three numbers 1305−r=1305−185=1120 (which is value of N) This number on dividing 1305,4665 and 6905 leaves the same remainder 185 and it is the greatest such number. So N=1120 and sum of digits is 1+1+2+0=4 Please confirm the answer if you know.
$$\mathrm{N}=\mathrm{Max}\:\left[\:\mathrm{GSD}'\mathrm{s}\:\mathrm{of}\:\left(\mathrm{1305}−\mathrm{r}\right)\:,\:\left(\mathrm{4665}−\mathrm{r}\right)\:\:\mathrm{and}\:\:\left(\mathrm{6905}−\mathrm{r}\right)\:\right] \\ $$$$\mathrm{where}\:\mathrm{r}\:\mathrm{is}\:\mathrm{remainder}\:\mathrm{left}\:\mathrm{after}\:\mathrm{division}.\:\mathrm{See}\:\mathrm{my}\:\mathrm{other}\: \\ $$$$\mathrm{answer}\:\mathrm{for}\:\mathrm{detail}. \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{that}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{GSD}\:\mathrm{of} \\ $$$$\left(\mathrm{1305}−\mathrm{r}\right)\:,\:\left(\mathrm{4665}−\mathrm{r}\right)\:\:\mathrm{and}\:\:\left(\mathrm{6905}−\mathrm{r}\right)\: \\ $$$$\mathrm{occurs}\:\:\:\mathrm{only}\:\mathrm{when}\:\mathrm{the}\:\mathrm{GSD}\:\mathrm{is}\:\mathrm{1305}−\mathrm{r}\:\left(\mathrm{minimum}\right. \\ $$$$\left.\mathrm{of}\:\mathrm{three}\:\mathrm{numbers}\right)\:\mathrm{itself}. \\ $$$$\mathrm{So}\:\mathrm{suppose}\:\mathrm{1305}−\mathrm{r}\:\:\mathrm{is}\:\:\mathrm{GSD} \\ $$$$\frac{\mathrm{4665}−\mathrm{r}}{\mathrm{1305}−\mathrm{r}}\:\mathrm{is}\:\mathrm{an}\:\mathrm{integer}\:\mathrm{1},\mathrm{2},\mathrm{3},… \\ $$$$\mathrm{Trying}\:\mathrm{for}\:\mathrm{these}\:\mathrm{numbers}\:\mathrm{we}\:\mathrm{can}\:\mathrm{see}\:\mathrm{that} \\ $$$$\mathrm{1},\mathrm{2},\mathrm{3}\:\mathrm{fail}\:\mathrm{to}\:\mathrm{achieve}\:\mathrm{whole}\:\mathrm{r}\:>\mathrm{0} \\ $$$$\mathrm{But}\:\mathrm{4}\:\mathrm{is}\:\mathrm{successful}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{4665}−\mathrm{r}}{\mathrm{1305}−\mathrm{r}}=\mathrm{4}\Rightarrow\mathrm{r}=\mathrm{185} \\ $$$$\mathrm{Testing}\:\mathrm{for}\:\mathrm{all}\:\mathrm{the}\:\mathrm{three}\:\mathrm{numbers} \\ $$$$\mathrm{1305}−\mathrm{r}=\mathrm{1305}−\mathrm{185}=\mathrm{1120}\:\left(\mathrm{which}\:\mathrm{is}\:\mathrm{value}\:\mathrm{of}\:\mathrm{N}\right) \\ $$$$\mathrm{This}\:\mathrm{number}\:\mathrm{on}\:\mathrm{dividing}\:\:\mathrm{1305},\mathrm{4665}\:\mathrm{and}\:\:\mathrm{6905} \\ $$$$\mathrm{leaves}\:\mathrm{the}\:\mathrm{same}\:\mathrm{remainder}\:\mathrm{185} \\ $$$$\mathrm{and}\:\mathrm{it}\:\mathrm{is}\:\mathrm{the}\:\:\mathrm{greatest}\:\mathrm{such}\:\mathrm{number}. \\ $$$$\mathrm{So}\:\mathrm{N}=\mathrm{1120}\:\mathrm{and}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{digits}\:\mathrm{is}\:\mathrm{1}+\mathrm{1}+\mathrm{2}+\mathrm{0}=\mathrm{4} \\ $$$$\mathrm{Please}\:\mathrm{confirm}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{if}\:\mathrm{you}\:\mathrm{know}. \\ $$$$ \\ $$
Commented by tawakalitu last updated on 03/Nov/16
Very correct sir. God bless you.
$$\mathrm{Very}\:\mathrm{correct}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *