Question Number 8860 by MNG last updated on 02/Nov/16
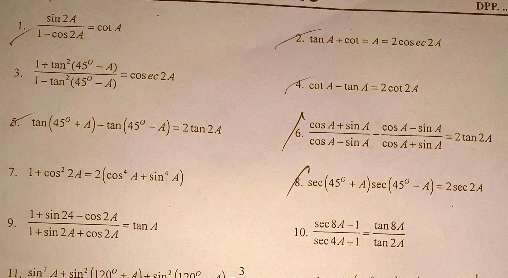
Commented by ridwan balatif last updated on 02/Nov/16

$$\mathrm{2}.\:\mathrm{tanA}+\mathrm{cotA}=\mathrm{2cosec2A} \\ $$$$\:\:\:\:\:\:\frac{\mathrm{sinA}}{\mathrm{cosA}}+\frac{\mathrm{cosA}}{\mathrm{sinA}}=\mathrm{2cosec2A} \\ $$$$\:\:\:\:\:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{A}+\mathrm{cos}^{\mathrm{2}} \mathrm{A}}{\mathrm{sinA}×\mathrm{cosA}}=\mathrm{2cosec2A} \\ $$$$\:\:\:\:\:\:\frac{\mathrm{1}}{\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin2A}\right)}=\mathrm{2cosec2A} \\ $$$$\:\:\:\:\:\:\:\mathrm{2cosec2A}\:=\mathrm{2cosec2A} \\ $$$$\mathrm{4}.\:\mathrm{cotA}−\mathrm{tanA}=\mathrm{2cot2A} \\ $$$$\:\:\:\:\:\:\frac{\mathrm{cosA}}{\mathrm{sinA}}−\frac{\mathrm{sinA}}{\mathrm{cosA}}=\mathrm{2cot2A} \\ $$$$\:\:\:\:\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{A}−\mathrm{sin}^{\mathrm{2}} \mathrm{A}}{\mathrm{sinA}×\mathrm{cosA}}=\mathrm{2cot2A} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{cos2A}}{\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin2A}\right)}=\mathrm{2cot2A} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2cot2A}\:=\mathrm{2cot2A} \\ $$
Answered by ridwan balatif last updated on 02/Nov/16

$$\mathrm{1}.\:\frac{\mathrm{sin2A}}{\mathrm{1}−\mathrm{cos2A}}=\mathrm{cotA}\: \\ $$$$\:\:\:\:\frac{\mathrm{sin2A}}{\mathrm{1}−\left(\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \mathrm{A}\right)}=\mathrm{cotA} \\ $$$$\:\:\:\:\frac{\mathrm{2sin}{A}\mathrm{cos}{A}}{\mathrm{2sin}^{\mathrm{2}} {A}}=\mathrm{cot}{A} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cot}{A}\:\:\:\:\:=\mathrm{cot}{A} \\ $$$$\mathrm{5}.\:\mathrm{tan}\left(\mathrm{45}^{\mathrm{o}} +\mathrm{A}\right)−\mathrm{tan}\left(\mathrm{45}^{\mathrm{o}} −\mathrm{A}\right)=\mathrm{2tan2A} \\ $$$$\:\:\:\:\:\frac{\mathrm{tan45}^{\mathrm{o}} +\mathrm{tanA}}{\mathrm{1}−\mathrm{tan45}^{\mathrm{o}} ×\mathrm{tanA}}−\left(\frac{\mathrm{tan45}^{\mathrm{o}} −\mathrm{tanA}}{\mathrm{1}+\mathrm{tan45}^{\mathrm{o}} ×\mathrm{tanA}}\right)=\mathrm{2tan2A} \\ $$$$\:\:\:\:\:\frac{\mathrm{1}+\mathrm{tanA}}{\mathrm{1}−\mathrm{tanA}}−\left(\frac{\mathrm{1}−\mathrm{tanA}}{\mathrm{1}+\mathrm{tanA}}\right)=\mathrm{2tan2A} \\ $$$$\:\:\:\:\:\:\frac{\left(\mathrm{1}+\mathrm{2tanA}+\mathrm{tan}^{\mathrm{2}} \mathrm{A}\right)−\left(\mathrm{1}−\mathrm{2tanA}+\mathrm{tan}^{\mathrm{2}} \mathrm{A}\right)}{\left(\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{A}\right)}=\mathrm{2tan2A} \\ $$$$\:\:\:\:\:\:\:\mathrm{2}×\left(\frac{\mathrm{tanA}+\mathrm{tanA}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \mathrm{A}}\right)=\mathrm{2tan2A} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2tan2A}\:\:\:\:\:\:=\mathrm{2tan2A} \\ $$
Answered by sandy_suhendra last updated on 03/Nov/16
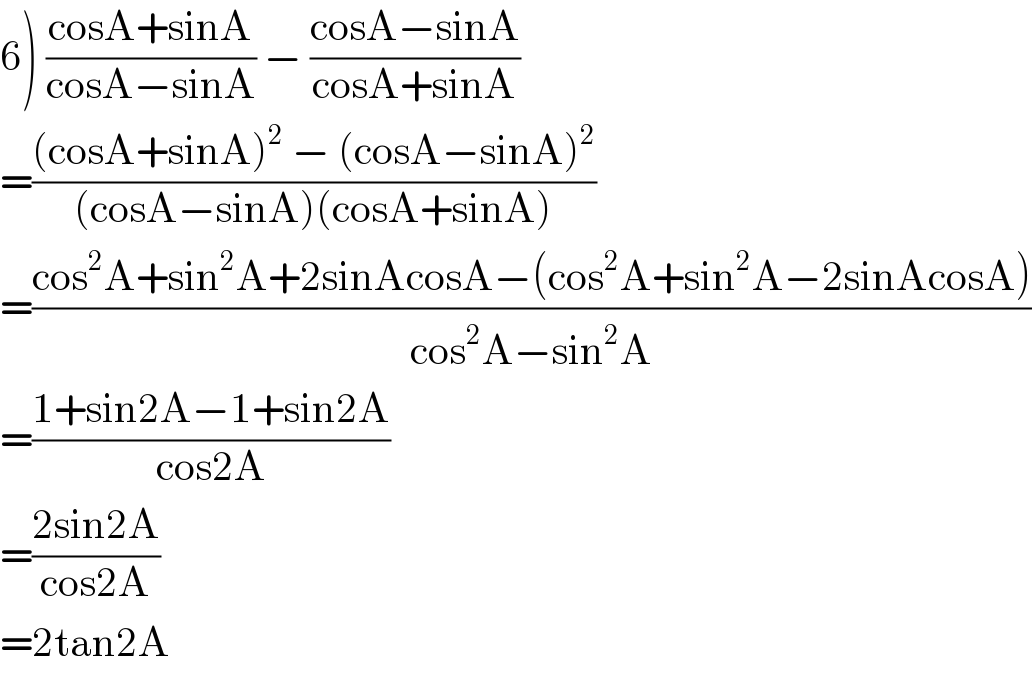
$$\left.\mathrm{6}\right)\:\frac{\mathrm{cosA}+\mathrm{sinA}}{\mathrm{cosA}−\mathrm{sinA}}\:−\:\frac{\mathrm{cosA}−\mathrm{sinA}}{\mathrm{cosA}+\mathrm{sinA}} \\ $$$$=\frac{\left(\mathrm{cosA}+\mathrm{sinA}\right)^{\mathrm{2}} \:−\:\left(\mathrm{cosA}−\mathrm{sinA}\right)^{\mathrm{2}} }{\left(\mathrm{cosA}−\mathrm{sinA}\right)\left(\mathrm{cosA}+\mathrm{sinA}\right)} \\ $$$$=\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{A}+\mathrm{sin}^{\mathrm{2}} \mathrm{A}+\mathrm{2sinAcosA}−\left(\mathrm{cos}^{\mathrm{2}} \mathrm{A}+\mathrm{sin}^{\mathrm{2}} \mathrm{A}−\mathrm{2sinAcosA}\right)}{\mathrm{cos}^{\mathrm{2}} \mathrm{A}−\mathrm{sin}^{\mathrm{2}} \mathrm{A}} \\ $$$$=\frac{\mathrm{1}+\mathrm{sin2A}−\mathrm{1}+\mathrm{sin2A}}{\mathrm{cos2A}} \\ $$$$=\frac{\mathrm{2sin2A}}{\mathrm{cos2A}} \\ $$$$=\mathrm{2tan2A} \\ $$
Answered by sandy_suhendra last updated on 03/Nov/16
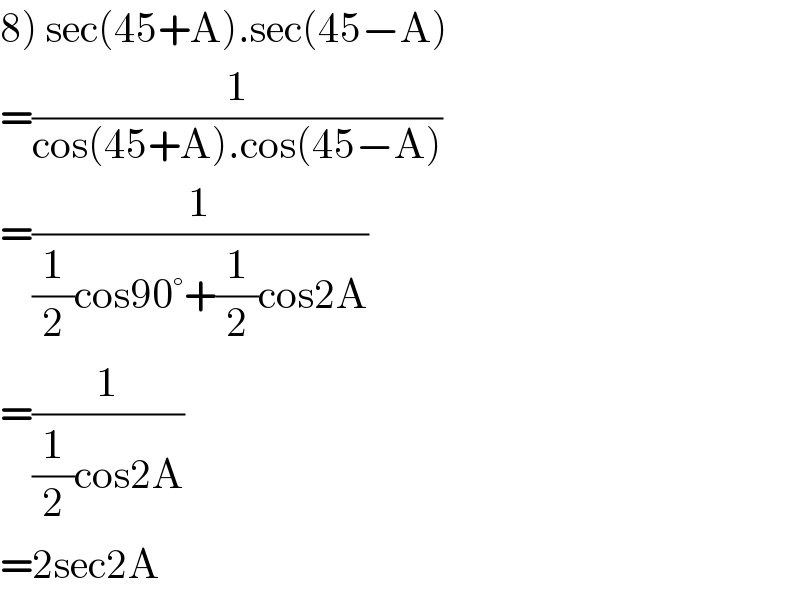
$$\left.\mathrm{8}\right)\:\mathrm{sec}\left(\mathrm{45}+\mathrm{A}\right).\mathrm{sec}\left(\mathrm{45}−\mathrm{A}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{cos}\left(\mathrm{45}+\mathrm{A}\right).\mathrm{cos}\left(\mathrm{45}−\mathrm{A}\right)} \\ $$$$=\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos90}°+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos2A}} \\ $$$$=\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos2A}} \\ $$$$=\mathrm{2sec2A} \\ $$
