Menu Close

Question-8877

Tinku Tara 0 Comments
Pin




Question Number 8877 by tawakalitu last updated on 03/Nov/16
Commented by Rasheed Soomro last updated on 03/Nov/16
Not related to this question. Please see my answers to your question #8847 and confirm whether the answer is correct or not.
$$\mathrm{Not}\:\mathrm{related}\:\mathrm{to}\:\mathrm{this}\:\mathrm{question}. \\ $$$$\mathrm{Please}\:\mathrm{see}\:\mathrm{my}\:\mathrm{answers}\:\mathrm{to}\:\mathrm{your} \\ $$$$\mathrm{question}\:#\mathrm{8847}\:\:\:\mathrm{and}\:\mathrm{confirm} \\ $$$$\mathrm{whether}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{correct} \\ $$$$\mathrm{or}\:\mathrm{not}. \\ $$
Commented by tawakalitu last updated on 03/Nov/16
i have confirm, it is correct sir. God bless you
$$\mathrm{i}\:\mathrm{have}\:\mathrm{confirm},\:\mathrm{it}\:\mathrm{is}\:\mathrm{correct}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\: \\ $$$$\mathrm{you} \\ $$
Commented by ridwan balatif last updated on 04/Nov/16
is it x is a decimal number or not?
$$\mathrm{is}\:\mathrm{it}\:\mathrm{x}\:\mathrm{is}\:\mathrm{a}\:\mathrm{decimal}\:\mathrm{number}\:\mathrm{or}\:\mathrm{not}? \\ $$
Answered by sandy_suhendra last updated on 03/Nov/16
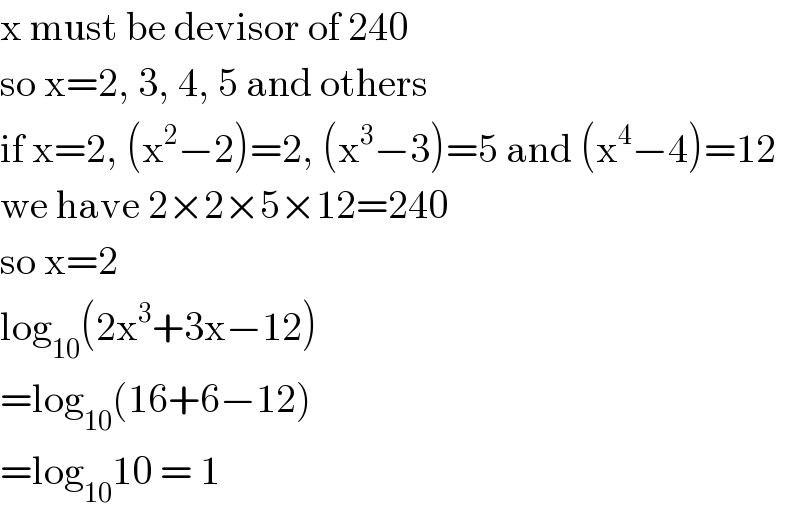
x must be devisor of 240 so x=2, 3, 4, 5 and others if x=2, (x^2 −2)=2, (x^3 −3)=5 and (x^4 −4)=12 we have 2×2×5×12=240 so x=2 log_(10) (2x^3 +3x−12) =log_(10) (16+6−12) =log_(10) 10 = 1
$$\mathrm{x}\:\mathrm{must}\:\mathrm{be}\:\mathrm{devisor}\:\mathrm{of}\:\mathrm{240} \\ $$$$\mathrm{so}\:\mathrm{x}=\mathrm{2},\:\mathrm{3},\:\mathrm{4},\:\mathrm{5}\:\mathrm{and}\:\mathrm{others} \\ $$$$\mathrm{if}\:\mathrm{x}=\mathrm{2},\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2}\right)=\mathrm{2},\:\left(\mathrm{x}^{\mathrm{3}} −\mathrm{3}\right)=\mathrm{5}\:\mathrm{and}\:\left(\mathrm{x}^{\mathrm{4}} −\mathrm{4}\right)=\mathrm{12} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{2}×\mathrm{2}×\mathrm{5}×\mathrm{12}=\mathrm{240} \\ $$$$\mathrm{so}\:\mathrm{x}=\mathrm{2} \\ $$$$\mathrm{log}_{\mathrm{10}} \left(\mathrm{2x}^{\mathrm{3}} +\mathrm{3x}−\mathrm{12}\right) \\ $$$$=\mathrm{log}_{\mathrm{10}} \left(\mathrm{16}+\mathrm{6}−\mathrm{12}\right) \\ $$$$=\mathrm{log}_{\mathrm{10}} \mathrm{10}\:=\:\mathrm{1} \\ $$
Commented by tawakalitu last updated on 03/Nov/16
Thanks so much sir. God bless you.
$$\mathrm{Thanks}\:\mathrm{so}\:\mathrm{much}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Answered by ridwan balatif last updated on 04/Nov/16
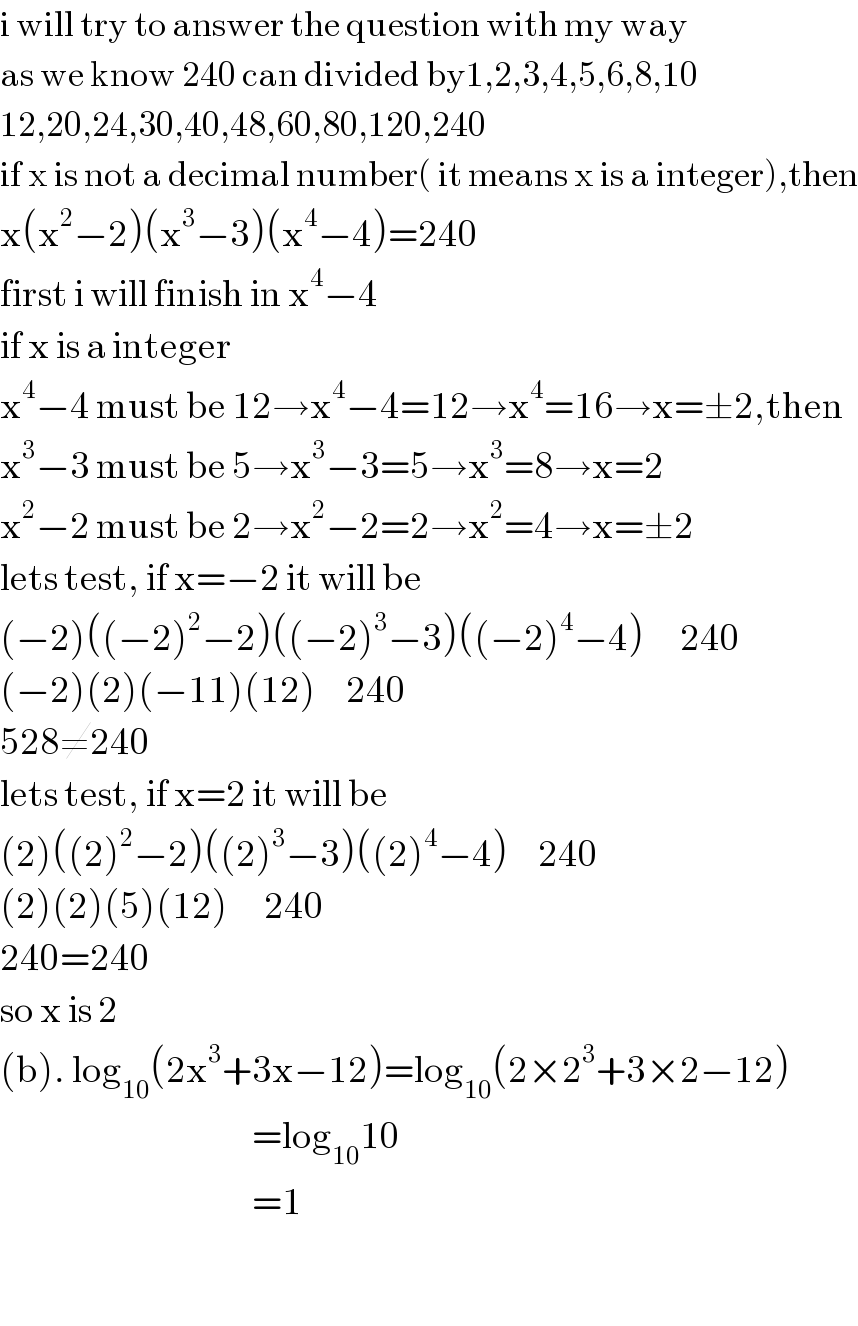
i will try to answer the question with my way as we know 240 can divided by1,2,3,4,5,6,8,10 12,20,24,30,40,48,60,80,120,240 if x is not a decimal number( it means x is a integer),then x(x^2 −2)(x^3 −3)(x^4 −4)=240 first i will finish in x^4 −4 if x is a integer x^4 −4 must be 12→x^4 −4=12→x^4 =16→x=±2,then x^3 −3 must be 5→x^3 −3=5→x^3 =8→x=2 x^2 −2 must be 2→x^2 −2=2→x^2 =4→x=±2 lets test, if x=−2 it will be (−2)((−2)^2 −2)((−2)^3 −3)((−2)^4 −4) 240 (−2)(2)(−11)(12) 240 528≠240 lets test, if x=2 it will be (2)((2)^2 −2)((2)^3 −3)((2)^4 −4) 240 (2)(2)(5)(12) 240 240=240 so x is 2 (b). log_(10) (2x^3 +3x−12)=log_(10) (2×2^3 +3×2−12) =log_(10) 10 =1
$$\mathrm{i}\:\mathrm{will}\:\mathrm{try}\:\mathrm{to}\:\mathrm{answer}\:\mathrm{the}\:\mathrm{question}\:\mathrm{with}\:\mathrm{my}\:\mathrm{way} \\ $$$$\mathrm{as}\:\mathrm{we}\:\mathrm{know}\:\mathrm{240}\:\mathrm{can}\:\mathrm{divided}\:\mathrm{by1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{6},\mathrm{8},\mathrm{10} \\ $$$$\mathrm{12},\mathrm{20},\mathrm{24},\mathrm{30},\mathrm{40},\mathrm{48},\mathrm{60},\mathrm{80},\mathrm{120},\mathrm{240} \\ $$$$\mathrm{if}\:\mathrm{x}\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:\mathrm{decimal}\:\mathrm{number}\left(\:\mathrm{it}\:\mathrm{means}\:\mathrm{x}\:\mathrm{is}\:\mathrm{a}\:\mathrm{integer}\right),\mathrm{then} \\ $$$$\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2}\right)\left(\mathrm{x}^{\mathrm{3}} −\mathrm{3}\right)\left(\mathrm{x}^{\mathrm{4}} −\mathrm{4}\right)=\mathrm{240} \\ $$$$\mathrm{first}\:\mathrm{i}\:\mathrm{will}\:\mathrm{finish}\:\mathrm{in}\:\mathrm{x}^{\mathrm{4}} −\mathrm{4} \\ $$$$\mathrm{if}\:\mathrm{x}\:\mathrm{is}\:\mathrm{a}\:\mathrm{integer} \\ $$$$\mathrm{x}^{\mathrm{4}} −\mathrm{4}\:\mathrm{must}\:\mathrm{be}\:\mathrm{12}\rightarrow\mathrm{x}^{\mathrm{4}} −\mathrm{4}=\mathrm{12}\rightarrow\mathrm{x}^{\mathrm{4}} =\mathrm{16}\rightarrow\mathrm{x}=\pm\mathrm{2},\mathrm{then} \\ $$$$\mathrm{x}^{\mathrm{3}} −\mathrm{3}\:\mathrm{must}\:\mathrm{be}\:\mathrm{5}\rightarrow\mathrm{x}^{\mathrm{3}} −\mathrm{3}=\mathrm{5}\rightarrow\mathrm{x}^{\mathrm{3}} =\mathrm{8}\rightarrow\mathrm{x}=\mathrm{2} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{2}\:\mathrm{must}\:\mathrm{be}\:\mathrm{2}\rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{2}=\mathrm{2}\rightarrow\mathrm{x}^{\mathrm{2}} =\mathrm{4}\rightarrow\mathrm{x}=\pm\mathrm{2} \\ $$$$\mathrm{lets}\:\mathrm{test},\:\mathrm{if}\:\mathrm{x}=−\mathrm{2}\:\mathrm{it}\:\mathrm{will}\:\mathrm{be} \\ $$$$\left(−\mathrm{2}\right)\left(\left(−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}\right)\left(\left(−\mathrm{2}\right)^{\mathrm{3}} −\mathrm{3}\right)\left(\left(−\mathrm{2}\right)^{\mathrm{4}} −\mathrm{4}\right)\:\:\:\:\:\:\mathrm{240} \\ $$$$\left(−\mathrm{2}\right)\left(\mathrm{2}\right)\left(−\mathrm{11}\right)\left(\mathrm{12}\right)\:\:\:\:\:\mathrm{240} \\ $$$$\mathrm{528}\neq\mathrm{240} \\ $$$$\mathrm{lets}\:\mathrm{test},\:\mathrm{if}\:\mathrm{x}=\mathrm{2}\:\mathrm{it}\:\mathrm{will}\:\mathrm{be} \\ $$$$\left(\mathrm{2}\right)\left(\left(\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}\right)\left(\left(\mathrm{2}\right)^{\mathrm{3}} −\mathrm{3}\right)\left(\left(\mathrm{2}\right)^{\mathrm{4}} −\mathrm{4}\right)\:\:\:\:\:\mathrm{240} \\ $$$$\left(\mathrm{2}\right)\left(\mathrm{2}\right)\left(\mathrm{5}\right)\left(\mathrm{12}\right)\:\:\:\:\:\:\mathrm{240} \\ $$$$\mathrm{240}=\mathrm{240} \\ $$$$\mathrm{so}\:\mathrm{x}\:\mathrm{is}\:\mathrm{2} \\ $$$$\left(\mathrm{b}\right).\:\mathrm{log}_{\mathrm{10}} \left(\mathrm{2x}^{\mathrm{3}} +\mathrm{3x}−\mathrm{12}\right)=\mathrm{log}_{\mathrm{10}} \left(\mathrm{2}×\mathrm{2}^{\mathrm{3}} +\mathrm{3}×\mathrm{2}−\mathrm{12}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{log}_{\mathrm{10}} \mathrm{10} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1} \\ $$$$ \\ $$
Commented by tawakalitu last updated on 04/Nov/16
i really appreciate sir. God bless you.
$$\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *