Question Number 8888 by 7C;00 last updated on 04/Nov/16
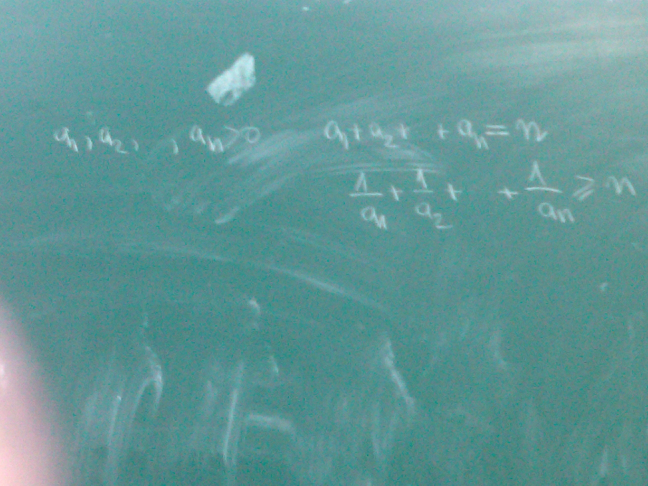
Commented by prakash jain last updated on 04/Nov/16

$$\mathrm{for}\:\mathrm{positive}\:\mathrm{numbers}: \\ $$$$\mathrm{Arithmetic}\:\mathrm{mean}\:\geqslant\:\mathrm{Harmonic}\:\mathrm{mean} \\ $$$$\mathrm{AM}=\frac{{a}_{\mathrm{1}} +{a}_{\mathrm{2}} +…+{a}_{{n}} }{{n}}=\frac{{n}}{{n}}=\mathrm{1} \\ $$$$\mathrm{HM}=\frac{{n}}{\frac{\mathrm{1}}{{a}_{\mathrm{1}} }+\frac{\mathrm{1}}{{a}_{\mathrm{2}} }+\frac{\mathrm{1}}{{a}_{\mathrm{3}} }+…+\frac{\mathrm{1}}{{a}_{{n}} }} \\ $$$$\mathrm{1}\geqslant\frac{{n}}{\frac{\mathrm{1}}{{a}_{\mathrm{1}} }+\frac{\mathrm{1}}{{a}_{\mathrm{2}} }+\frac{\mathrm{1}}{{a}_{\mathrm{3}} }+…+\frac{\mathrm{1}}{{a}_{{n}} }} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{a}_{\mathrm{1}} }+\frac{\mathrm{1}}{{a}_{\mathrm{2}} }+\frac{\mathrm{1}}{{a}_{\mathrm{3}} }+…+\frac{\mathrm{1}}{{a}_{{n}} }\geqslant{n} \\ $$
Answered by Chantria last updated on 08/Nov/16

$$\boldsymbol{\mathrm{Solution}}. \\ $$$$\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{a}}_{\mathrm{1}} ,\boldsymbol{\mathrm{a}}_{\mathrm{2}} ,…,\boldsymbol{\mathrm{a}}_{\boldsymbol{\mathrm{n}}} >\mathrm{0}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{b}}_{\mathrm{1}} ,\boldsymbol{\mathrm{b}}_{\mathrm{2}} ,…,\boldsymbol{\mathrm{b}}_{\boldsymbol{\mathrm{n}}} >\mathrm{0} \\ $$$$\boldsymbol{\mathrm{by}}\:\boldsymbol{\mathrm{Cauchy}}−\boldsymbol{\mathrm{Schwarz}}\:\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{eagle}}\:\boldsymbol{\mathrm{form}} \\ $$$$\:\frac{\boldsymbol{\mathrm{a}}_{\mathrm{1}} ^{\mathrm{2}} }{\boldsymbol{\mathrm{b}}_{\mathrm{1}} }+\frac{\boldsymbol{\mathrm{a}}_{\mathrm{2}} ^{\mathrm{2}} }{\boldsymbol{\mathrm{b}}_{\mathrm{2}} }+…+\frac{\boldsymbol{\mathrm{a}}_{\boldsymbol{\mathrm{n}}} ^{\mathrm{2}} }{\boldsymbol{\mathrm{b}}_{\boldsymbol{\mathrm{n}}} }\geqslant\frac{\left(\boldsymbol{\mathrm{a}}_{\mathrm{1}} +\boldsymbol{\mathrm{a}}_{\mathrm{2}} +…+\boldsymbol{\mathrm{a}}_{\boldsymbol{\mathrm{n}}} \right)^{\mathrm{2}} }{\boldsymbol{\mathrm{b}}_{\mathrm{1}} +\boldsymbol{\mathrm{b}}_{\mathrm{2}} +…+\boldsymbol{\mathrm{b}}_{\boldsymbol{\mathrm{n}}} } \\ $$$$\frac{\mathrm{1}^{\mathrm{2}} }{\boldsymbol{\mathrm{a}}_{\mathrm{1}} }+\frac{\mathrm{1}^{\mathrm{2}} }{\boldsymbol{\mathrm{a}}_{\mathrm{2}} }+…+\frac{\mathrm{1}^{\mathrm{2}} }{\boldsymbol{\mathrm{a}}_{\boldsymbol{\mathrm{n}}} }\geqslant\frac{\left(\mathrm{1}+\mathrm{1}+…+\mathrm{1}\right)^{\mathrm{2}} }{\boldsymbol{\mathrm{a}}_{\mathrm{1}} +\boldsymbol{\mathrm{a}}_{\mathrm{2}} +…+\boldsymbol{\mathrm{a}}_{\boldsymbol{\mathrm{n}}} }=\frac{\boldsymbol{\mathrm{n}}^{\mathrm{2}} }{\boldsymbol{\mathrm{n}}}=\boldsymbol{\mathrm{n}} \\ $$$$\:\boldsymbol{\mathrm{because}}\:\boldsymbol{\mathrm{a}}_{\mathrm{1}} +\boldsymbol{\mathrm{a}}_{\mathrm{2}} +…+\boldsymbol{\mathrm{a}}_{\boldsymbol{\mathrm{n}}} =\boldsymbol{\mathrm{n}} \\ $$
