Question-9048

Question Number 9048 by tawakalitu last updated on 16/Nov/16

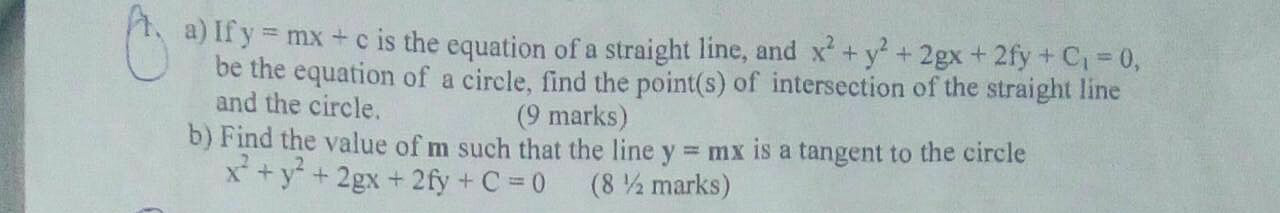
Answered by Rasheed Soomro last updated on 16/Nov/16

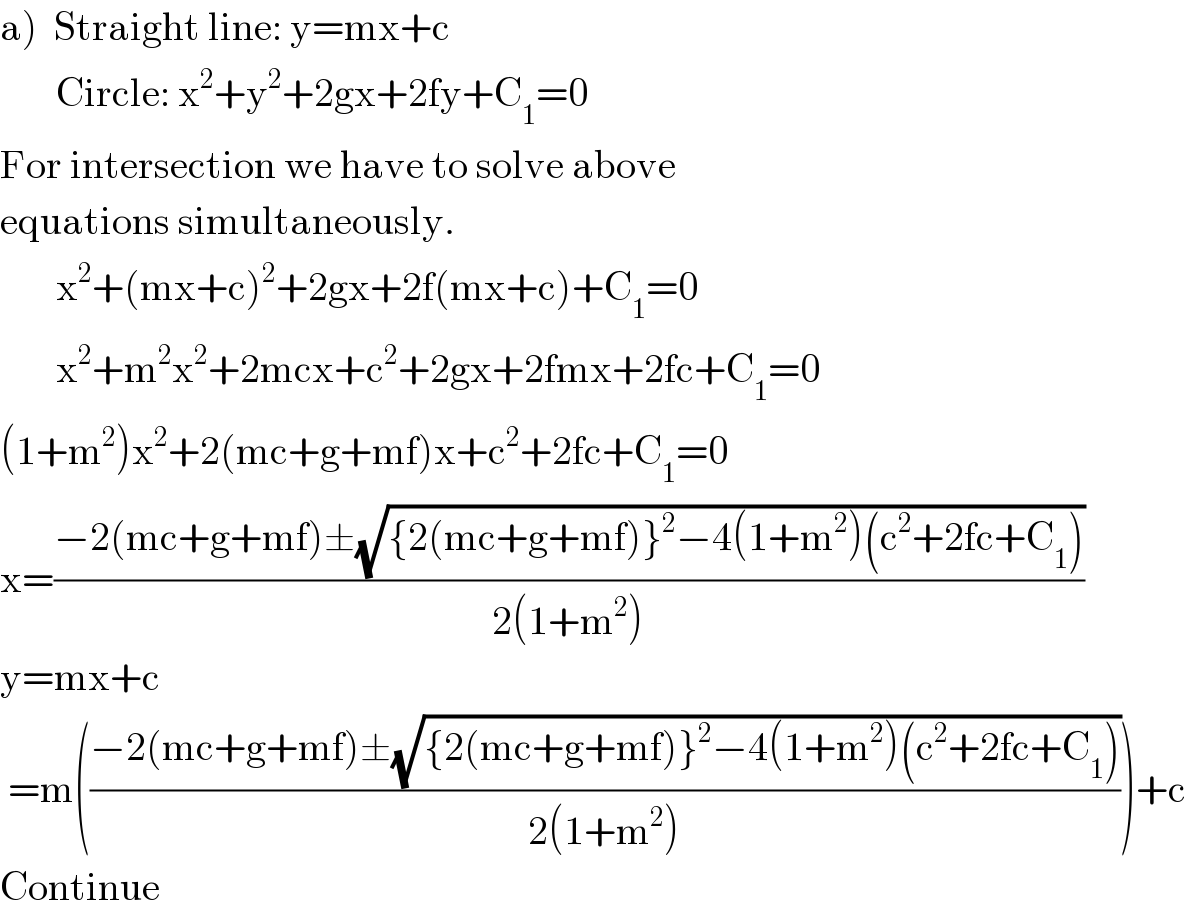
a) Straight line: y=mx+c Circle: x^2 +y^2 +2gx+2fy+C_1 =0 For intersection we have to solve above equations simultaneously. x^2 +(mx+c)^2 +2gx+2f(mx+c)+C_1 =0 x^2 +m^2 x^2 +2mcx+c^2 +2gx+2fmx+2fc+C_1 =0 (1+m^2 )x^2 +2(mc+g+mf)x+c^2 +2fc+C_1 =0 x=((−2(mc+g+mf)±(√({2(mc+g+mf)}^2 −4(1+m^2 )(c^2 +2fc+C_1 ))))/(2(1+m^2 ))) y=mx+c =m(((−2(mc+g+mf)±(√({2(mc+g+mf)}^2 −4(1+m^2 )(c^2 +2fc+C_1 ))))/(2(1+m^2 ))))+c Continue

$$\left.\mathrm{a}\right)\:\:\mathrm{Straight}\:\mathrm{line}:\:\mathrm{y}=\mathrm{mx}+\mathrm{c} \\ $$$$\:\:\:\:\:\:\:\mathrm{Circle}:\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{2gx}+\mathrm{2fy}+\mathrm{C}_{\mathrm{1}} =\mathrm{0} \\ $$$$\mathrm{For}\:\mathrm{intersection}\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{above} \\ $$$$\mathrm{equations}\:\mathrm{simultaneously}. \\ $$$$\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} +\left(\mathrm{mx}+\mathrm{c}\right)^{\mathrm{2}} +\mathrm{2gx}+\mathrm{2f}\left(\mathrm{mx}+\mathrm{c}\right)+\mathrm{C}_{\mathrm{1}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} +\mathrm{m}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} +\mathrm{2mcx}+\mathrm{c}^{\mathrm{2}} +\mathrm{2gx}+\mathrm{2fmx}+\mathrm{2fc}+\mathrm{C}_{\mathrm{1}} =\mathrm{0} \\ $$$$\left(\mathrm{1}+\mathrm{m}^{\mathrm{2}} \right)\mathrm{x}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{mc}+\mathrm{g}+\mathrm{mf}\right)\mathrm{x}+\mathrm{c}^{\mathrm{2}} +\mathrm{2fc}+\mathrm{C}_{\mathrm{1}} =\mathrm{0} \\ $$$$\mathrm{x}=\frac{−\mathrm{2}\left(\mathrm{mc}+\mathrm{g}+\mathrm{mf}\right)\pm\sqrt{\left\{\mathrm{2}\left(\mathrm{mc}+\mathrm{g}+\mathrm{mf}\right)\right\}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}+\mathrm{m}^{\mathrm{2}} \right)\left(\mathrm{c}^{\mathrm{2}} +\mathrm{2fc}+\mathrm{C}_{\mathrm{1}} \right)}}{\mathrm{2}\left(\mathrm{1}+\mathrm{m}^{\mathrm{2}} \right)} \\ $$$$\mathrm{y}=\mathrm{mx}+\mathrm{c} \\ $$$$\:=\mathrm{m}\left(\frac{−\mathrm{2}\left(\mathrm{mc}+\mathrm{g}+\mathrm{mf}\right)\pm\sqrt{\left\{\mathrm{2}\left(\mathrm{mc}+\mathrm{g}+\mathrm{mf}\right)\right\}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}+\mathrm{m}^{\mathrm{2}} \right)\left(\mathrm{c}^{\mathrm{2}} +\mathrm{2fc}+\mathrm{C}_{\mathrm{1}} \right)}}{\mathrm{2}\left(\mathrm{1}+\mathrm{m}^{\mathrm{2}} \right)}\right)+\mathrm{c} \\ $$$$\mathrm{Continue} \\ $$

Commented by tawakalitu last updated on 16/Nov/16

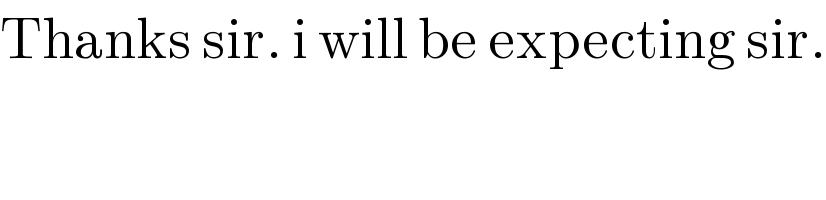
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{will}\:\mathrm{be}\:\mathrm{expecting}\:\mathrm{sir}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply