Menu Close

Question-9069

Tinku Tara 0 Comments
Pin




Question Number 9069 by tawakalitu last updated on 16/Nov/16
Commented by RasheedSoomro last updated on 20/Nov/16
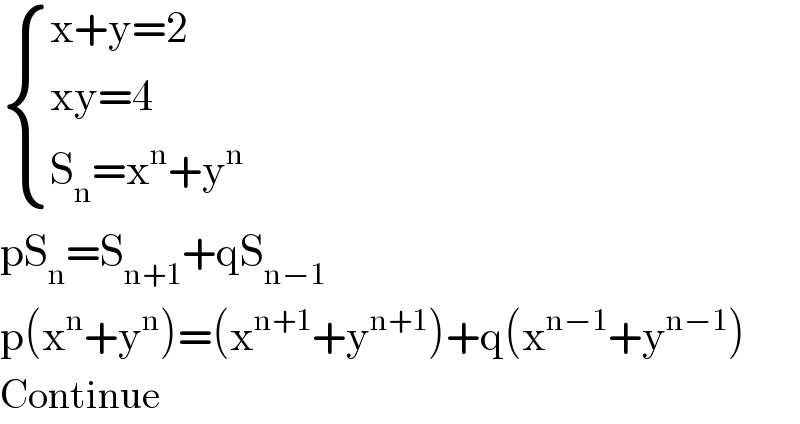
{ ((x+y=2)),((xy=4)),((S_n =x^n +y^n )) :} pS_n =S_(n+1) +qS_(n−1) p(x^n +y^n )=(x^(n+1) +y^(n+1) )+q(x^(n−1) +y^(n−1) ) Continue
{x+y=2xy=4Sn=xn+ynpSn=Sn+1+qSn−1p(xn+yn)=(xn+1+yn+1)+q(xn−1+yn−1)Continue
Commented by tawakalitu last updated on 20/Nov/16
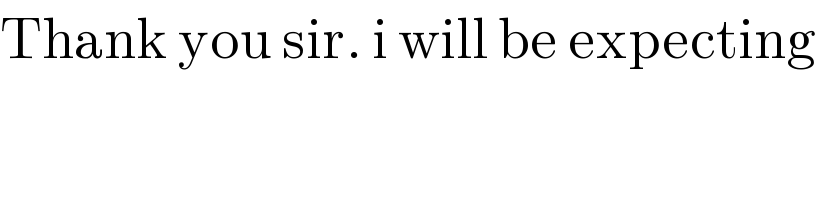
Thank you sir. i will be expecting
Thankyousir.iwillbeexpecting

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *