Menu Close

Question-9254

Tinku Tara 0 Comments
Pin




Question Number 9254 by tawakalitu last updated on 25/Nov/16
Answered by mrW last updated on 26/Nov/16
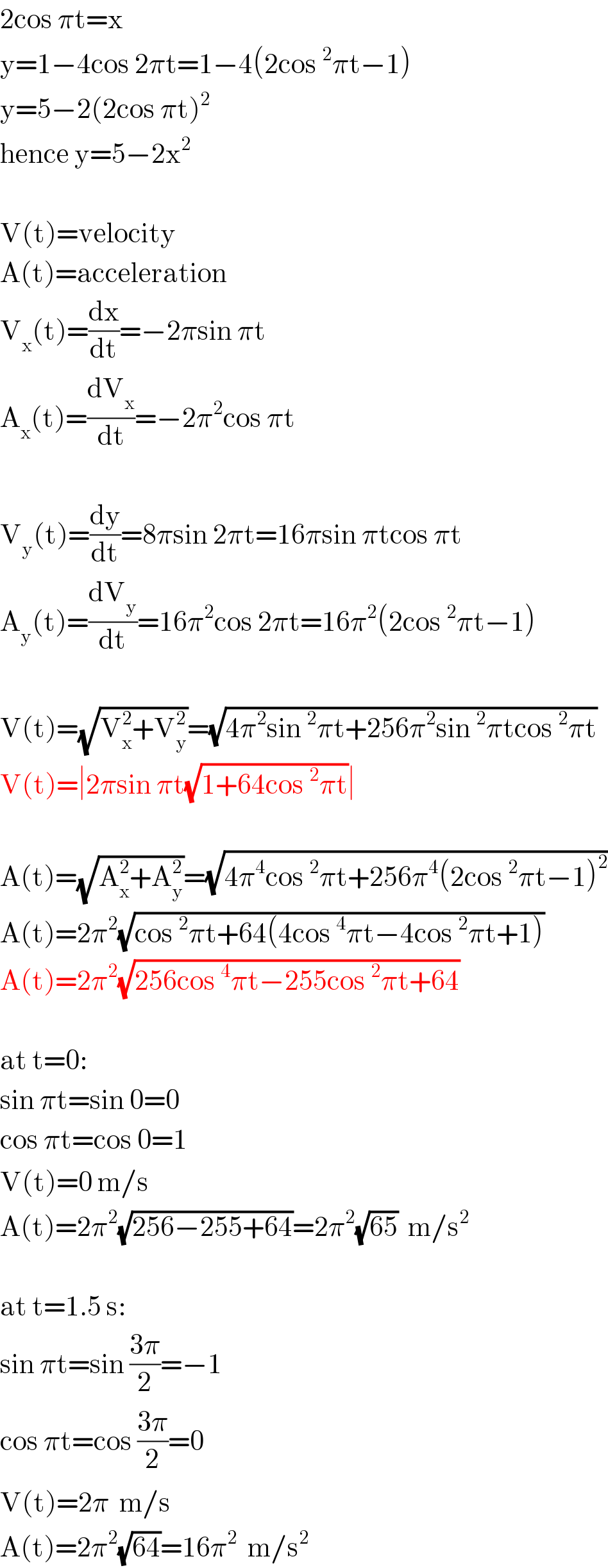
2cos πt=x y=1−4cos 2πt=1−4(2cos^2 πt−1) y=5−2(2cos πt)^2 hence y=5−2x^2 V(t)=velocity A(t)=acceleration V_x (t)=(dx/dt)=−2πsin πt A_x (t)=(dV_x /dt)=−2π^2 cos πt V_y (t)=(dy/dt)=8πsin 2πt=16πsin πtcos πt A_y (t)=(dV_y /dt)=16π^2 cos 2πt=16π^2 (2cos^2 πt−1) V(t)=(√(V_x ^2 +V_y ^2 ))=(√(4π^2 sin^2 πt+256π^2 sin^2 πtcos^2 πt)) V(t)=∣2πsin πt(√(1+64cos^2 πt))∣ A(t)=(√(A_x ^2 +A_y ^2 ))=(√(4π^4 cos^2 πt+256π^4 (2cos^2 πt−1)^2 )) A(t)=2π^2 (√(cos^2 πt+64(4cos^4 πt−4cos^2 πt+1))) A(t)=2π^2 (√(256cos^4 πt−255cos^2 πt+64)) at t=0: sin πt=sin 0=0 cos πt=cos 0=1 V(t)=0 m/s A(t)=2π^2 (√(256−255+64))=2π^2 (√(65)) m/s^2 at t=1.5 s: sin πt=sin ((3π)/2)=−1 cos πt=cos ((3π)/2)=0 V(t)=2π m/s A(t)=2π^2 (√(64))=16π^2 m/s^2
$$\mathrm{2cos}\:\pi\mathrm{t}=\mathrm{x} \\ $$$$\mathrm{y}=\mathrm{1}−\mathrm{4cos}\:\mathrm{2}\pi\mathrm{t}=\mathrm{1}−\mathrm{4}\left(\mathrm{2cos}\:^{\mathrm{2}} \pi\mathrm{t}−\mathrm{1}\right) \\ $$$$\mathrm{y}=\mathrm{5}−\mathrm{2}\left(\mathrm{2cos}\:\pi\mathrm{t}\right)^{\mathrm{2}} \\ $$$$\mathrm{hence}\:\mathrm{y}=\mathrm{5}−\mathrm{2x}^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{V}\left(\mathrm{t}\right)=\mathrm{velocity} \\ $$$$\mathrm{A}\left(\mathrm{t}\right)=\mathrm{acceleration} \\ $$$$\mathrm{V}_{\mathrm{x}} \left(\mathrm{t}\right)=\frac{\mathrm{dx}}{\mathrm{dt}}=−\mathrm{2}\pi\mathrm{sin}\:\pi\mathrm{t} \\ $$$$\mathrm{A}_{\mathrm{x}} \left(\mathrm{t}\right)=\frac{\mathrm{dV}_{\mathrm{x}} }{\mathrm{dt}}=−\mathrm{2}\pi^{\mathrm{2}} \mathrm{cos}\:\pi\mathrm{t} \\ $$$$ \\ $$$$\mathrm{V}_{\mathrm{y}} \left(\mathrm{t}\right)=\frac{\mathrm{dy}}{\mathrm{dt}}=\mathrm{8}\pi\mathrm{sin}\:\mathrm{2}\pi\mathrm{t}=\mathrm{16}\pi\mathrm{sin}\:\pi\mathrm{tcos}\:\pi\mathrm{t} \\ $$$$\mathrm{A}_{\mathrm{y}} \left(\mathrm{t}\right)=\frac{\mathrm{dV}_{\mathrm{y}} }{\mathrm{dt}}=\mathrm{16}\pi^{\mathrm{2}} \mathrm{cos}\:\mathrm{2}\pi\mathrm{t}=\mathrm{16}\pi^{\mathrm{2}} \left(\mathrm{2cos}\:^{\mathrm{2}} \pi\mathrm{t}−\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{V}\left(\mathrm{t}\right)=\sqrt{\mathrm{V}_{\mathrm{x}} ^{\mathrm{2}} +\mathrm{V}_{\mathrm{y}} ^{\mathrm{2}} }=\sqrt{\mathrm{4}\pi^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \pi\mathrm{t}+\mathrm{256}\pi^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \pi\mathrm{tcos}\:^{\mathrm{2}} \pi\mathrm{t}} \\ $$$$\mathrm{V}\left(\mathrm{t}\right)=\mid\mathrm{2}\pi\mathrm{sin}\:\pi\mathrm{t}\sqrt{\mathrm{1}+\mathrm{64cos}\:^{\mathrm{2}} \pi\mathrm{t}}\mid \\ $$$$ \\ $$$$\mathrm{A}\left(\mathrm{t}\right)=\sqrt{\mathrm{A}_{\mathrm{x}} ^{\mathrm{2}} +\mathrm{A}_{\mathrm{y}} ^{\mathrm{2}} }=\sqrt{\mathrm{4}\pi^{\mathrm{4}} \mathrm{cos}\:^{\mathrm{2}} \pi\mathrm{t}+\mathrm{256}\pi^{\mathrm{4}} \left(\mathrm{2cos}\:^{\mathrm{2}} \pi\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{A}\left(\mathrm{t}\right)=\mathrm{2}\pi^{\mathrm{2}} \sqrt{\mathrm{cos}\:^{\mathrm{2}} \pi\mathrm{t}+\mathrm{64}\left(\mathrm{4cos}\:^{\mathrm{4}} \pi\mathrm{t}−\mathrm{4cos}\:^{\mathrm{2}} \pi\mathrm{t}+\mathrm{1}\right)} \\ $$$$\mathrm{A}\left(\mathrm{t}\right)=\mathrm{2}\pi^{\mathrm{2}} \sqrt{\mathrm{256cos}\:^{\mathrm{4}} \pi\mathrm{t}−\mathrm{255cos}\:^{\mathrm{2}} \pi\mathrm{t}+\mathrm{64}} \\ $$$$ \\ $$$$\mathrm{at}\:\mathrm{t}=\mathrm{0}: \\ $$$$\mathrm{sin}\:\pi\mathrm{t}=\mathrm{sin}\:\mathrm{0}=\mathrm{0} \\ $$$$\mathrm{cos}\:\pi\mathrm{t}=\mathrm{cos}\:\mathrm{0}=\mathrm{1} \\ $$$$\mathrm{V}\left(\mathrm{t}\right)=\mathrm{0}\:\mathrm{m}/\mathrm{s} \\ $$$$\mathrm{A}\left(\mathrm{t}\right)=\mathrm{2}\pi^{\mathrm{2}} \sqrt{\mathrm{256}−\mathrm{255}+\mathrm{64}}=\mathrm{2}\pi^{\mathrm{2}} \sqrt{\mathrm{65}}\:\:\mathrm{m}/\mathrm{s}^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{at}\:\mathrm{t}=\mathrm{1}.\mathrm{5}\:\mathrm{s}: \\ $$$$\mathrm{sin}\:\pi\mathrm{t}=\mathrm{sin}\:\frac{\mathrm{3}\pi}{\mathrm{2}}=−\mathrm{1} \\ $$$$\mathrm{cos}\:\pi\mathrm{t}=\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{V}\left(\mathrm{t}\right)=\mathrm{2}\pi\:\:\mathrm{m}/\mathrm{s} \\ $$$$\mathrm{A}\left(\mathrm{t}\right)=\mathrm{2}\pi^{\mathrm{2}} \sqrt{\mathrm{64}}=\mathrm{16}\pi^{\mathrm{2}} \:\:\mathrm{m}/\mathrm{s}^{\mathrm{2}} \\ $$
Commented by tawakalitu last updated on 26/Nov/16
Thank you sir. God bless you.
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Commented by tawakalitu last updated on 26/Nov/16
i really appreciate.
$$\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *