Question Number 9594 by tawakalitu last updated on 19/Dec/16

Answered by sandy_suhendra last updated on 20/Dec/16

Commented by tawakalitu last updated on 20/Dec/16

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by tawakalitu last updated on 20/Dec/16

$$\mathrm{Thanks}\:\mathrm{but}\:\mathrm{please}\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{answer}\:? \\ $$
Commented by sandy_suhendra last updated on 20/Dec/16
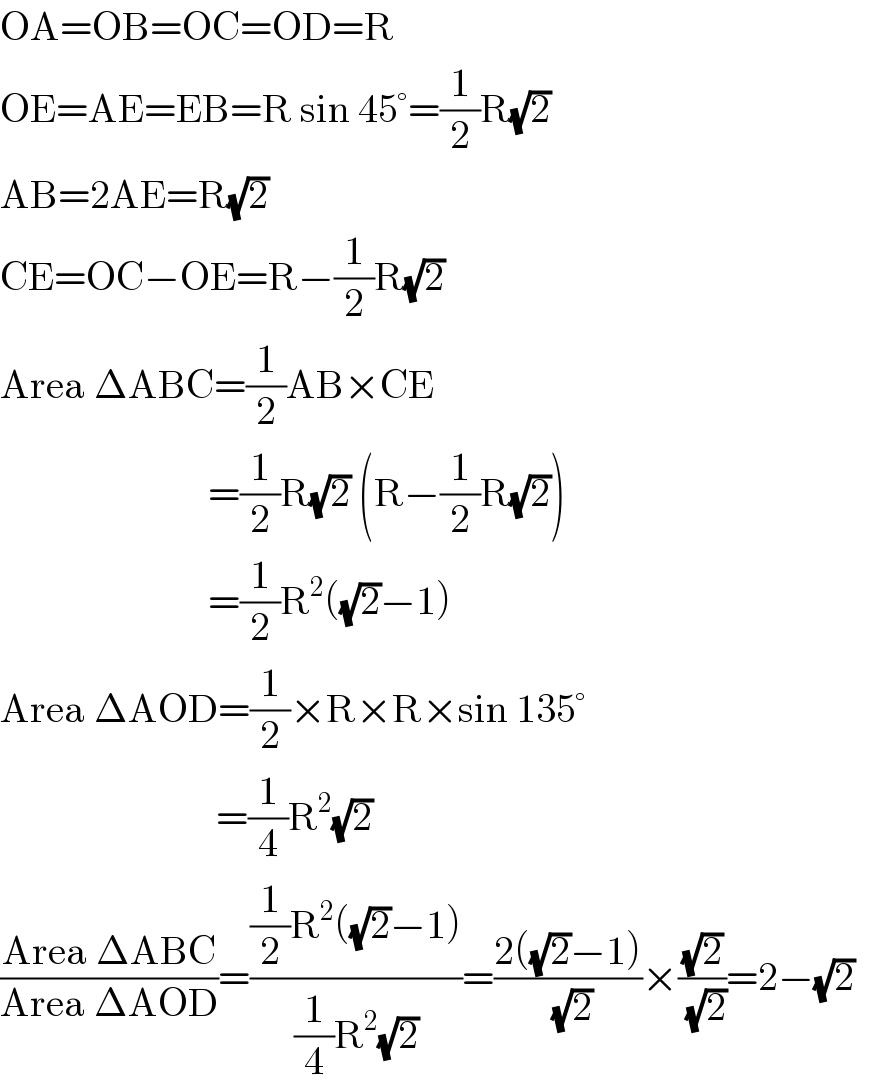
$$\mathrm{OA}=\mathrm{OB}=\mathrm{OC}=\mathrm{OD}=\mathrm{R} \\ $$$$\mathrm{OE}=\mathrm{AE}=\mathrm{EB}=\mathrm{R}\:\mathrm{sin}\:\mathrm{45}°=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{R}\sqrt{\mathrm{2}} \\ $$$$\mathrm{AB}=\mathrm{2AE}=\mathrm{R}\sqrt{\mathrm{2}} \\ $$$$\mathrm{CE}=\mathrm{OC}−\mathrm{OE}=\mathrm{R}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{R}\sqrt{\mathrm{2}} \\ $$$$\mathrm{Area}\:\Delta\mathrm{ABC}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{AB}×\mathrm{CE} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{R}\sqrt{\mathrm{2}}\:\left(\mathrm{R}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{R}\sqrt{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{R}^{\mathrm{2}} \left(\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$$\mathrm{Area}\:\Delta\mathrm{AOD}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{R}×\mathrm{R}×\mathrm{sin}\:\mathrm{135}° \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{R}^{\mathrm{2}} \sqrt{\mathrm{2}} \\ $$$$\frac{\mathrm{Area}\:\Delta\mathrm{ABC}}{\mathrm{Area}\:\Delta\mathrm{AOD}}=\frac{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{R}^{\mathrm{2}} \left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\frac{\mathrm{1}}{\mathrm{4}}\mathrm{R}^{\mathrm{2}} \sqrt{\mathrm{2}}}=\frac{\mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\:\sqrt{\mathrm{2}}}×\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}}=\mathrm{2}−\sqrt{\mathrm{2}}\:\:\: \\ $$
