Question Number 9617 by tawakalitu last updated on 20/Dec/16

Commented by sou1618 last updated on 21/Dec/16
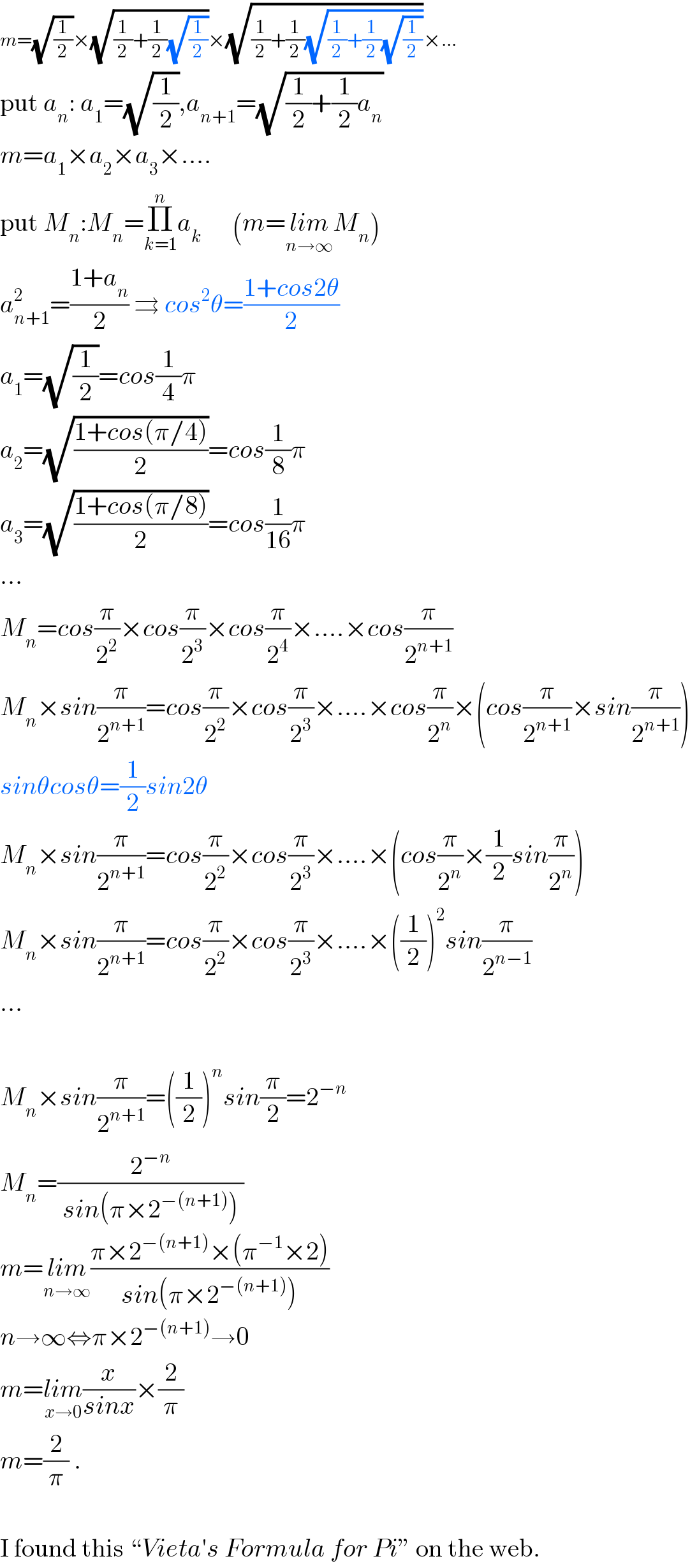
$${m}=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}×\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}}×\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}}}×… \\ $$$$\mathrm{put}\:{a}_{{n}} :\:{a}_{\mathrm{1}} =\sqrt{\frac{\mathrm{1}}{\mathrm{2}}},{a}_{{n}+\mathrm{1}} =\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{a}_{{n}} } \\ $$$${m}={a}_{\mathrm{1}} ×{a}_{\mathrm{2}} ×{a}_{\mathrm{3}} ×…. \\ $$$$\mathrm{put}\:{M}_{{n}} :{M}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{a}_{{k}} \:\:\:\:\:\:\left({m}=\underset{{n}\rightarrow\infty} {{lim}M}_{{n}} \right) \\ $$$${a}_{{n}+\mathrm{1}} ^{\mathrm{2}} =\frac{\mathrm{1}+{a}_{{n}} }{\mathrm{2}}\:\rightrightarrows\:{cos}^{\mathrm{2}} \theta=\frac{\mathrm{1}+{cos}\mathrm{2}\theta}{\mathrm{2}} \\ $$$${a}_{\mathrm{1}} =\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}={cos}\frac{\mathrm{1}}{\mathrm{4}}\pi \\ $$$${a}_{\mathrm{2}} =\sqrt{\frac{\mathrm{1}+{cos}\left(\pi/\mathrm{4}\right)}{\mathrm{2}}}={cos}\frac{\mathrm{1}}{\mathrm{8}}\pi \\ $$$${a}_{\mathrm{3}} =\sqrt{\frac{\mathrm{1}+{cos}\left(\pi/\mathrm{8}\right)}{\mathrm{2}}}={cos}\frac{\mathrm{1}}{\mathrm{16}}\pi \\ $$$$… \\ $$$${M}_{{n}} ={cos}\frac{\pi}{\mathrm{2}^{\mathrm{2}} }×{cos}\frac{\pi}{\mathrm{2}^{\mathrm{3}} }×{cos}\frac{\pi}{\mathrm{2}^{\mathrm{4}} }×….×{cos}\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} } \\ $$$${M}_{{n}} ×{sin}\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }={cos}\frac{\pi}{\mathrm{2}^{\mathrm{2}} }×{cos}\frac{\pi}{\mathrm{2}^{\mathrm{3}} }×….×{cos}\frac{\pi}{\mathrm{2}^{{n}} }×\left({cos}\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }×{sin}\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }\right) \\ $$$${sin}\theta{cos}\theta=\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{2}\theta \\ $$$${M}_{{n}} ×{sin}\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }={cos}\frac{\pi}{\mathrm{2}^{\mathrm{2}} }×{cos}\frac{\pi}{\mathrm{2}^{\mathrm{3}} }×….×\left({cos}\frac{\pi}{\mathrm{2}^{{n}} }×\frac{\mathrm{1}}{\mathrm{2}}{sin}\frac{\pi}{\mathrm{2}^{{n}} }\right) \\ $$$${M}_{{n}} ×{sin}\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }={cos}\frac{\pi}{\mathrm{2}^{\mathrm{2}} }×{cos}\frac{\pi}{\mathrm{2}^{\mathrm{3}} }×….×\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} {sin}\frac{\pi}{\mathrm{2}^{{n}−\mathrm{1}} } \\ $$$$… \\ $$$$ \\ $$$${M}_{{n}} ×{sin}\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }=\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} {sin}\frac{\pi}{\mathrm{2}}=\mathrm{2}^{−{n}} \\ $$$${M}_{{n}} =\frac{\mathrm{2}^{−{n}} }{\:{sin}\left(\pi×\mathrm{2}^{−\left({n}+\mathrm{1}\right)} \right)\:} \\ $$$${m}=\underset{{n}\rightarrow\infty} {{lim}}\frac{\pi×\mathrm{2}^{−\left({n}+\mathrm{1}\right)} ×\left(\pi^{−\mathrm{1}} ×\mathrm{2}\right)}{\:{sin}\left(\pi×\mathrm{2}^{−\left({n}+\mathrm{1}\right)} \right)\:} \\ $$$${n}\rightarrow\infty\Leftrightarrow\pi×\mathrm{2}^{−\left({n}+\mathrm{1}\right)} \rightarrow\mathrm{0} \\ $$$${m}=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{x}}{{sinx}}×\frac{\mathrm{2}}{\pi} \\ $$$${m}=\frac{\mathrm{2}}{\pi}\:. \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{found}\:\mathrm{this}\:“{Vieta}'{s}\:{Formula}\:{for}\:{Pi}''\:\mathrm{on}\:\mathrm{the}\:\mathrm{web}. \\ $$
Commented by tawakalitu last updated on 21/Dec/16

$$\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort}\:\mathrm{sir}. \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
