Question Number 9699 by ridwan balatif last updated on 26/Dec/16

Commented by ridwan balatif last updated on 26/Dec/16
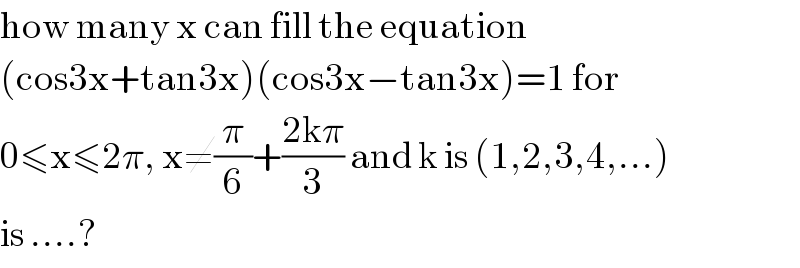
$$\mathrm{how}\:\mathrm{many}\:\mathrm{x}\:\mathrm{can}\:\mathrm{fill}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\left(\mathrm{cos3x}+\mathrm{tan3x}\right)\left(\mathrm{cos3x}−\mathrm{tan3x}\right)=\mathrm{1}\:\mathrm{for} \\ $$$$\mathrm{0}\leqslant\mathrm{x}\leqslant\mathrm{2}\pi,\:\mathrm{x}\neq\frac{\pi}{\mathrm{6}}+\frac{\mathrm{2k}\pi}{\mathrm{3}}\:\mathrm{and}\:\mathrm{k}\:\mathrm{is}\:\left(\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},…\right)\: \\ $$$$\mathrm{is}\:….? \\ $$
Commented by sou1618 last updated on 26/Dec/16
![(cos3x+tan3x)(cos3x−tan3x)=1 cos^2 3x−tan^2 3x−1=0 cos^2 3x−(((sin^2 3x)/(cos^2 3x))+1)=0 cos^2 3x−((sin^2 3x+cos^2 3x)/(cos^2 3x))=0 cos^2 3x=(1/(cos^2 3x)) ∗cos3x≠0 ⇔[x≠((1/6)+(2/3)k)π] cos^2 3x×cos^2 3x=1 cos3x=±1 3x=0,π,2π,3π......=nπ (n=0,1,2....) x=(1/3)nπ 0≤x≤2π x=0,(1/3)π,(2/3)π, π,(4/3)π,(5/3)π, 2π (Ans)=8](https://www.tinkutara.com/question/Q9701.png)
$$\left({cos}\mathrm{3}{x}+{tan}\mathrm{3}{x}\right)\left({cos}\mathrm{3}{x}−{tan}\mathrm{3}{x}\right)=\mathrm{1} \\ $$$${cos}^{\mathrm{2}} \mathrm{3}{x}−{tan}^{\mathrm{2}} \mathrm{3}{x}−\mathrm{1}=\mathrm{0} \\ $$$${cos}^{\mathrm{2}} \mathrm{3}{x}−\left(\frac{{sin}^{\mathrm{2}} \mathrm{3}{x}}{{cos}^{\mathrm{2}} \mathrm{3}{x}}+\mathrm{1}\right)=\mathrm{0} \\ $$$${cos}^{\mathrm{2}} \mathrm{3}{x}−\frac{{sin}^{\mathrm{2}} \mathrm{3}{x}+{cos}^{\mathrm{2}} \mathrm{3}{x}}{{cos}^{\mathrm{2}} \mathrm{3}{x}}=\mathrm{0} \\ $$$${cos}^{\mathrm{2}} \mathrm{3}{x}=\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \mathrm{3}{x}} \\ $$$$\ast{cos}\mathrm{3}{x}\neq\mathrm{0}\:\Leftrightarrow\left[{x}\neq\left(\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{2}}{\mathrm{3}}{k}\right)\pi\right] \\ $$$$\:\:{cos}^{\mathrm{2}} \mathrm{3}{x}×{cos}^{\mathrm{2}} \mathrm{3}{x}=\mathrm{1} \\ $$$$\:\:{cos}\mathrm{3}{x}=\pm\mathrm{1} \\ $$$$\:\:\:\:\mathrm{3}{x}=\mathrm{0},\pi,\mathrm{2}\pi,\mathrm{3}\pi……={n}\pi\:\left({n}=\mathrm{0},\mathrm{1},\mathrm{2}….\right) \\ $$$$\:\:\:\:{x}=\frac{\mathrm{1}}{\mathrm{3}}{n}\pi \\ $$$$\mathrm{0}\leqslant{x}\leqslant\mathrm{2}\pi \\ $$$$\:\:{x}=\mathrm{0},\frac{\mathrm{1}}{\mathrm{3}}\pi,\frac{\mathrm{2}}{\mathrm{3}}\pi,\:\pi,\frac{\mathrm{4}}{\mathrm{3}}\pi,\frac{\mathrm{5}}{\mathrm{3}}\pi,\:\mathrm{2}\pi \\ $$$$\left({Ans}\right)=\mathrm{8}\: \\ $$
Commented by ridwan balatif last updated on 26/Dec/16

$$\mathrm{okay},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{now}\:\mathrm{i}\:\mathrm{understand} \\ $$
