Question-9824

Question Number 9824 by j.masanja06@gmail.com last updated on 06/Jan/17

Answered by sandy_suhendra last updated on 06/Jan/17

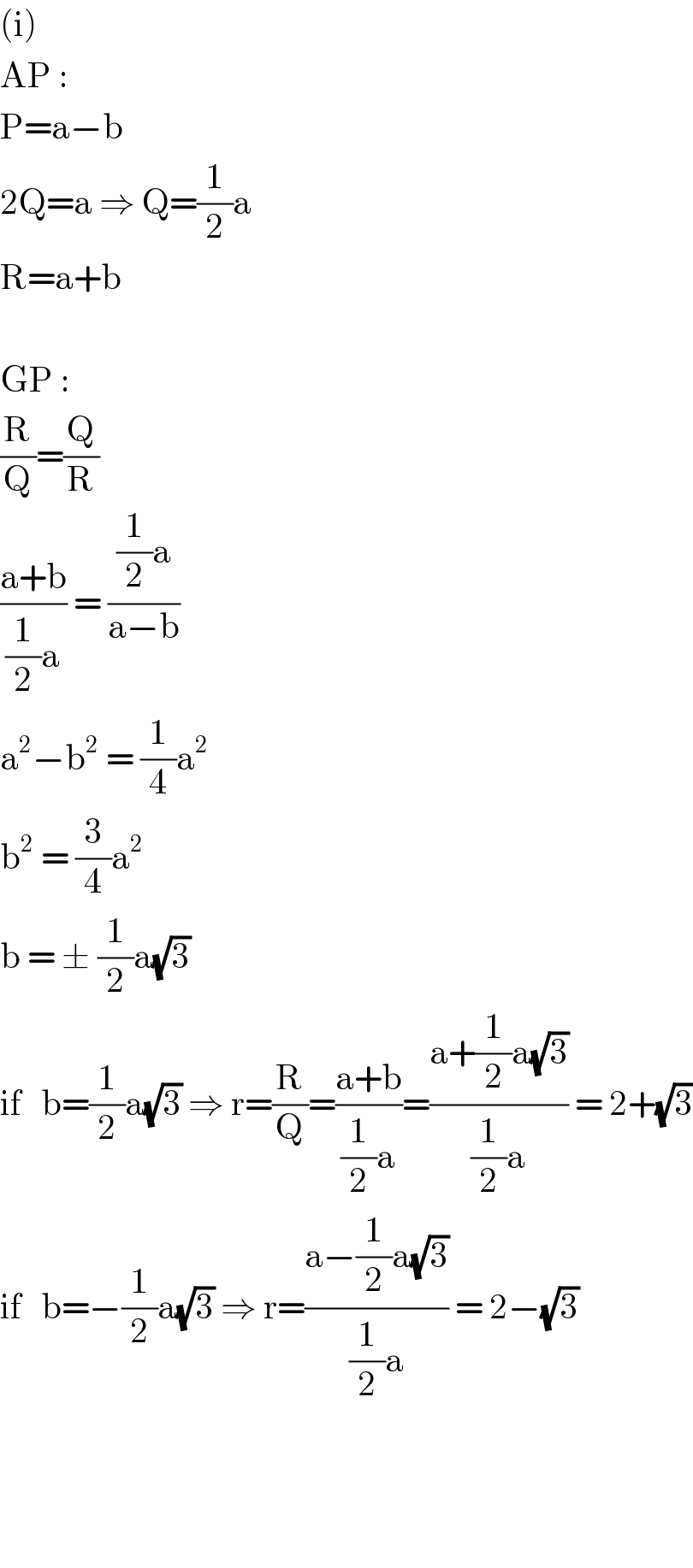
(i) AP : P=a−b 2Q=a ⇒ Q=(1/2)a R=a+b GP : (R/Q)=(Q/R) ((a+b)/((1/2)a)) = (((1/2)a)/(a−b)) a^2 −b^2 = (1/4)a^2 b^2 = (3/4)a^2 b = ± (1/2)a(√3) if b=(1/2)a(√3) ⇒ r=(R/Q)=((a+b)/((1/2)a))=((a+(1/2)a(√3))/((1/2)a)) = 2+(√3) if b=−(1/2)a(√3) ⇒ r=((a−(1/2)a(√3))/((1/2)a)) = 2−(√3)

$$\left(\mathrm{i}\right) \\ $$$$\mathrm{AP}\:: \\ $$$$\mathrm{P}=\mathrm{a}−\mathrm{b} \\ $$$$\mathrm{2Q}=\mathrm{a}\:\Rightarrow\:\mathrm{Q}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{a} \\ $$$$\mathrm{R}=\mathrm{a}+\mathrm{b} \\ $$$$ \\ $$$$\mathrm{GP}\:: \\ $$$$\frac{\mathrm{R}}{\mathrm{Q}}=\frac{\mathrm{Q}}{\mathrm{R}} \\ $$$$\frac{\mathrm{a}+\mathrm{b}}{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{a}}\:=\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{a}}{\mathrm{a}−\mathrm{b}} \\ $$$$\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{a}^{\mathrm{2}} \\ $$$$\mathrm{b}^{\mathrm{2}} \:=\:\frac{\mathrm{3}}{\mathrm{4}}\mathrm{a}^{\mathrm{2}} \\ $$$$\mathrm{b}\:=\:\pm\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{a}\sqrt{\mathrm{3}} \\ $$$$\mathrm{if}\:\:\:\mathrm{b}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{a}\sqrt{\mathrm{3}}\:\Rightarrow\:\mathrm{r}=\frac{\mathrm{R}}{\mathrm{Q}}=\frac{\mathrm{a}+\mathrm{b}}{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{a}}=\frac{\mathrm{a}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{a}\sqrt{\mathrm{3}}}{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{a}}\:=\:\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$$\mathrm{if}\:\:\:\mathrm{b}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{a}\sqrt{\mathrm{3}}\:\Rightarrow\:\mathrm{r}=\frac{\mathrm{a}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{a}\sqrt{\mathrm{3}}}{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{a}}\:=\:\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Commented by j.masanja06@gmail.com last updated on 11/Jan/17

$$\mathrm{thanks}\:\mathrm{sir} \\ $$

Commented by sandy_suhendra last updated on 06/Jan/17

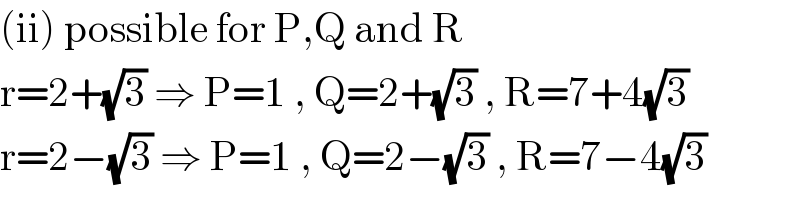
(ii) possible for P,Q and R r=2+(√3) ⇒ P=1 , Q=2+(√3) , R=7+4(√3) r=2−(√3) ⇒ P=1 , Q=2−(√3) , R=7−4(√3)

$$\left(\mathrm{ii}\right)\:\mathrm{possible}\:\mathrm{for}\:\mathrm{P},\mathrm{Q}\:\mathrm{and}\:\mathrm{R} \\ $$$$\mathrm{r}=\mathrm{2}+\sqrt{\mathrm{3}}\:\Rightarrow\:\mathrm{P}=\mathrm{1}\:,\:\mathrm{Q}=\mathrm{2}+\sqrt{\mathrm{3}}\:,\:\mathrm{R}=\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}} \\ $$$$\mathrm{r}=\mathrm{2}−\sqrt{\mathrm{3}}\:\Rightarrow\:\mathrm{P}=\mathrm{1}\:,\:\mathrm{Q}=\mathrm{2}−\sqrt{\mathrm{3}}\:,\:\mathrm{R}=\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply