Question Number 9847 by 0942679167 last updated on 07/Jan/17

Commented by prakash jain last updated on 08/Jan/17

$$\mathrm{Can}\:\mathrm{u}\:\mathrm{please}\:\mathrm{type}\:\mathrm{the}\:\mathrm{question} \\ $$$$\mathrm{image}\:\mathrm{is}\:\mathrm{not}\:\mathrm{readble}. \\ $$$$\mathrm{Or}\:\mathrm{use}\:\mathrm{app}\:\mathrm{like}\:\mathrm{camscanner}\:\mathrm{to} \\ $$$$\mathrm{take}\:\mathrm{the}\:\mathrm{image} \\ $$
Commented by FilupSmith last updated on 09/Jan/17
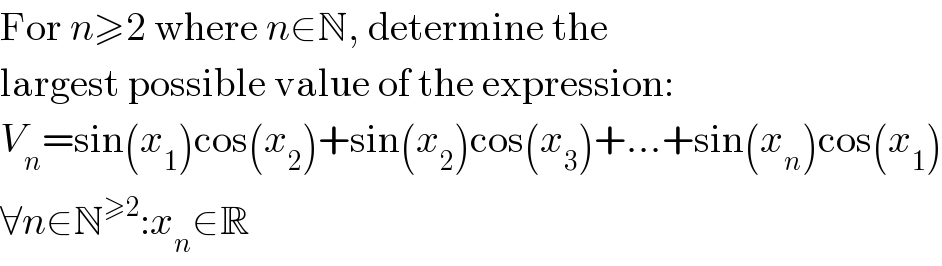
$$\mathrm{For}\:{n}\geqslant\mathrm{2}\:\mathrm{where}\:{n}\in\mathbb{N},\:\mathrm{determine}\:\mathrm{the} \\ $$$$\mathrm{largest}\:\mathrm{possible}\:\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{expression}: \\ $$$${V}_{{n}} =\mathrm{sin}\left({x}_{\mathrm{1}} \right)\mathrm{cos}\left({x}_{\mathrm{2}} \right)+\mathrm{sin}\left({x}_{\mathrm{2}} \right)\mathrm{cos}\left({x}_{\mathrm{3}} \right)+…+\mathrm{sin}\left({x}_{{n}} \right)\mathrm{cos}\left({x}_{\mathrm{1}} \right) \\ $$$$\forall{n}\in\mathbb{N}^{\geqslant\mathrm{2}} :{x}_{{n}} \in\mathbb{R} \\ $$
Commented by FilupSmith last updated on 09/Jan/17
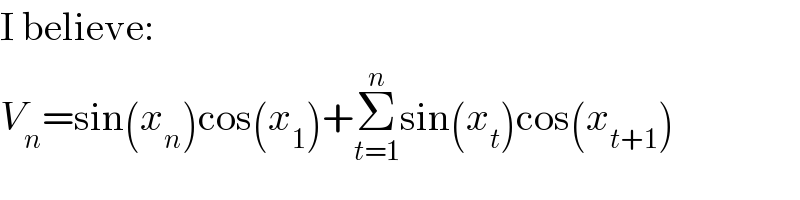
$$\mathrm{I}\:\mathrm{believe}: \\ $$$${V}_{{n}} =\mathrm{sin}\left({x}_{{n}} \right)\mathrm{cos}\left({x}_{\mathrm{1}} \right)+\underset{{t}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{sin}\left({x}_{{t}} \right)\mathrm{cos}\left({x}_{{t}+\mathrm{1}} \right) \\ $$
Answered by mrW1 last updated on 19/Jan/17
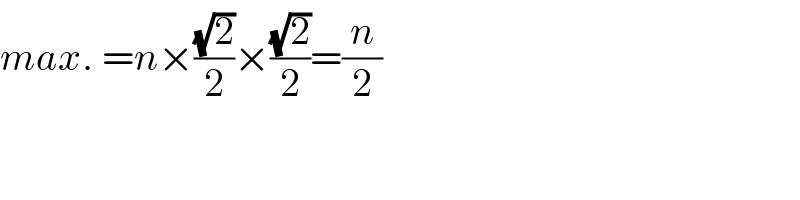
$${max}.\:={n}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}=\frac{{n}}{\mathrm{2}} \\ $$
