Question Number 9907 by amir last updated on 15/Jan/17

Commented by RasheedSoomro last updated on 15/Jan/17
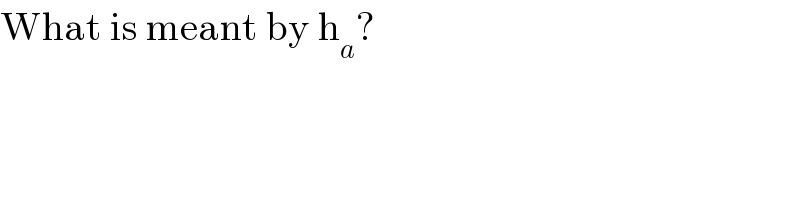
$$\mathrm{What}\:\mathrm{is}\:\mathrm{meant}\:\mathrm{by}\:\mathrm{h}_{{a}} ? \\ $$
Commented by amir last updated on 15/Jan/17

$${h}_{{a}} \:{is}\:{the}\:{perpendicular}\:{line}\:{from}\:{A}\:{point}\:{to}\:{BC}\:{side}. \\ $$
Answered by mrW1 last updated on 21/Jan/17

$$\Delta{ABC}\:{with}\:{sides}\:{a},{b},{c}\:{and}\:{area}\:{S}. \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×{a}×{h}_{{a}} ={S} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{h}_{{a}} }=\frac{{a}}{\mathrm{2}{S}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×{b}×{h}_{{b}} ={S} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{h}_{{b}} }=\frac{{b}}{\mathrm{2}{S}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×{c}×{h}_{{c}} ={S} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{h}_{{c}} }=\frac{{c}}{\mathrm{2}{S}} \\ $$$${it}\:{means}\:{the}\:{new}\:{triangle}\:{with}\:{the}\:{sides}\:{of} \\ $$$$\frac{\mathrm{1}}{{h}_{{a}} },\frac{\mathrm{1}}{{h}_{{b}} },\frac{\mathrm{1}}{{h}_{{c}} }\:{is}\:{similar}\:{with}\:{the}\:{original}\:{triangle} \\ $$$${with}\:{the}\:{sides}\:{of}\:{a},{b},{c}. \\ $$$${the}\:{ratio}\:{of}\:{the}\:{corresponding}\:{sides} \\ $$$${is}\:\frac{\mathrm{1}}{\mathrm{2}{S}}. \\ $$$$ \\ $$$${the}\:{ratio}\:{of}\:{the}\:{areas}\:{of}\:{both}\:{triangles} \\ $$$${is}\:{the}\:{square}\:{of}\:{the}\:{ratio}\:{of}\:{their}\:{sides}. \\ $$$$\Rightarrow\frac{{S}_{\mathrm{1}} }{{S}}=\left(\frac{\mathrm{1}}{\mathrm{2}{S}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}{S}^{\mathrm{2}} } \\ $$$$\Rightarrow{S}\centerdot{S}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by amir last updated on 29/Jan/17
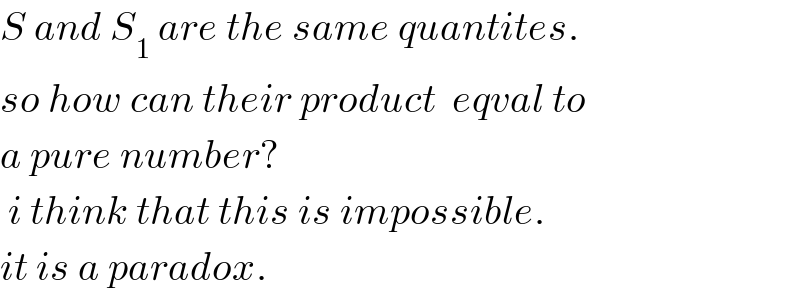
$${S}\:{and}\:{S}_{\mathrm{1}} \:{are}\:{the}\:{same}\:{quantites}. \\ $$$${so}\:{how}\:{can}\:{their}\:{product}\:\:{eqval}\:{to} \\ $$$${a}\:{pure}\:{number}? \\ $$$$\:{i}\:{think}\:{that}\:{this}\:{is}\:{impossible}. \\ $$$${it}\:{is}\:{a}\:{paradox}. \\ $$
