Question Number 9908 by ridwan balatif last updated on 15/Jan/17

Commented by ridwan balatif last updated on 15/Jan/17

$$\:\mathrm{x}\:\mathrm{maximum}\:=…? \\ $$
Answered by mrW1 last updated on 15/Jan/17
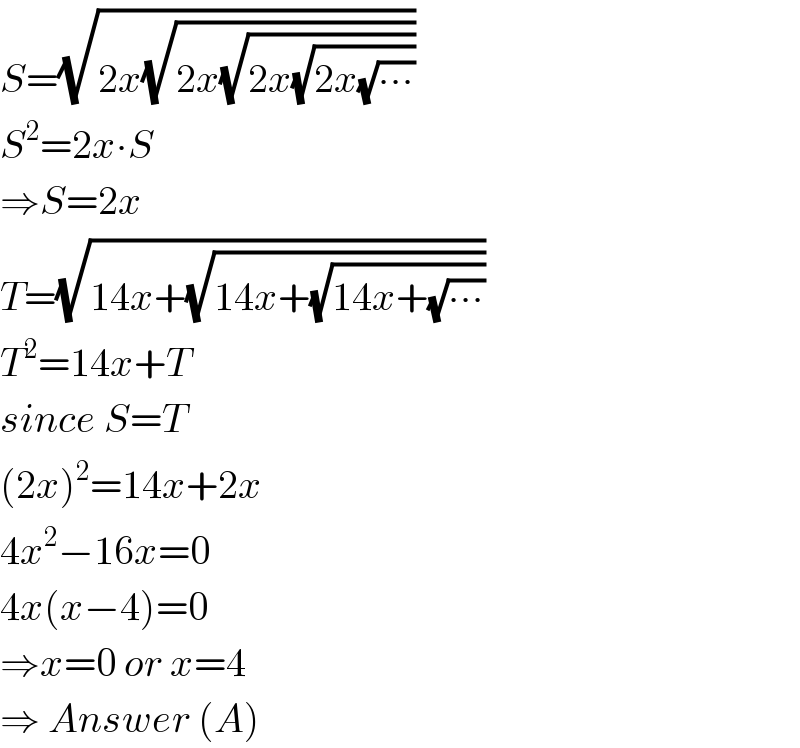
$${S}=\sqrt{\mathrm{2}{x}\sqrt{\mathrm{2}{x}\sqrt{\mathrm{2}{x}\sqrt{\mathrm{2}{x}\sqrt{\centerdot\centerdot\centerdot}}}}} \\ $$$${S}^{\mathrm{2}} =\mathrm{2}{x}\centerdot{S} \\ $$$$\Rightarrow{S}=\mathrm{2}{x} \\ $$$${T}=\sqrt{\mathrm{14}{x}+\sqrt{\mathrm{14}{x}+\sqrt{\mathrm{14}{x}+\sqrt{\centerdot\centerdot\centerdot}}}} \\ $$$${T}^{\mathrm{2}} =\mathrm{14}{x}+{T} \\ $$$${since}\:{S}={T} \\ $$$$\left(\mathrm{2}{x}\right)^{\mathrm{2}} =\mathrm{14}{x}+\mathrm{2}{x} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16}{x}=\mathrm{0} \\ $$$$\mathrm{4}{x}\left({x}−\mathrm{4}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{0}\:{or}\:{x}=\mathrm{4} \\ $$$$\Rightarrow\:{Answer}\:\left({A}\right) \\ $$
Commented by ridwan balatif last updated on 15/Jan/17

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
