Question Number 9912 by ridwan balatif last updated on 15/Jan/17
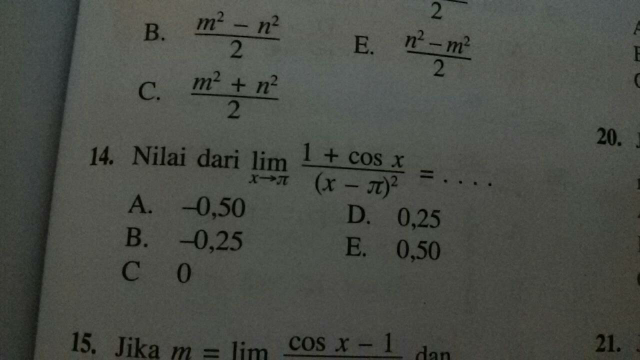
Answered by mrW1 last updated on 15/Jan/17
![lim_(x→π) ((1+cos x)/((x−π)^2 )) t=x−π x=t+π 1+cos x=1+cos (t+π)=1−cos t =1−(1−2sin^2 (t/2))=2sin^2 ((t/2)) lim_(x→π) ((1+cos x)/((x−π)^2 ))=lim_(t→0) ((2sin^2 ((t/2)) )/t^2 )=(1/2)×lim_(t→0) [((sin ((t/2)) )/(((t/2))))]^2 =(1/2)×1^2 =(1/2) ⇒ Answer (E)](https://www.tinkutara.com/question/Q9919.png)
$$\underset{{x}\rightarrow\pi} {\mathrm{lim}}\:\frac{\mathrm{1}+\mathrm{cos}\:{x}}{\left({x}−\pi\right)^{\mathrm{2}} } \\ $$$${t}={x}−\pi \\ $$$${x}={t}+\pi \\ $$$$\mathrm{1}+\mathrm{cos}\:{x}=\mathrm{1}+\mathrm{cos}\:\left({t}+\pi\right)=\mathrm{1}−\mathrm{cos}\:{t} \\ $$$$=\mathrm{1}−\left(\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \:\frac{{t}}{\mathrm{2}}\right)=\mathrm{2sin}^{\mathrm{2}} \left(\frac{{t}}{\mathrm{2}}\right)\: \\ $$$$\underset{{x}\rightarrow\pi} {\mathrm{lim}}\:\frac{\mathrm{1}+\mathrm{cos}\:{x}}{\left({x}−\pi\right)^{\mathrm{2}} }=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2sin}^{\mathrm{2}} \left(\frac{{t}}{\mathrm{2}}\right)\:}{{t}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}×\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\frac{\mathrm{sin}\:\left(\frac{{t}}{\mathrm{2}}\right)\:}{\left(\frac{{t}}{\mathrm{2}}\right)}\right]^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{1}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:{Answer}\:\left({E}\right) \\ $$
