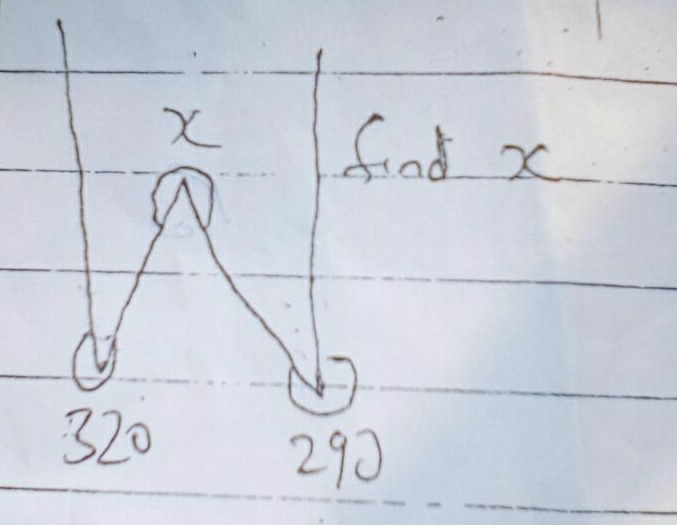
Question Number 9920 by Tawakalitu ayo mi last updated on 15/Jan/17
Answered by mrW1 last updated on 16/Jan/17
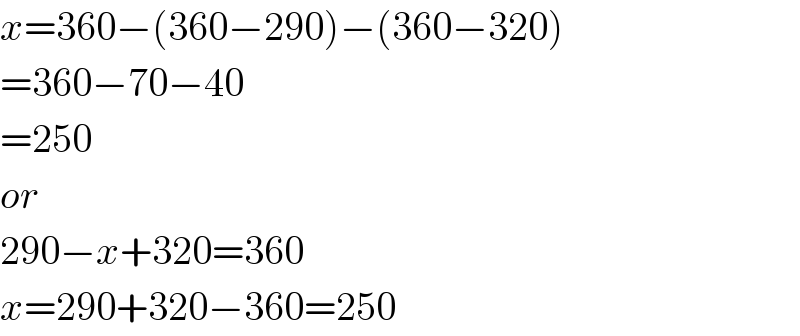
$${x}=\mathrm{360}−\left(\mathrm{360}−\mathrm{290}\right)−\left(\mathrm{360}−\mathrm{320}\right) \\ $$$$=\mathrm{360}−\mathrm{70}−\mathrm{40} \\ $$$$=\mathrm{250} \\ $$$${or} \\ $$$$\mathrm{290}−{x}+\mathrm{320}=\mathrm{360} \\ $$$${x}=\mathrm{290}+\mathrm{320}−\mathrm{360}=\mathrm{250} \\ $$
Commented by Tawakalitu ayo mi last updated on 16/Jan/17
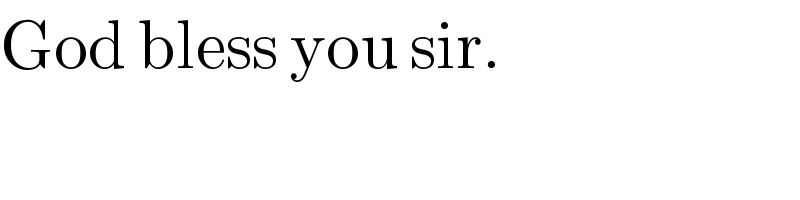
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by RasheedSoomro last updated on 16/Jan/17
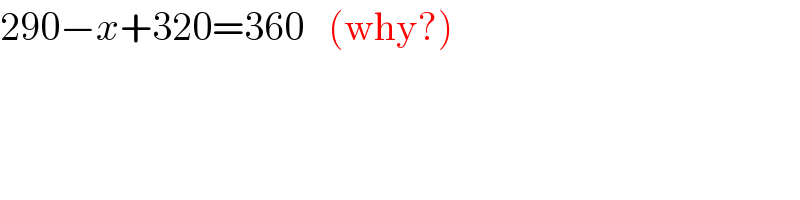
$$\mathrm{290}−{x}+\mathrm{320}=\mathrm{360}\:\:\:\left(\mathrm{why}?\right) \\ $$$$ \\ $$
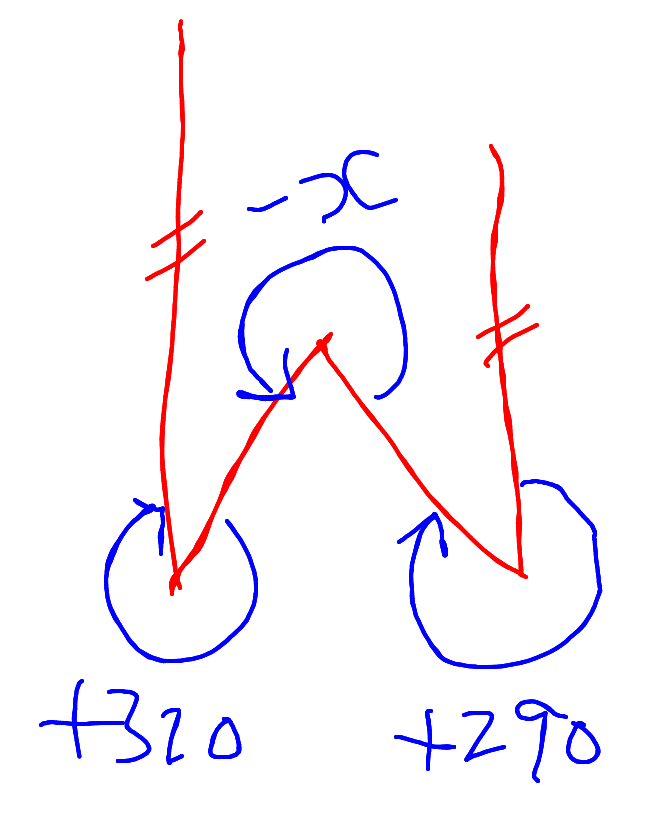
Commented by mrW1 last updated on 16/Jan/17

$${explanation}: \\ $$$${you}\:{go}\:{ahead},\:{turn}\:\mathrm{290}\:{degrees} \\ $$$${to}\:{the}\:{right}\:\left(+\right),\:{then}\:{turn}\:{x}\:{degrees} \\ $$$${to}\:{the}\:{left}\:\left(−\right)\:{and}\:{then}\:{turn}\:\mathrm{320}\:{degrees} \\ $$$${to}\:{the}\:{right}\:\left(+\right),\:{finally}\:{you}\:{are}\:{in}\: \\ $$$${your}\:{original}\:{direction}\:{again}, \\ $$$${it}\:{means}\:{tatally}\:{you}\:{turn}\:\mathrm{360}\:{degrees}. \\ $$$${i}.{e}.\:\mathrm{290}−{x}+\mathrm{320}=\mathrm{360} \\ $$
Commented by mrW1 last updated on 16/Jan/17
Commented by RasheedSoomro last updated on 17/Jan/17

$$\mathrm{You}\:\mathrm{supposed}\:\mathrm{the}\:\mathrm{legs}\:\mathrm{of}\:'\mathrm{W}' \\ $$$$\mathrm{to}\:\mathrm{be}\:\mathrm{parallel}\:\mathrm{whereas}\:\mathrm{I}\:\mathrm{didn}'\mathrm{t}. \\ $$$$\mathrm{Anyway}\:\mathrm{thanks}\:\mathrm{for}\:\mathrm{explanation}. \\ $$$$ \\ $$
