Question Number 9929 by ridwan balatif last updated on 16/Jan/17

Answered by mrW1 last updated on 18/Jan/17
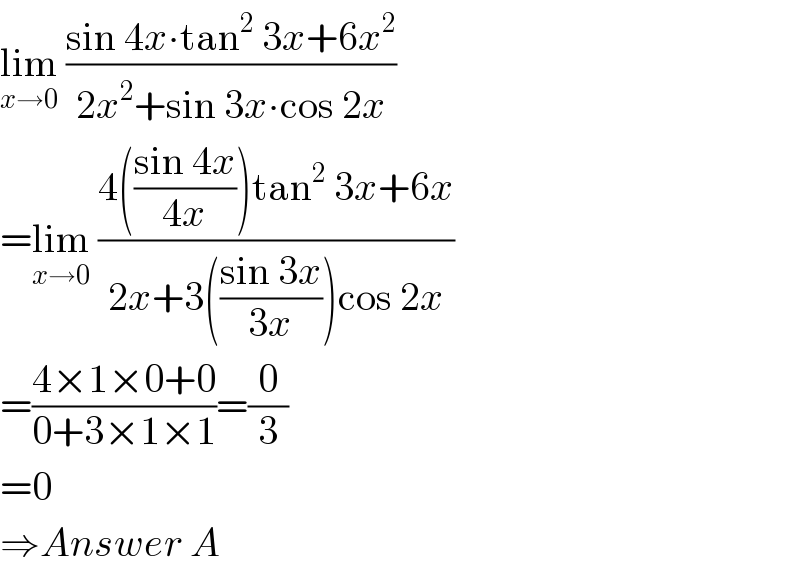
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{4}{x}\centerdot\mathrm{tan}^{\mathrm{2}} \:\mathrm{3}{x}+\mathrm{6}{x}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{sin}\:\mathrm{3}{x}\centerdot\mathrm{cos}\:\mathrm{2}{x}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{4}\left(\frac{\mathrm{sin}\:\mathrm{4}{x}}{\mathrm{4}{x}}\right)\mathrm{tan}^{\mathrm{2}} \:\mathrm{3}{x}+\mathrm{6}{x}}{\mathrm{2}{x}+\mathrm{3}\left(\frac{\mathrm{sin}\:\mathrm{3}{x}}{\mathrm{3}{x}}\right)\mathrm{cos}\:\mathrm{2}{x}} \\ $$$$=\frac{\mathrm{4}×\mathrm{1}×\mathrm{0}+\mathrm{0}}{\mathrm{0}+\mathrm{3}×\mathrm{1}×\mathrm{1}}=\frac{\mathrm{0}}{\mathrm{3}} \\ $$$$=\mathrm{0} \\ $$$$\Rightarrow{Answer}\:{A} \\ $$
Commented by ridwan balatif last updated on 18/Jan/17

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
