Question Number 9977 by konen last updated on 20/Jan/17
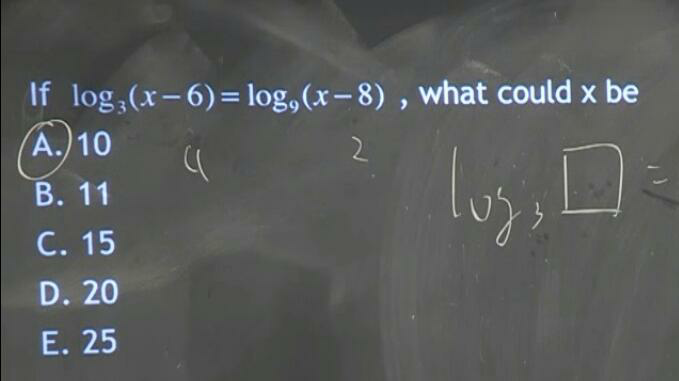
Answered by sandy_suhendra last updated on 20/Jan/17
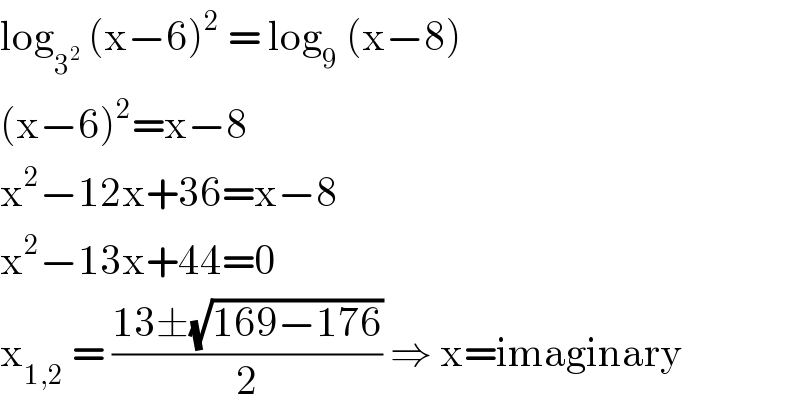
$$\mathrm{log}_{\mathrm{3}^{\mathrm{2}} } \:\left(\mathrm{x}−\mathrm{6}\right)^{\mathrm{2}} \:=\:\mathrm{log}_{\mathrm{9}} \:\left(\mathrm{x}−\mathrm{8}\right) \\ $$$$\left(\mathrm{x}−\mathrm{6}\right)^{\mathrm{2}} =\mathrm{x}−\mathrm{8} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{12x}+\mathrm{36}=\mathrm{x}−\mathrm{8} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{13x}+\mathrm{44}=\mathrm{0} \\ $$$$\mathrm{x}_{\mathrm{1},\mathrm{2}} \:=\:\frac{\mathrm{13}\pm\sqrt{\mathrm{169}−\mathrm{176}}}{\mathrm{2}}\:\Rightarrow\:\mathrm{x}=\mathrm{imaginary} \\ $$
Commented by prakash jain last updated on 20/Jan/17
![If the question was log _9 (x−6)=log_3 (x−8) (x−6)=(x−8)^2 x−6=x^2 −16x+64 x^2 −17x+70=0 (x−7)(x−10)=0 x=10 [x=7 does not satisfy]](https://www.tinkutara.com/question/Q9985.png)
$$\mathrm{If}\:\mathrm{the}\:\mathrm{question}\:\mathrm{was} \\ $$$$\mathrm{log}\:_{\mathrm{9}} \left({x}−\mathrm{6}\right)=\mathrm{log}_{\mathrm{3}} \left({x}−\mathrm{8}\right) \\ $$$$\left({x}−\mathrm{6}\right)=\left({x}−\mathrm{8}\right)^{\mathrm{2}} \\ $$$${x}−\mathrm{6}={x}^{\mathrm{2}} −\mathrm{16}{x}+\mathrm{64} \\ $$$${x}^{\mathrm{2}} −\mathrm{17}{x}+\mathrm{70}=\mathrm{0} \\ $$$$\left({x}−\mathrm{7}\right)\left({x}−\mathrm{10}\right)=\mathrm{0} \\ $$$${x}=\mathrm{10}\:\left[{x}=\mathrm{7}\:\mathrm{does}\:\mathrm{not}\:\mathrm{satisfy}\right] \\ $$
