Menu Close

Question-figure-x-for-x-4-gt-6-x-my-answer-1-x-4-gt-6-x-2-x-5-x-8-lt-0-5-lt-x-lt-8-2-x-4-0-x-4-so-I-have-for-x-5-lt-x-lt-8-what-s-wr

Tinku Tara 0 Comments
Pin




Question Number 8234 by sandy_suhendra last updated on 03/Oct/16
Question : figure x for (√(x−4)) > 6−x my answer : (1) x−4 > (6−x)^2 (x−5)(x−8) < 0 5<x<8 (2) x−4 ≥ 0 x ≥ 4 so I have for x ⇒ 5<x<8 what′s wrong with this answer, please help me because if x=9 ⇒ (√(9−4)) > 6−9 , it′s true
$$\mathrm{Question}\::\:\mathrm{figure}\:\mathrm{x}\:\mathrm{for} \\ $$$$\sqrt{\mathrm{x}−\mathrm{4}}\:>\:\mathrm{6}−\mathrm{x} \\ $$$$\mathrm{my}\:\mathrm{answer}\:: \\ $$$$\left(\mathrm{1}\right)\:\:\:\mathrm{x}−\mathrm{4}\:>\:\left(\mathrm{6}−\mathrm{x}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\left(\mathrm{x}−\mathrm{5}\right)\left(\mathrm{x}−\mathrm{8}\right)\:<\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{5}<\mathrm{x}<\mathrm{8} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:\:\:\mathrm{x}−\mathrm{4}\:\geqslant\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}\:\geqslant\:\mathrm{4} \\ $$$$\mathrm{so}\:\mathrm{I}\:\mathrm{have}\:\mathrm{for}\:\mathrm{x}\:\Rightarrow\:\mathrm{5}<\mathrm{x}<\mathrm{8} \\ $$$$\mathrm{what}'\mathrm{s}\:\mathrm{wrong}\:\mathrm{with}\:\mathrm{this}\:\mathrm{answer},\:\mathrm{please}\:\mathrm{help}\:\mathrm{me} \\ $$$$\mathrm{because}\:\mathrm{if}\:\mathrm{x}=\mathrm{9}\:\Rightarrow\:\sqrt{\mathrm{9}−\mathrm{4}}\:>\:\mathrm{6}−\mathrm{9}\:,\:\mathrm{it}'\mathrm{s}\:\mathrm{true} \\ $$
Commented by Rasheed Soomro last updated on 03/Oct/16
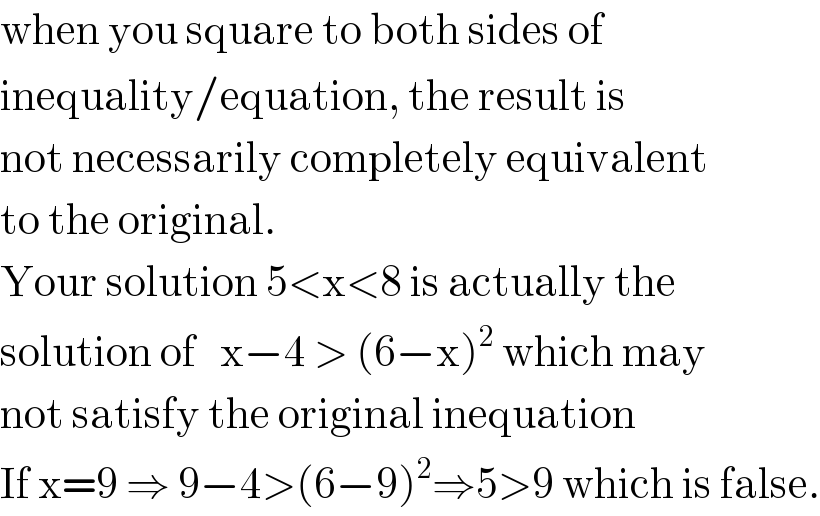
when you square to both sides of inequality/equation, the result is not necessarily completely equivalent to the original. Your solution 5<x<8 is actually the solution of x−4 > (6−x)^2 which may not satisfy the original inequation If x=9 ⇒ 9−4>(6−9)^2 ⇒5>9 which is false.
$$\mathrm{when}\:\mathrm{you}\:\mathrm{square}\:\mathrm{to}\:\mathrm{both}\:\mathrm{sides}\:\mathrm{of} \\ $$$$\mathrm{inequality}/\mathrm{equation},\:\mathrm{the}\:\mathrm{result}\:\mathrm{is} \\ $$$$\mathrm{not}\:\mathrm{necessarily}\:\mathrm{completely}\:\mathrm{equivalent} \\ $$$$\mathrm{to}\:\mathrm{the}\:\mathrm{original}. \\ $$$$\mathrm{Your}\:\mathrm{solution}\:\mathrm{5}<\mathrm{x}<\mathrm{8}\:\mathrm{is}\:\mathrm{actually}\:\mathrm{the} \\ $$$$\mathrm{solution}\:\mathrm{of}\:\:\:\mathrm{x}−\mathrm{4}\:>\:\left(\mathrm{6}−\mathrm{x}\right)^{\mathrm{2}} \:\mathrm{which}\:\mathrm{may} \\ $$$$\mathrm{not}\:\mathrm{satisfy}\:\mathrm{the}\:\mathrm{original}\:\mathrm{inequation} \\ $$$$\mathrm{If}\:\mathrm{x}=\mathrm{9}\:\Rightarrow\:\mathrm{9}−\mathrm{4}>\left(\mathrm{6}−\mathrm{9}\right)^{\mathrm{2}} \Rightarrow\mathrm{5}>\mathrm{9}\:\mathrm{which}\:\mathrm{is}\:\mathrm{false}. \\ $$
Commented by Yozzias last updated on 03/Oct/16
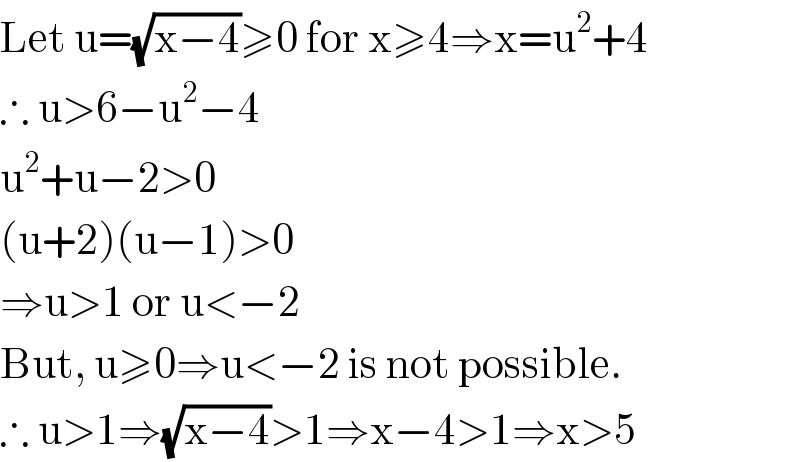
Let u=(√(x−4))≥0 for x≥4⇒x=u^2 +4 ∴ u>6−u^2 −4 u^2 +u−2>0 (u+2)(u−1)>0 ⇒u>1 or u<−2 But, u≥0⇒u<−2 is not possible. ∴ u>1⇒(√(x−4))>1⇒x−4>1⇒x>5
$$\mathrm{Let}\:\mathrm{u}=\sqrt{\mathrm{x}−\mathrm{4}}\geqslant\mathrm{0}\:\mathrm{for}\:\mathrm{x}\geqslant\mathrm{4}\Rightarrow\mathrm{x}=\mathrm{u}^{\mathrm{2}} +\mathrm{4} \\ $$$$\therefore\:\mathrm{u}>\mathrm{6}−\mathrm{u}^{\mathrm{2}} −\mathrm{4} \\ $$$$\mathrm{u}^{\mathrm{2}} +\mathrm{u}−\mathrm{2}>\mathrm{0} \\ $$$$\left(\mathrm{u}+\mathrm{2}\right)\left(\mathrm{u}−\mathrm{1}\right)>\mathrm{0} \\ $$$$\Rightarrow\mathrm{u}>\mathrm{1}\:\mathrm{or}\:\mathrm{u}<−\mathrm{2} \\ $$$$\mathrm{But},\:\mathrm{u}\geqslant\mathrm{0}\Rightarrow\mathrm{u}<−\mathrm{2}\:\mathrm{is}\:\mathrm{not}\:\mathrm{possible}. \\ $$$$\therefore\:\mathrm{u}>\mathrm{1}\Rightarrow\sqrt{\mathrm{x}−\mathrm{4}}>\mathrm{1}\Rightarrow\mathrm{x}−\mathrm{4}>\mathrm{1}\Rightarrow\mathrm{x}>\mathrm{5} \\ $$
Commented by sou1618 last updated on 04/Oct/16
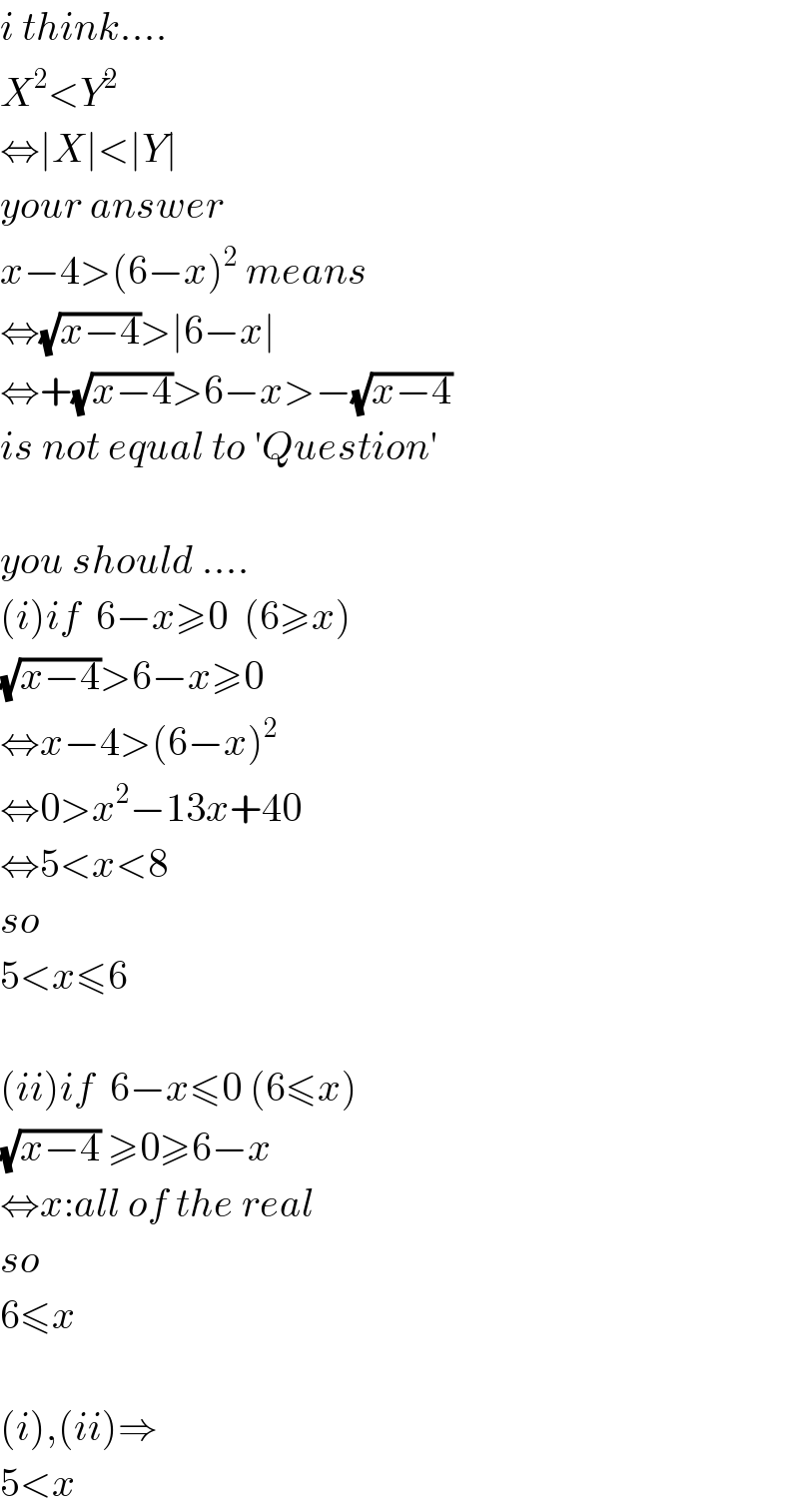
i think.... X^2 <Y^2 ⇔∣X∣<∣Y∣ your answer x−4>(6−x)^2 means ⇔(√(x−4))>∣6−x∣ ⇔+(√(x−4))>6−x>−(√(x−4)) is not equal to ′Question′ you should .... (i)if 6−x≥0 (6≥x) (√(x−4))>6−x≥0 ⇔x−4>(6−x)^2 ⇔0>x^2 −13x+40 ⇔5<x<8 so 5<x≤6 (ii)if 6−x≤0 (6≤x) (√(x−4)) ≥0≥6−x ⇔x:all of the real so 6≤x (i),(ii)⇒ 5<x
$${i}\:{think}…. \\ $$$${X}^{\mathrm{2}} <{Y}^{\mathrm{2}} \\ $$$$\Leftrightarrow\mid{X}\mid<\mid{Y}\mid \\ $$$${your}\:{answer} \\ $$$${x}−\mathrm{4}>\left(\mathrm{6}−{x}\right)^{\mathrm{2}} \:{means} \\ $$$$\Leftrightarrow\sqrt{{x}−\mathrm{4}}>\mid\mathrm{6}−{x}\mid \\ $$$$\Leftrightarrow+\sqrt{{x}−\mathrm{4}}>\mathrm{6}−{x}>−\sqrt{{x}−\mathrm{4}} \\ $$$${is}\:{not}\:{equal}\:{to}\:'{Question}' \\ $$$$ \\ $$$${you}\:{should}\:…. \\ $$$$\left({i}\right){if}\:\:\mathrm{6}−{x}\geqslant\mathrm{0}\:\:\left(\mathrm{6}\geqslant{x}\right) \\ $$$$\sqrt{{x}−\mathrm{4}}>\mathrm{6}−{x}\geqslant\mathrm{0} \\ $$$$\Leftrightarrow{x}−\mathrm{4}>\left(\mathrm{6}−{x}\right)^{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{0}>{x}^{\mathrm{2}} −\mathrm{13}{x}+\mathrm{40} \\ $$$$\Leftrightarrow\mathrm{5}<{x}<\mathrm{8} \\ $$$${so} \\ $$$$\mathrm{5}<{x}\leqslant\mathrm{6} \\ $$$$ \\ $$$$\left({ii}\right){if}\:\:\mathrm{6}−{x}\leqslant\mathrm{0}\:\left(\mathrm{6}\leqslant{x}\right) \\ $$$$\sqrt{{x}−\mathrm{4}}\:\geqslant\mathrm{0}\geqslant\mathrm{6}−{x} \\ $$$$\Leftrightarrow{x}:{all}\:{of}\:{the}\:{real} \\ $$$${so} \\ $$$$\mathrm{6}\leqslant{x} \\ $$$$ \\ $$$$\left({i}\right),\left({ii}\right)\Rightarrow \\ $$$$\mathrm{5}<{x} \\ $$
Commented by sandy_suhendra last updated on 04/Oct/16
thank′s for all of your answers, I really appreciate
$$\mathrm{thank}'\mathrm{s}\:\mathrm{for}\:\mathrm{all}\:\mathrm{of}\:\mathrm{your}\:\mathrm{answers},\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *