Question Number 787 by 123456 last updated on 22/Mar/15
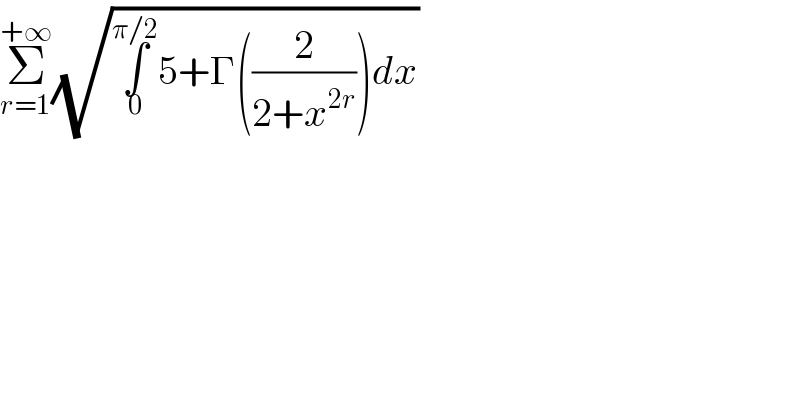
$$\underset{{r}=\mathrm{1}} {\overset{+\infty} {\sum}}\sqrt{\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\mathrm{5}+\Gamma\left(\frac{\mathrm{2}}{\mathrm{2}+{x}^{\mathrm{2}{r}} }\right){dx}} \\ $$
Commented by 123456 last updated on 13/Mar/15
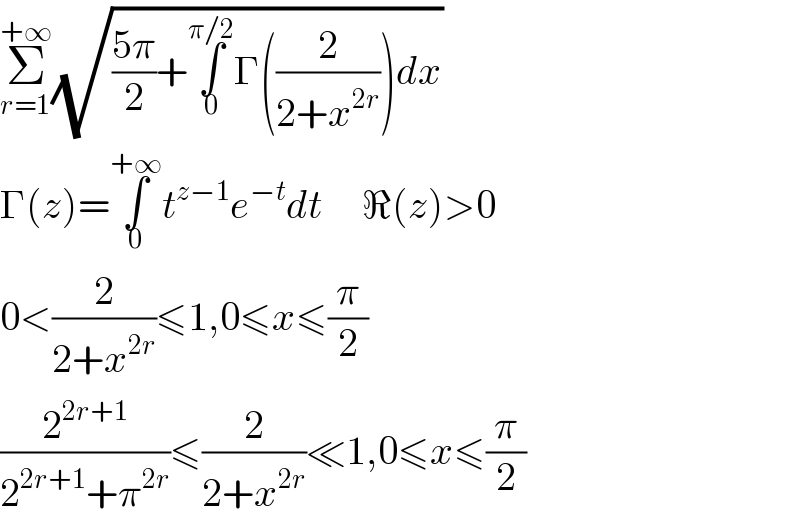
$$\underset{{r}=\mathrm{1}} {\overset{+\infty} {\sum}}\sqrt{\frac{\mathrm{5}\pi}{\mathrm{2}}+\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\Gamma\left(\frac{\mathrm{2}}{\mathrm{2}+{x}^{\mathrm{2}{r}} }\right){dx}} \\ $$$$\Gamma\left({z}\right)=\underset{\mathrm{0}} {\overset{+\infty} {\int}}{t}^{{z}−\mathrm{1}} {e}^{−{t}} {dt}\:\:\:\:\:\Re\left({z}\right)>\mathrm{0} \\ $$$$\mathrm{0}<\frac{\mathrm{2}}{\mathrm{2}+{x}^{\mathrm{2}{r}} }\leqslant\mathrm{1},\mathrm{0}\leqslant{x}\leqslant\frac{\pi}{\mathrm{2}} \\ $$$$\frac{\mathrm{2}^{\mathrm{2}{r}+\mathrm{1}} }{\mathrm{2}^{\mathrm{2}{r}+\mathrm{1}} +\pi^{\mathrm{2}{r}} }\leqslant\frac{\mathrm{2}}{\mathrm{2}+{x}^{\mathrm{2}{r}} }\ll\mathrm{1},\mathrm{0}\leqslant{x}\leqslant\frac{\pi}{\mathrm{2}} \\ $$
