r-1-n-1-r2-r-

Question Number 3682 by Yozzii last updated on 19/Dec/15

\underset{r = 1}{\sum^{n}} \frac{1}{r 2^{r}} = ?

Commented by RasheedSindhi last updated on 19/Dec/15

\underset{r = 1}{\sum^{n}} \frac{1}{r 2^{r}} = ?

\frac{1}{1 . 2^{1}} + \frac{1}{2 . 2^{2}} + \frac{1}{3 . 2^{3}} + \frac{1}{4 . 2^{4}} + \dots + \frac{1}{n 2^{n}}

\frac{A}{r} + \frac{B}{2^{r}} = \frac{1}{r 2^{r}}

A (2^{r}) + B (r) = 1

L e t r = 0

A (1) = 1 \Rightarrow A = 1

B (r) = 1 - 2^{r}

B = \frac{1 - 2^{r}}{r}

\frac{1}{r 2^{r}} = \frac{1}{r} + \frac{\frac{1 - 2^{r}}{r}}{2^{r}}

\underset{r = 1}{\sum^{n}} \frac{1}{r 2^{r}} = \underset{r = 1}{\sum^{n}} \frac{1}{r} + \underset{r = 1}{\sum^{n}} \frac{\frac{1 - 2^{r}}{r}}{2^{r}}

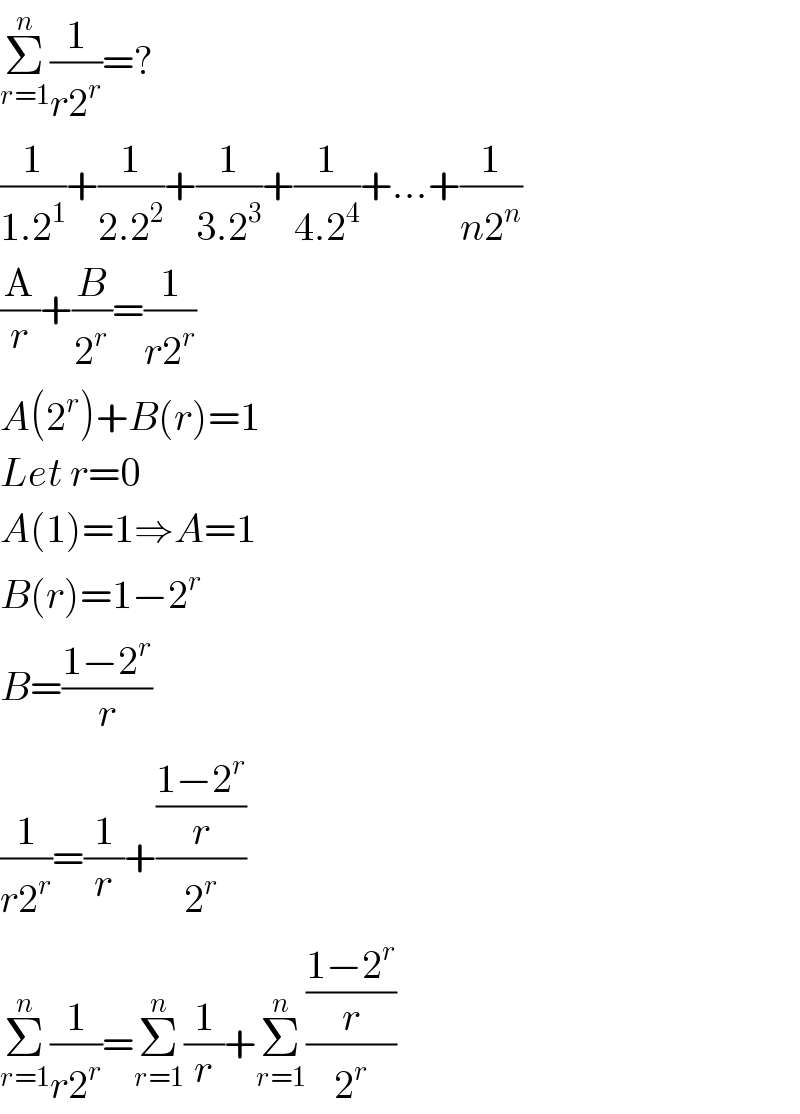
Commented by Yozzii last updated on 19/Dec/15

y = q^{- r - 1} \Rightarrow \int_{1}^{2} q^{- r - 1} d q = \frac{1}{- {r q}^{r}} ∣_{1}^{2}

\Rightarrow \underset{r = 1}{\sum^{n}} {\int_{1}^{2} {(q^{- 1})}^{r + 1} d q} = - \underset{r = 1}{\sum^{n}} (\frac{1}{r 2^{r}} - \frac{1}{r})

\underset{r = 1}{\sum^{n}} \frac{1}{{r q}^{r}} = \underset{r = 1}{\sum^{n}} \frac{1}{r} + \int_{1}^{2} {(q^{- 1})}^{2} \underset{r = 1}{\sum^{n}} {(q^{- 1})}^{r - 1} d \overset{}{q}

\underset{r = 1}{\sum^{n}} \frac{1}{{r q}^{r}} = \underset{r = 1}{\sum^{n}} \frac{1}{r} + {\int_{1}}^{2} {(q^{- 1})}^{2} \frac{(q^{- n} - 1)}{q^{- 1} - 1} d q

S (n) = H (n) + \int_{1}^{2} {(q^{- 1})}^{2} \frac{1 - q^{n}}{q^{n} (1 - q) / q} d q

S (n) - H (n) = \int_{1}^{2} \frac{1 - q^{n}}{q^{n + 1} (1 - q)} d q

Commented by Rasheed Soomro last updated on 19/Dec/15

\frac{1}{r 2^{r}} = \frac{A}{r} + \frac{B_{1}}{2} + \frac{B_{2}}{2^{2}} + \frac{B_{3}}{2^{3}} + \dots + \frac{B_{r}}{2^{r}}

A (2^{r}) + B_{1} (r 2^{r - 1}) + B_{2} (r 2^{r - 2}) + B_{3} (r 2^{r - 3}) + \dots + B_{r} (r) = 1

A c a n b e d e t e r m i n e d b y r = 0

B_{1}, B_{2}, \dots B_{r} = ? ? ?

H o w c a n w e d e t e r m i n e p a r t i a l f r a c t i o n s o f \frac{1}{r 2^{r}} ?

Commented by 123456 last updated on 19/Dec/15

i think it cant be made

or the coeficients A, B \dots

doenst be constant

Commented by prakash jain last updated on 19/Dec/15

S (n) = H (n) + . . has may have mistake somewhere

\lim_{n \to \infty} S (n) = \underset{r = 1}{\sum^{\infty}} \frac{1}{r \cdot 2^{r}} = \ln (2)

Commented by prakash jain last updated on 19/Dec/15

\underset{i = 2}{\sum^{\infty}} \frac{1}{x^{i}} = \frac{1 / x^{2}}{1 - 1 / x}, ∣ x ∣> 1

integrate

- \underset{i = 2}{\sum^{\infty}} \frac{1}{(i - 1) x^{i - 1}} = \int \frac{1}{x (x - 1)} = \ln (x - 1) - \ln x

\underset{i = 1}{\sum^{\infty}} \frac{1}{(i) x^{i}} = \int \frac{1}{x (x - 1)} = - \ln (x - 1) + \ln x

x = 2

\underset{i = 1}{\sum^{\infty}} \frac{1}{i 2^{i}} = \ln 2