Menu Close

R-e-its-s-3-ds-

Tinku Tara 0 Comments
Pin




Question Number 143190 by Ar Brandon last updated on 11/Jun/21
∫_R (e^(its) /(s+3))ds
$$\int_{\mathbb{R}} \frac{\mathrm{e}^{\mathrm{its}} }{\mathrm{s}+\mathrm{3}}\mathrm{ds} \\ $$
Commented by mohammad17 last updated on 11/Jun/21
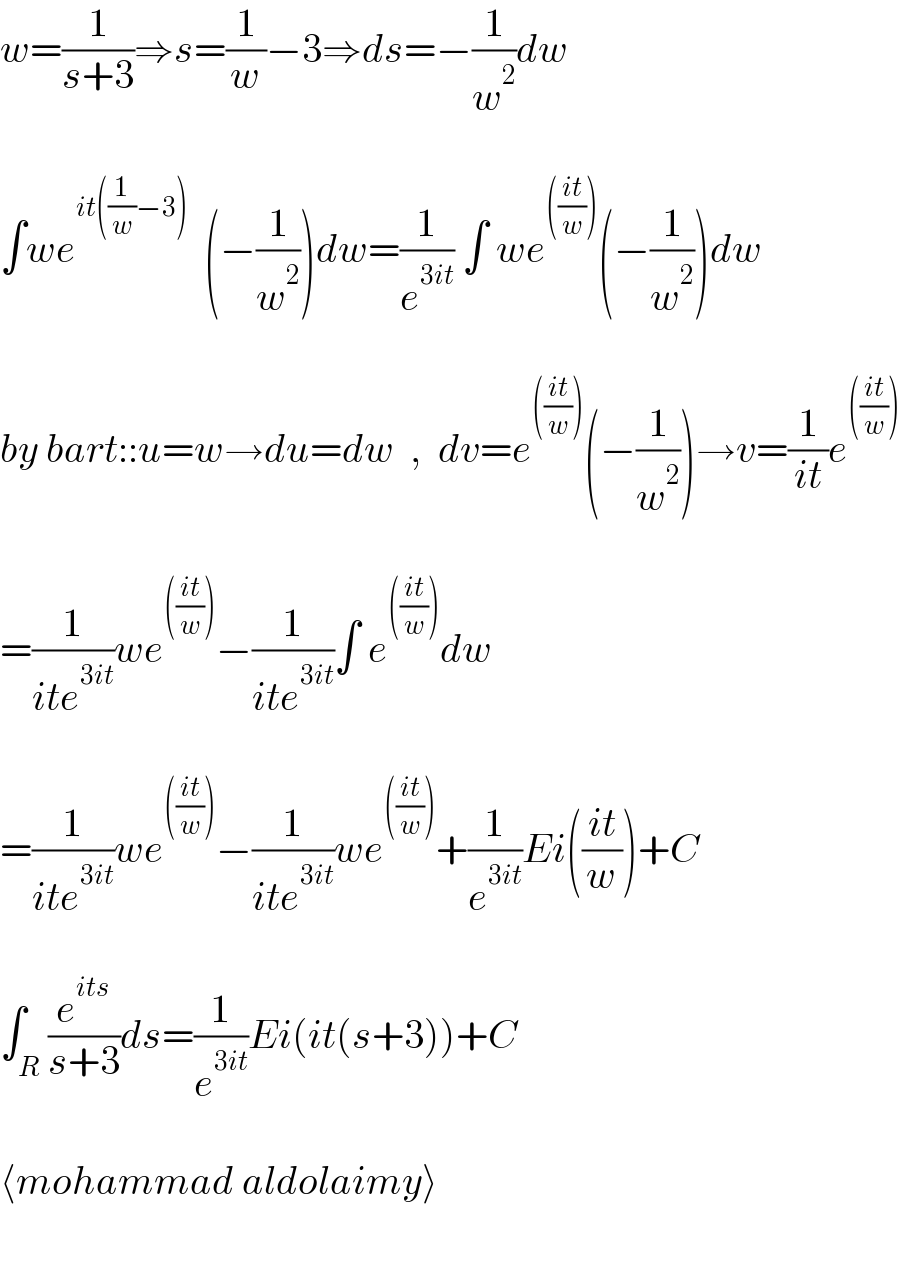
w=(1/(s+3))⇒s=(1/w)−3⇒ds=−(1/w^2 )dw ∫we^(it((1/w)−3)) (−(1/w^2 ))dw=(1/e^(3it) ) ∫ we^((((it)/w))) (−(1/w^2 ))dw by bart::u=w→du=dw , dv=e^((((it)/w))) (−(1/w^2 ))→v=(1/(it))e^((((it)/w))) =(1/(ite^(3it) ))we^((((it)/w))) −(1/(ite^(3it) ))∫ e^((((it)/w))) dw =(1/(ite^(3it) ))we^((((it)/w))) −(1/(ite^(3it) ))we^((((it)/w))) +(1/e^(3it) )Ei(((it)/w))+C ∫_R (e^(its) /(s+3))ds=(1/e^(3it) )Ei(it(s+3))+C ⟨mohammad aldolaimy⟩
$${w}=\frac{\mathrm{1}}{{s}+\mathrm{3}}\Rightarrow{s}=\frac{\mathrm{1}}{{w}}−\mathrm{3}\Rightarrow{ds}=−\frac{\mathrm{1}}{{w}^{\mathrm{2}} }{dw} \\ $$$$ \\ $$$$\int{we}^{{it}\left(\frac{\mathrm{1}}{{w}}−\mathrm{3}\right)} \:\:\left(−\frac{\mathrm{1}}{{w}^{\mathrm{2}} }\right){dw}=\frac{\mathrm{1}}{{e}^{\mathrm{3}{it}} }\:\int\:{we}^{\left(\frac{{it}}{{w}}\right)} \left(−\frac{\mathrm{1}}{{w}^{\mathrm{2}} }\right){dw} \\ $$$$ \\ $$$${by}\:{bart}::{u}={w}\rightarrow{du}={dw}\:\:,\:\:{dv}={e}^{\left(\frac{{it}}{{w}}\right)} \left(−\frac{\mathrm{1}}{{w}^{\mathrm{2}} }\right)\rightarrow{v}=\frac{\mathrm{1}}{{it}}{e}^{\left(\frac{{it}}{{w}}\right)} \\ $$$$ \\ $$$$=\frac{\mathrm{1}}{{ite}^{\mathrm{3}{it}} }{we}^{\left(\frac{{it}}{{w}}\right)} −\frac{\mathrm{1}}{{ite}^{\mathrm{3}{it}} }\int\:{e}^{\left(\frac{{it}}{{w}}\right)} {dw} \\ $$$$ \\ $$$$=\frac{\mathrm{1}}{{ite}^{\mathrm{3}{it}} }{we}^{\left(\frac{{it}}{{w}}\right)} −\frac{\mathrm{1}}{{ite}^{\mathrm{3}{it}} }{we}^{\left(\frac{{it}}{{w}}\right)} +\frac{\mathrm{1}}{{e}^{\mathrm{3}{it}} }{Ei}\left(\frac{{it}}{{w}}\right)+{C} \\ $$$$ \\ $$$$\int_{{R}} \frac{{e}^{{its}} }{{s}+\mathrm{3}}{ds}=\frac{\mathrm{1}}{{e}^{\mathrm{3}{it}} }{Ei}\left({it}\left({s}+\mathrm{3}\right)\right)+{C} \\ $$$$ \\ $$$$\langle{mohammad}\:{aldolaimy}\rangle \\ $$$$\: \\ $$
Commented by Ar Brandon last updated on 11/Jun/21
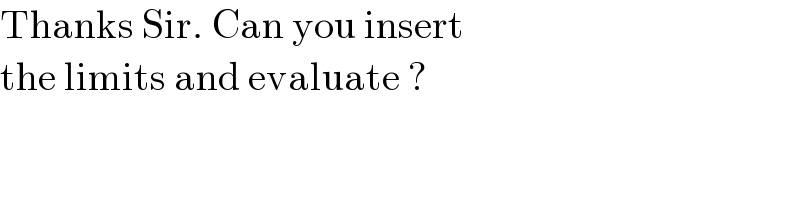
Thanks Sir. Can you insert the limits and evaluate ?
$$\mathrm{Thanks}\:\mathrm{Sir}.\:\mathrm{Can}\:\mathrm{you}\:\mathrm{insert}\: \\ $$$$\mathrm{the}\:\mathrm{limits}\:\mathrm{and}\:\mathrm{evaluate}\:? \\ $$
Answered by mathmax by abdo last updated on 11/Jun/21
Φ=∫_(−∞) ^(+∞) (e^(itx) /(x+3))dx =∫_(−∞) ^0 (e^(itx) /(x+3))dx +∫_0 ^∞ (e^(itx) /(x+3))dx but ∫_(−∞) ^0 (e^(itx) /(x+3))dx =_(x=−u) ∫_0 ^∞ (e^(−itu) /(3−u))du =∫_0 ^∞ (e^(−itx) /(3−x))dx ⇒ Φ=∫_0 ^∞ (e^(itx) /(x+3))dx +∫_0 ^∞ (e^(−itx) /(3−x))dx [we have ∫_0 ^∞ (e^(itx) /(x+3))dx =∫_0 ^∞ (∫_0 ^∞ e^(−(x+3)z) dz)e^(itx) dx =∫_0 ^∞ (∫_0 ^∞ e^((−z+it)x) dx)e^(−3z) dz =∫_0 ^∞ ([(1/(−z+it))e^((−z+it)x) ]_0 ^∞ )e^(−3z) dz =∫_0 ^∞ ((1/(−z+it)))e^(−3z) dz =−∫_0 ^∞ ((1/(z−it)))e^(−3z) dz =−∫_0 ^∞ (((z+it)e^(−3z) )/(z^2 +t^2 ))dz ∫_0 ^∞ (e^(−itx) /(3−x))dx =∫_0 ^∞ (∫_0 ^∞ e^(−(3−x)z) dz)e^(−itx) dx =∫_0 ^∞ (∫_0 ^∞ e^((z−it)x) dx)e^(−3z) dz =∫_0 ^∞ ([(1/(z−it))e^((z−it)x) ]_0 ^∞ )e^(−3z) dz =∫_0 ^∞ (−(1/(z−it)))e^(−3z) dz =−∫_0 ^∞ (((z+it)e^(−3z) )/(z^2 +t^2 ))dz ⇒ Φ=−∫_0 ^∞ (((z+it)e^(−3z) )/(z^2 +t^2 ))dz−∫_0 ^∞ (((z+it)e^(−3z) )/(z^2 +t^2 ))dz =−2∫_0 ^∞ (((z+it)e^(−3z) )/(z^2 +t^2 ))dz ....be continued....
$$\Phi=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{e}^{\mathrm{itx}} }{\mathrm{x}+\mathrm{3}}\mathrm{dx}\:=\int_{−\infty} ^{\mathrm{0}} \:\frac{\mathrm{e}^{\mathrm{itx}} }{\mathrm{x}+\mathrm{3}}\mathrm{dx}\:+\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{\mathrm{itx}} }{\mathrm{x}+\mathrm{3}}\mathrm{dx}\:\:\mathrm{but} \\ $$$$\int_{−\infty} ^{\mathrm{0}} \:\:\:\frac{\mathrm{e}^{\mathrm{itx}} }{\mathrm{x}+\mathrm{3}}\mathrm{dx}\:=_{\mathrm{x}=−\mathrm{u}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{itu}} }{\mathrm{3}−\mathrm{u}}\mathrm{du}\:\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{itx}} }{\mathrm{3}−\mathrm{x}}\mathrm{dx}\:\Rightarrow \\ $$$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{\mathrm{itx}} }{\mathrm{x}+\mathrm{3}}\mathrm{dx}\:+\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{itx}} }{\mathrm{3}−\mathrm{x}}\mathrm{dx}\:\left[\mathrm{we}\:\mathrm{have}\right. \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{\mathrm{itx}} }{\mathrm{x}+\mathrm{3}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\infty} \left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{x}+\mathrm{3}\right)\mathrm{z}} \mathrm{dz}\right)\mathrm{e}^{\mathrm{itx}} \mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{\left(−\mathrm{z}+\mathrm{it}\right)\mathrm{x}} \mathrm{dx}\right)\mathrm{e}^{−\mathrm{3z}} \mathrm{dz} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\left[\frac{\mathrm{1}}{−\mathrm{z}+\mathrm{it}}\mathrm{e}^{\left(−\mathrm{z}+\mathrm{it}\right)\mathrm{x}} \right]_{\mathrm{0}} ^{\infty} \right)\mathrm{e}^{−\mathrm{3z}} \mathrm{dz}\:=\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{−\mathrm{z}+\mathrm{it}}\right)\mathrm{e}^{−\mathrm{3z}} \mathrm{dz} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{z}−\mathrm{it}}\right)\mathrm{e}^{−\mathrm{3z}} \mathrm{dz}\:=−\int_{\mathrm{0}} ^{\infty} \:\frac{\left(\mathrm{z}+\mathrm{it}\right)\mathrm{e}^{−\mathrm{3z}} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{t}^{\mathrm{2}} }\mathrm{dz} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{itx}} }{\mathrm{3}−\mathrm{x}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\infty} \left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{3}−\mathrm{x}\right)\mathrm{z}} \mathrm{dz}\right)\mathrm{e}^{−\mathrm{itx}} \mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\left(\mathrm{z}−\mathrm{it}\right)\mathrm{x}} \mathrm{dx}\right)\mathrm{e}^{−\mathrm{3z}} \mathrm{dz} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\left[\frac{\mathrm{1}}{\mathrm{z}−\mathrm{it}}\mathrm{e}^{\left(\mathrm{z}−\mathrm{it}\right)\mathrm{x}} \right]_{\mathrm{0}} ^{\infty} \right)\mathrm{e}^{−\mathrm{3z}} \mathrm{dz} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(−\frac{\mathrm{1}}{\mathrm{z}−\mathrm{it}}\right)\mathrm{e}^{−\mathrm{3z}} \mathrm{dz}\:=−\int_{\mathrm{0}} ^{\infty} \frac{\left(\mathrm{z}+\mathrm{it}\right)\mathrm{e}^{−\mathrm{3z}} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{t}^{\mathrm{2}} }\mathrm{dz}\:\Rightarrow \\ $$$$\Phi=−\int_{\mathrm{0}} ^{\infty} \frac{\left(\mathrm{z}+\mathrm{it}\right)\mathrm{e}^{−\mathrm{3z}} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{t}^{\mathrm{2}} }\mathrm{dz}−\int_{\mathrm{0}} ^{\infty} \:\frac{\left(\mathrm{z}+\mathrm{it}\right)\mathrm{e}^{−\mathrm{3z}} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{t}^{\mathrm{2}} }\mathrm{dz} \\ $$$$=−\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\frac{\left(\mathrm{z}+\mathrm{it}\right)\mathrm{e}^{−\mathrm{3z}} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{t}^{\mathrm{2}} }\mathrm{dz}\:….\mathrm{be}\:\mathrm{continued}…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *