Menu Close

R-gt-0-0-lt-lt-f-m-sin-t-dt-f-r-sin-2-t-dt-f-m-pi-6-5pi-6-f-m-pi-6-pi-2-f-r-pi-6-5pi-6-f-r-pi-6-pi-

Tinku Tara 0 Comments
Pin




Question Number 1673 by 123456 last updated on 31/Aug/15
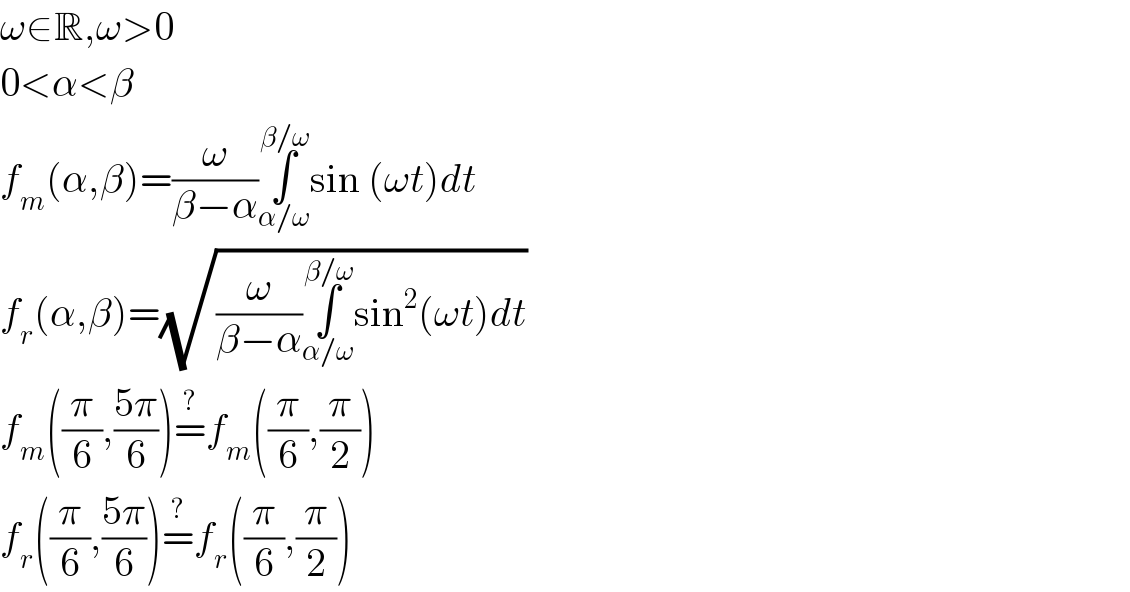
ω∈R,ω>0 0<α<β f_m (α,β)=(ω/(β−α))∫_(α/ω) ^(β/ω) sin (ωt)dt f_r (α,β)=(√((ω/(β−α))∫_(α/ω) ^(β/ω) sin^2 (ωt)dt)) f_m ((π/6),((5π)/6))=^? f_m ((π/6),(π/2)) f_r ((π/6),((5π)/6))=^? f_r ((π/6),(π/2))
$$\omega\in\mathbb{R},\omega>\mathrm{0} \\ $$$$\mathrm{0}<\alpha<\beta \\ $$$${f}_{{m}} \left(\alpha,\beta\right)=\frac{\omega}{\beta−\alpha}\underset{\alpha/\omega} {\overset{\beta/\omega} {\int}}\mathrm{sin}\:\left(\omega{t}\right){dt} \\ $$$${f}_{{r}} \left(\alpha,\beta\right)=\sqrt{\frac{\omega}{\beta−\alpha}\underset{\alpha/\omega} {\overset{\beta/\omega} {\int}}\mathrm{sin}^{\mathrm{2}} \left(\omega{t}\right){dt}} \\ $$$${f}_{{m}} \left(\frac{\pi}{\mathrm{6}},\frac{\mathrm{5}\pi}{\mathrm{6}}\right)\overset{?} {=}{f}_{{m}} \left(\frac{\pi}{\mathrm{6}},\frac{\pi}{\mathrm{2}}\right) \\ $$$${f}_{{r}} \left(\frac{\pi}{\mathrm{6}},\frac{\mathrm{5}\pi}{\mathrm{6}}\right)\overset{?} {=}{f}_{{r}} \left(\frac{\pi}{\mathrm{6}},\frac{\pi}{\mathrm{2}}\right) \\ $$
Answered by Yozzian last updated on 31/Aug/15
Under the integral within the given expressions of f_m (α,β) and f_r (α,β) ω is constant. So we can integrate as usual with ω>0. ∫_(α/ω) ^(β/ω) sinωt dt=−(1/ω)cos(ωt)∣_(α/ω) ^(β/ω) rhs=((−1)/ω)(cosβ−cosα) ∴ f_m (α,β)=((cosα−cosβ)/(β−α)) When α=π/6 and β=5π/6 f_m ((π/6),((5π)/6))=((cos((π/6))−cos(((5π)/6)))/(π((5/6)−(1/6)))) =((((√3)/2)−(−((√3)/2)))/((2π)/3)) f_m ((π/6),((5π)/6))=((3(√3))/(2π)).................. (1) When α=(π/6) and β=(π/2) we obtain f_m ((π/6),(π/2))=((cos((π/6))−cos((π/2)))/(π((1/2)−(1/6)))) =(((√3)/2−0)/(π/3)) f_m ((π/6),(π/2))=((3(√3))/(2π)) ....................(2) Upon comparison of results (1) and (2), we see that they are equal in value. Hence,f_m ((π/6),((5π)/6))=f_m ((π/6),(π/2)) . The next integral also has ω constant with respect to the variable under integration t. ∴∫_(α/ω) ^(β/ω) sin^2 ωt dt=(1/2)∫_(α/w) ^(β/ω) (1−cos(2ωt))dt rhs=(1/2)(t−(1/(2ω))sin(2ωt))∣_(α/ω) ^(β/ω) rhs=(1/2)(((β−α)/ω)+(1/(2ω))(sin(2α)−sin(2β))) rhs=((2(β−α)+sin2α−sin2β)/(4ω)) ∴f_r (α,β)=(√((2(β−α)+sin2α−sin2β)/(4(β−α)))) When α=(π/6) and β=((5π)/6) we get f_r ((π/6),((5π)/6))=(√((1/2)+((sin(π/3)−sin((5π)/3))/((2π)/3)))) =(√((1/2)+((((√3)/2)−(−((√3)/2)))/(2π/3)))) =(√((1/2)+((3(√3))/(2π)))) f_r ((π/6),((5π)/6))=(√((π+3(√3))/(2π))). .......(3) When α=(π/6) and β=(π/2) we have f_r ((π/6),(π/2))=(√((1/2)+((sin(π/3)−sinπ)/(π/3)))) =(√((π+3(√3))/(2π))). ........(4) On comparing the results (3) and (4) we see that they are equal in value. Hence, f_r ((π/6),((5π)/6))=f_r ((π/6),(π/2)) .
$${Under}\:{the}\:{integral}\:{within}\:{the}\:{given} \\ $$$${expressions}\:{of}\:{f}_{{m}} \left(\alpha,\beta\right)\:{and}\:{f}_{{r}} \left(\alpha,\beta\right) \\ $$$$\omega\:{is}\:{constant}.\:{So}\:{we}\:{can}\:{integrate} \\ $$$${as}\:{usual}\:{with}\:\omega>\mathrm{0}. \\ $$$$\int_{\alpha/\omega} ^{\beta/\omega} {sin}\omega{t}\:{dt}=−\frac{\mathrm{1}}{\omega}{cos}\left(\omega{t}\right)\mid_{\alpha/\omega} ^{\beta/\omega} \\ $$$${rhs}=\frac{−\mathrm{1}}{\omega}\left({cos}\beta−{cos}\alpha\right) \\ $$$$\therefore\:{f}_{{m}} \left(\alpha,\beta\right)=\frac{{cos}\alpha−{cos}\beta}{\beta−\alpha} \\ $$$${When}\:\alpha=\pi/\mathrm{6}\:{and}\:\beta=\mathrm{5}\pi/\mathrm{6} \\ $$$${f}_{{m}} \left(\frac{\pi}{\mathrm{6}},\frac{\mathrm{5}\pi}{\mathrm{6}}\right)=\frac{{cos}\left(\frac{\pi}{\mathrm{6}}\right)−{cos}\left(\frac{\mathrm{5}\pi}{\mathrm{6}}\right)}{\pi\left(\frac{\mathrm{5}}{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{6}}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\left(−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)}{\frac{\mathrm{2}\pi}{\mathrm{3}}} \\ $$$${f}_{{m}} \left(\frac{\pi}{\mathrm{6}},\frac{\mathrm{5}\pi}{\mathrm{6}}\right)=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}\pi}………………\:\left(\mathrm{1}\right) \\ $$$${When}\:\alpha=\frac{\pi}{\mathrm{6}}\:{and}\:\beta=\frac{\pi}{\mathrm{2}}\:{we}\:{obtain} \\ $$$${f}_{{m}} \left(\frac{\pi}{\mathrm{6}},\frac{\pi}{\mathrm{2}}\right)=\frac{{cos}\left(\frac{\pi}{\mathrm{6}}\right)−{cos}\left(\frac{\pi}{\mathrm{2}}\right)}{\pi\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{6}}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{3}}/\mathrm{2}−\mathrm{0}}{\pi/\mathrm{3}} \\ $$$${f}_{{m}} \left(\frac{\pi}{\mathrm{6}},\frac{\pi}{\mathrm{2}}\right)=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}\pi}\:\:………………..\left(\mathrm{2}\right) \\ $$$${Upon}\:{comparison}\:{of}\:{results}\:\left(\mathrm{1}\right)\: \\ $$$${and}\:\left(\mathrm{2}\right),\:{we}\:{see}\:{that}\:{they}\:{are}\:{equal} \\ $$$${in}\:{value}.\: \\ $$$${Hence},{f}_{{m}} \left(\frac{\pi}{\mathrm{6}},\frac{\mathrm{5}\pi}{\mathrm{6}}\right)={f}_{{m}} \left(\frac{\pi}{\mathrm{6}},\frac{\pi}{\mathrm{2}}\right)\:. \\ $$$$ \\ $$$${The}\:{next}\:{integral}\:{also}\:{has}\:\omega\: \\ $$$${constant}\:{with}\:{respect}\:{to}\:{the}\: \\ $$$${variable}\:{under}\:{integration}\:{t}. \\ $$$$\therefore\int_{\alpha/\omega} ^{\beta/\omega} {sin}^{\mathrm{2}} \omega{t}\:{dt}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\alpha/{w}} ^{\beta/\omega} \left(\mathrm{1}−{cos}\left(\mathrm{2}\omega{t}\right)\right){dt} \\ $$$${rhs}=\frac{\mathrm{1}}{\mathrm{2}}\left({t}−\frac{\mathrm{1}}{\mathrm{2}\omega}{sin}\left(\mathrm{2}\omega{t}\right)\right)\mid_{\alpha/\omega} ^{\beta/\omega} \\ $$$${rhs}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\beta−\alpha}{\omega}+\frac{\mathrm{1}}{\mathrm{2}\omega}\left({sin}\left(\mathrm{2}\alpha\right)−{sin}\left(\mathrm{2}\beta\right)\right)\right) \\ $$$${rhs}=\frac{\mathrm{2}\left(\beta−\alpha\right)+{sin}\mathrm{2}\alpha−{sin}\mathrm{2}\beta}{\mathrm{4}\omega} \\ $$$$\therefore{f}_{{r}} \left(\alpha,\beta\right)=\sqrt{\frac{\mathrm{2}\left(\beta−\alpha\right)+{sin}\mathrm{2}\alpha−{sin}\mathrm{2}\beta}{\mathrm{4}\left(\beta−\alpha\right)}} \\ $$$${When}\:\alpha=\frac{\pi}{\mathrm{6}}\:{and}\:\beta=\frac{\mathrm{5}\pi}{\mathrm{6}}\:{we}\:{get} \\ $$$${f}_{{r}} \left(\frac{\pi}{\mathrm{6}},\frac{\mathrm{5}\pi}{\mathrm{6}}\right)=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{{sin}\frac{\pi}{\mathrm{3}}−{sin}\frac{\mathrm{5}\pi}{\mathrm{3}}}{\frac{\mathrm{2}\pi}{\mathrm{3}}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\left(−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)}{\mathrm{2}\pi/\mathrm{3}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}\pi}} \\ $$$${f}_{{r}} \left(\frac{\pi}{\mathrm{6}},\frac{\mathrm{5}\pi}{\mathrm{6}}\right)=\sqrt{\frac{\pi+\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}\pi}}.\:…….\left(\mathrm{3}\right) \\ $$$${When}\:\alpha=\frac{\pi}{\mathrm{6}}\:{and}\:\beta=\frac{\pi}{\mathrm{2}}\:{we}\:{have} \\ $$$${f}_{{r}} \left(\frac{\pi}{\mathrm{6}},\frac{\pi}{\mathrm{2}}\right)=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}+\frac{{sin}\frac{\pi}{\mathrm{3}}−{sin}\pi}{\pi/\mathrm{3}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\frac{\pi+\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}\pi}}.\:\:……..\left(\mathrm{4}\right) \\ $$$${On}\:{comparing}\:{the}\:{results}\:\left(\mathrm{3}\right)\:{and} \\ $$$$\left(\mathrm{4}\right)\:{we}\:{see}\:{that}\:{they}\:{are}\:{equal}\:{in} \\ $$$${value}.\:{Hence}, \\ $$$$\:\:\:\:\:\:\:\:\:\:{f}_{{r}} \left(\frac{\pi}{\mathrm{6}},\frac{\mathrm{5}\pi}{\mathrm{6}}\right)={f}_{{r}} \left(\frac{\pi}{\mathrm{6}},\frac{\pi}{\mathrm{2}}\right)\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *