Menu Close

reposting-this-x-4-1-2a-x-2-2ax-1-0-solve-for-a-gt-0-x-gt-0-a-5-23-8-x-4-49-4-x-3-27-8-x-2-3x-9-8-0-3-real-solutions-a-1-lt-a-2-lt-a-3-we-cannot-

Tinku Tara
Pin




Question Number 65569 by MJS last updated on 31/Jul/19
reposting this: x^4 +(1−2a)x^2 −2ax+1=0 solve for a>0∧x>0 a^5 −((23)/8)x^4 −((49)/4)x^3 +((27)/8)x^2 +3x+(9/8)=0 ⇒ 3 real solutions a_1 <a_2 <a_3 we cannot solve exactly (?) so it′s not possible to get all the below solutions exactly, only rough approximations for the following α,β,γ,δ ∈R the possible natures of the zeros: (1) a<a_1 ∨a_2 <a<a_3 ⇒ x=α∨x=β∨x=γ±δi (2) a>a_3 ⇒ x=α∨x=β∨x=γ∨x=δ (3) a_1 <a<a_2 ⇒ x=α±βi∨x=γ±δi (4) a=a_3 ⇒ x=α=β∨x=γ∨x=δ (5) a=a_1 ∨a=a_2 ⇒ x=α=β∨x=γ±δi
$$\mathrm{reposting}\:\mathrm{this}: \\ $$$${x}^{\mathrm{4}} +\left(\mathrm{1}−\mathrm{2}{a}\right){x}^{\mathrm{2}} −\mathrm{2}{ax}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{solve}\:\mathrm{for}\:{a}>\mathrm{0}\wedge{x}>\mathrm{0} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:{a}^{\mathrm{5}} −\frac{\mathrm{23}}{\mathrm{8}}{x}^{\mathrm{4}} −\frac{\mathrm{49}}{\mathrm{4}}{x}^{\mathrm{3}} +\frac{\mathrm{27}}{\mathrm{8}}{x}^{\mathrm{2}} +\mathrm{3}{x}+\frac{\mathrm{9}}{\mathrm{8}}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\mathrm{3}\:\mathrm{real}\:\mathrm{solutions}\:{a}_{\mathrm{1}} <{a}_{\mathrm{2}} <{a}_{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{we}\:\mathrm{cannot}\:\mathrm{solve}\:\mathrm{exactly}\:\left(?\right)\:\mathrm{so}\:\mathrm{it}'\mathrm{s}\:\mathrm{not} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{possible}\:\mathrm{to}\:\mathrm{get}\:\mathrm{all}\:\mathrm{the}\:\mathrm{below}\:\mathrm{solutions} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{exactly},\:\mathrm{only}\:\mathrm{rough}\:\mathrm{approximations} \\ $$$$ \\ $$$$\mathrm{for}\:\mathrm{the}\:\mathrm{following}\:\alpha,\beta,\gamma,\delta\:\in\mathbb{R} \\ $$$$\mathrm{the}\:\mathrm{possible}\:\mathrm{natures}\:\mathrm{of}\:\mathrm{the}\:\mathrm{zeros}: \\ $$$$\left(\mathrm{1}\right)\:\:{a}<{a}_{\mathrm{1}} \vee{a}_{\mathrm{2}} <{a}<{a}_{\mathrm{3}} \:\Rightarrow\:{x}=\alpha\vee{x}=\beta\vee{x}=\gamma\pm\delta\mathrm{i} \\ $$$$\left(\mathrm{2}\right)\:\:{a}>{a}_{\mathrm{3}} \:\Rightarrow\:{x}=\alpha\vee{x}=\beta\vee{x}=\gamma\vee{x}=\delta \\ $$$$\left(\mathrm{3}\right)\:\:{a}_{\mathrm{1}} <{a}<{a}_{\mathrm{2}} \:\Rightarrow\:{x}=\alpha\pm\beta\mathrm{i}\vee{x}=\gamma\pm\delta\mathrm{i} \\ $$$$\left(\mathrm{4}\right)\:\:{a}={a}_{\mathrm{3}} \:\Rightarrow\:{x}=\alpha=\beta\vee{x}=\gamma\vee{x}=\delta \\ $$$$\left(\mathrm{5}\right)\:\:{a}={a}_{\mathrm{1}} \vee{a}={a}_{\mathrm{2}} \:\Rightarrow\:{x}=\alpha=\beta\vee{x}=\gamma\pm\delta\mathrm{i} \\ $$
Commented by MJS last updated on 31/Jul/19
please someone check
$$\mathrm{please}\:\mathrm{someone}\:\mathrm{check} \\ $$
Answered by Prithwish sen last updated on 31/Jul/19
Commented by Prithwish sen last updated on 31/Jul/19
Commented by Prithwish sen last updated on 31/Jul/19
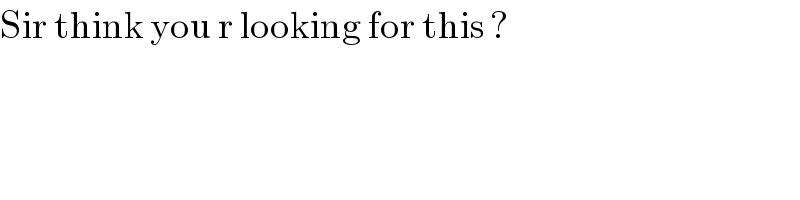
Sir think you r looking for this ?
$$\mathrm{Sir}\:\mathrm{think}\:\mathrm{you}\:\mathrm{r}\:\mathrm{looking}\:\mathrm{for}\:\mathrm{this}\:? \\ $$
Commented by MJS last updated on 31/Jul/19
yes thank you but I had made 2 typos. it must be q not r in two of the cases...
$$\mathrm{yes}\:\mathrm{thank}\:\mathrm{you} \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{had}\:\mathrm{made}\:\mathrm{2}\:\mathrm{typos}.\:\mathrm{it}\:\mathrm{must}\:\mathrm{be}\:{q}\:\mathrm{not}\:{r} \\ $$$$\mathrm{in}\:\mathrm{two}\:\mathrm{of}\:\mathrm{the}\:\mathrm{cases}… \\ $$
Commented by MJS last updated on 31/Jul/19
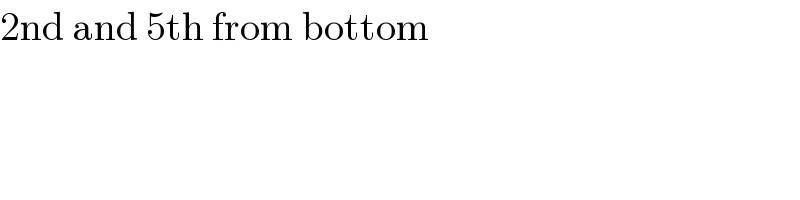
2nd and 5th from bottom
$$\mathrm{2nd}\:\mathrm{and}\:\mathrm{5th}\:\mathrm{from}\:\mathrm{bottom} \\ $$

Pin