Question Number 78314 by mfwajoel1 last updated on 15/Jan/20
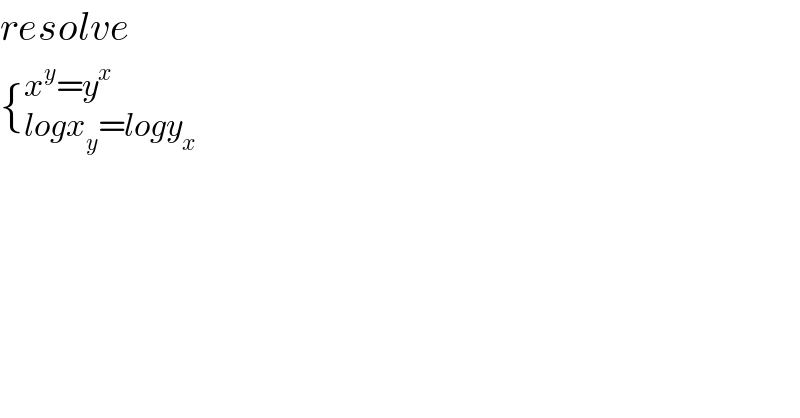
$${resolve} \\ $$$$\left\{_{{logx}_{{y}} ={logy}_{{x}} } ^{{x}^{{y}} ={y}^{{x}} } \right. \\ $$
Commented by john santu last updated on 16/Jan/20
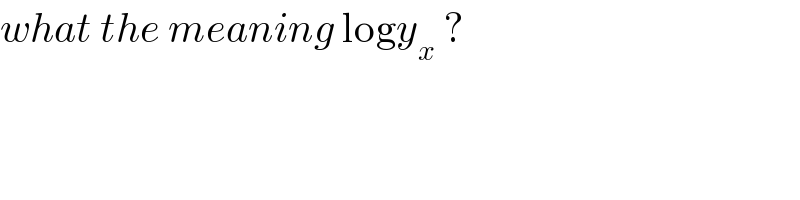
$${what}\:{the}\:{meaning}\:\mathrm{log}{y}_{{x}} \:? \\ $$
Answered by MJS last updated on 16/Jan/20
![if you mean log_y x =log_x y (1) ⇒ yln x =xln y (2) ⇒ ((ln x)/(ln y))=((ln y)/(ln x)) ⇒ ln y =±ln x ⇒ y=x∨y=(1/x) [(a/b)=(b/a) ⇒ a^2 =b^2 ⇒ b=±a] case 1 y=x ⇒ (1) x^x =x^x true for x∈C\{0} case 2 y=(1/x) ⇒ (1) ((ln x)/x)=xln (1/x) ((ln x)/x)=−xln x (1/x)=−x ⇒ x=±i ⇒ y=∓i](https://www.tinkutara.com/question/Q78339.png)
$$\mathrm{if}\:\mathrm{you}\:\mathrm{mean}\:\mathrm{log}_{{y}} \:{x}\:=\mathrm{log}_{{x}} \:{y} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\Rightarrow\:{y}\mathrm{ln}\:{x}\:={x}\mathrm{ln}\:{y} \\ $$$$\left(\mathrm{2}\right)\:\Rightarrow\:\frac{\mathrm{ln}\:{x}}{\mathrm{ln}\:{y}}=\frac{\mathrm{ln}\:{y}}{\mathrm{ln}\:{x}}\:\Rightarrow\:\mathrm{ln}\:{y}\:=\pm\mathrm{ln}\:{x}\:\Rightarrow\:{y}={x}\vee{y}=\frac{\mathrm{1}}{{x}} \\ $$$$\:\:\:\:\:\left[\frac{{a}}{{b}}=\frac{{b}}{{a}}\:\Rightarrow\:{a}^{\mathrm{2}} ={b}^{\mathrm{2}} \:\Rightarrow\:{b}=\pm{a}\right] \\ $$$$\mathrm{case}\:\mathrm{1}\:{y}={x} \\ $$$$\Rightarrow\:\left(\mathrm{1}\right)\:{x}^{{x}} ={x}^{{x}} \:\mathrm{true}\:\mathrm{for}\:{x}\in\mathbb{C}\backslash\left\{\mathrm{0}\right\} \\ $$$$\mathrm{case}\:\mathrm{2}\:{y}=\frac{\mathrm{1}}{{x}} \\ $$$$\Rightarrow\:\left(\mathrm{1}\right)\:\frac{\mathrm{ln}\:{x}}{{x}}={x}\mathrm{ln}\:\frac{\mathrm{1}}{{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{ln}\:{x}}{{x}}=−{x}\mathrm{ln}\:{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{{x}}=−{x}\:\Rightarrow\:{x}=\pm\mathrm{i}\:\Rightarrow\:{y}=\mp\mathrm{i} \\ $$
