Question Number 4285 by Filup last updated on 07/Jan/16

$${S}=\mathrm{1}+\sqrt{\mathrm{2}+\sqrt{\mathrm{3}+\sqrt{\mathrm{4}+…}}} \\ $$$${S}=??? \\ $$
Commented by RasheedSindhi last updated on 07/Jan/16
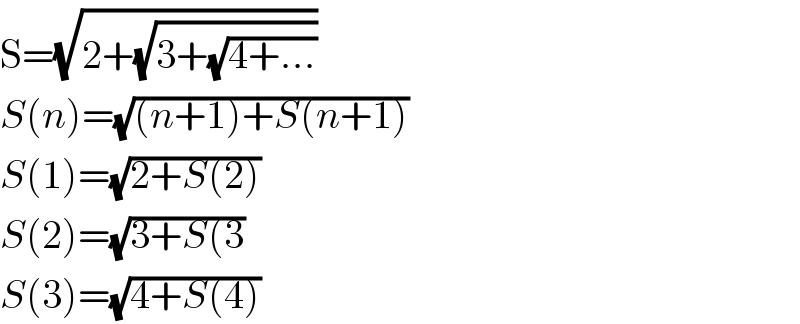
$$\mathrm{S}=\sqrt{\mathrm{2}+\sqrt{\mathrm{3}+\sqrt{\mathrm{4}+…}}} \\ $$$${S}\left({n}\right)=\sqrt{\left({n}+\mathrm{1}\right)+{S}\left({n}+\mathrm{1}\right)} \\ $$$${S}\left(\mathrm{1}\right)=\sqrt{\mathrm{2}+{S}\left(\mathrm{2}\right)} \\ $$$${S}\left(\mathrm{2}\right)=\sqrt{\mathrm{3}+{S}\left(\mathrm{3}\right.} \\ $$$${S}\left(\mathrm{3}\right)=\sqrt{\mathrm{4}+{S}\left(\mathrm{4}\right)} \\ $$
Commented by Rasheed Soomro last updated on 10/Jan/16
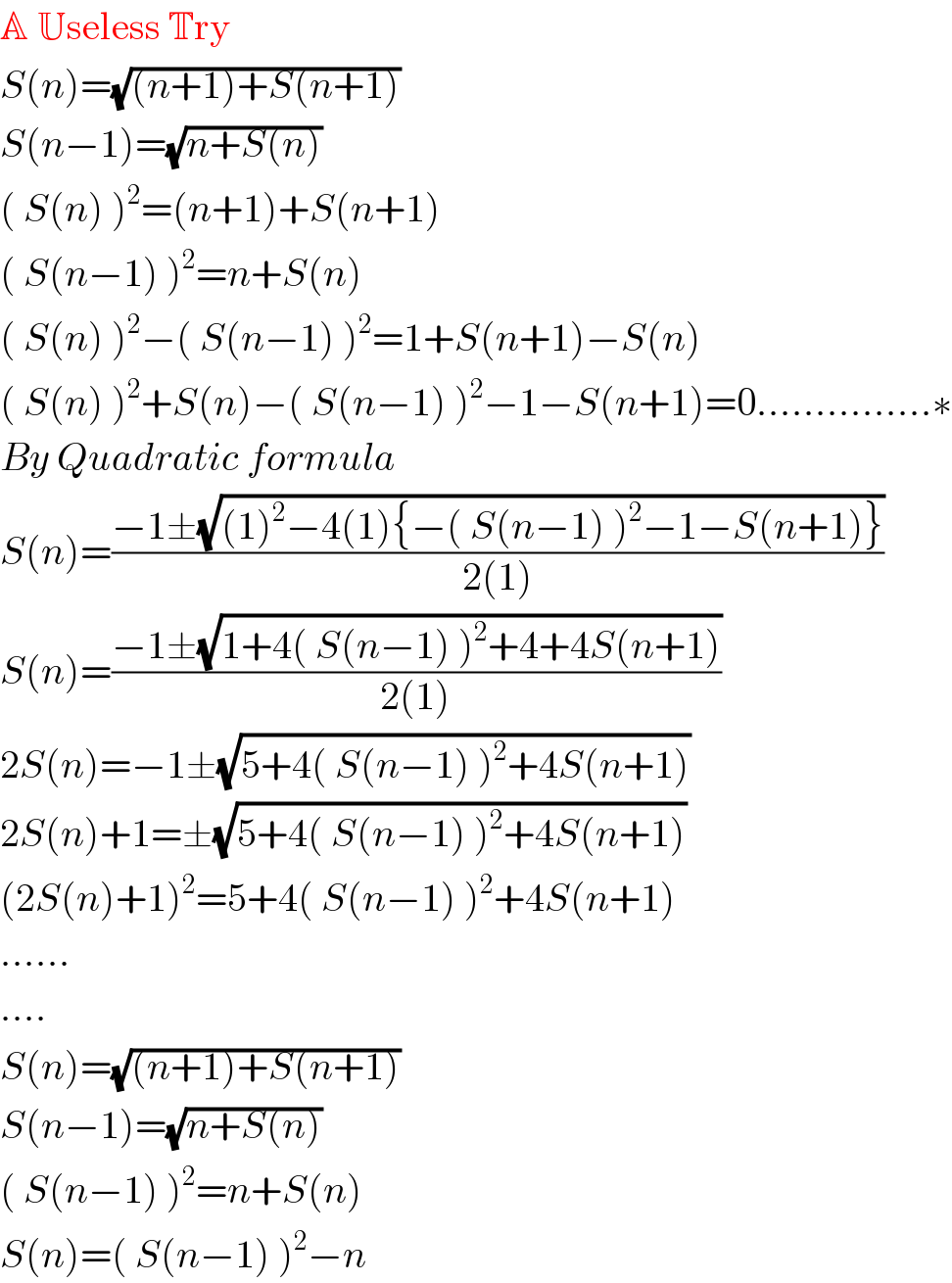
$$\mathbb{A}\:\mathbb{U}\mathrm{seless}\:\mathbb{T}\mathrm{ry} \\ $$$${S}\left({n}\right)=\sqrt{\left({n}+\mathrm{1}\right)+{S}\left({n}+\mathrm{1}\right)} \\ $$$${S}\left({n}−\mathrm{1}\right)=\sqrt{{n}+{S}\left({n}\right)} \\ $$$$\left(\:{S}\left({n}\right)\:\right)^{\mathrm{2}} =\left({n}+\mathrm{1}\right)+{S}\left({n}+\mathrm{1}\right) \\ $$$$\left(\:{S}\left({n}−\mathrm{1}\right)\:\right)^{\mathrm{2}} ={n}+{S}\left({n}\right) \\ $$$$\left(\:{S}\left({n}\right)\:\right)^{\mathrm{2}} −\left(\:{S}\left({n}−\mathrm{1}\right)\:\right)^{\mathrm{2}} =\mathrm{1}+{S}\left({n}+\mathrm{1}\right)−{S}\left({n}\right) \\ $$$$\left(\:{S}\left({n}\right)\:\right)^{\mathrm{2}} +{S}\left({n}\right)−\left(\:{S}\left({n}−\mathrm{1}\right)\:\right)^{\mathrm{2}} −\mathrm{1}−{S}\left({n}+\mathrm{1}\right)=\mathrm{0}……………\ast \\ $$$${By}\:{Quadratic}\:{formula} \\ $$$${S}\left({n}\right)=\frac{−\mathrm{1}\pm\sqrt{\left(\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}\right)\left\{−\left(\:{S}\left({n}−\mathrm{1}\right)\:\right)^{\mathrm{2}} −\mathrm{1}−{S}\left({n}+\mathrm{1}\right)\right\}}}{\mathrm{2}\left(\mathrm{1}\right)} \\ $$$${S}\left({n}\right)=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{4}\left(\:{S}\left({n}−\mathrm{1}\right)\:\right)^{\mathrm{2}} +\mathrm{4}+\mathrm{4}{S}\left({n}+\mathrm{1}\right)}}{\mathrm{2}\left(\mathrm{1}\right)} \\ $$$$\mathrm{2}{S}\left({n}\right)=−\mathrm{1}\pm\sqrt{\mathrm{5}+\mathrm{4}\left(\:{S}\left({n}−\mathrm{1}\right)\:\right)^{\mathrm{2}} +\mathrm{4}{S}\left({n}+\mathrm{1}\right)} \\ $$$$\mathrm{2}{S}\left({n}\right)+\mathrm{1}=\pm\sqrt{\mathrm{5}+\mathrm{4}\left(\:{S}\left({n}−\mathrm{1}\right)\:\right)^{\mathrm{2}} +\mathrm{4}{S}\left({n}+\mathrm{1}\right)} \\ $$$$\left(\mathrm{2}{S}\left({n}\right)+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{5}+\mathrm{4}\left(\:{S}\left({n}−\mathrm{1}\right)\:\right)^{\mathrm{2}} +\mathrm{4}{S}\left({n}+\mathrm{1}\right) \\ $$$$…… \\ $$$$…. \\ $$$${S}\left({n}\right)=\sqrt{\left({n}+\mathrm{1}\right)+{S}\left({n}+\mathrm{1}\right)} \\ $$$${S}\left({n}−\mathrm{1}\right)=\sqrt{{n}+{S}\left({n}\right)} \\ $$$$\left(\:{S}\left({n}−\mathrm{1}\right)\:\right)^{\mathrm{2}} ={n}+{S}\left({n}\right) \\ $$$${S}\left({n}\right)=\left(\:{S}\left({n}−\mathrm{1}\right)\:\right)^{\mathrm{2}} −{n} \\ $$
Commented by Rasheed Soomro last updated on 13/Jan/16
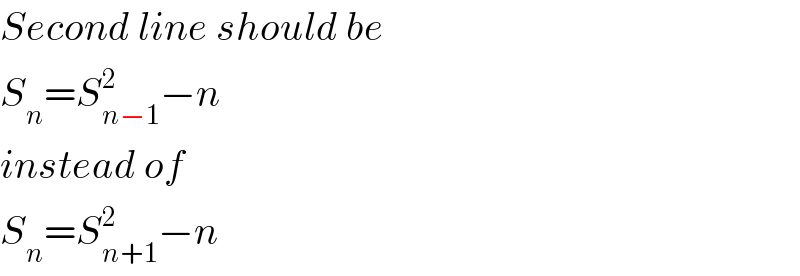
$${Second}\:{line}\:{should}\:{be} \\ $$$${S}_{{n}} ={S}_{{n}−\mathrm{1}} ^{\mathrm{2}} −{n} \\ $$$${instead}\:{of}\: \\ $$$${S}_{{n}} ={S}_{{n}+\mathrm{1}} ^{\mathrm{2}} −{n} \\ $$
Commented by Filup last updated on 13/Jan/16
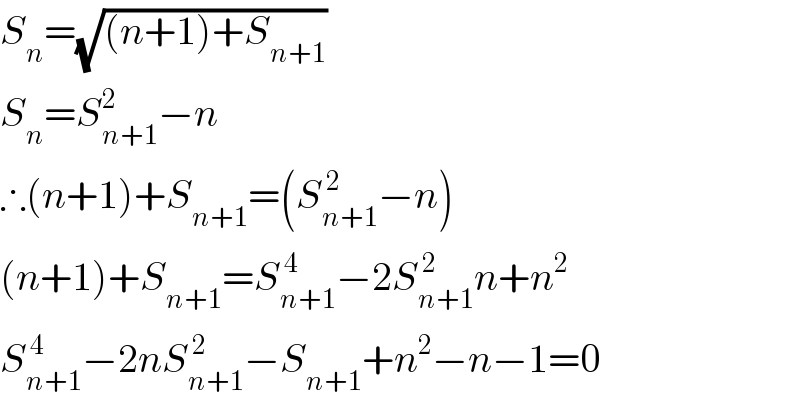
$${S}_{{n}} =\sqrt{\left({n}+\mathrm{1}\right)+{S}_{{n}+\mathrm{1}} } \\ $$$${S}_{{n}} ={S}_{{n}+\mathrm{1}} ^{\mathrm{2}} −{n} \\ $$$$\therefore\left({n}+\mathrm{1}\right)+{S}_{{n}+\mathrm{1}} =\left({S}_{{n}+\mathrm{1}} ^{\:\mathrm{2}} −{n}\right) \\ $$$$\left({n}+\mathrm{1}\right)+{S}_{{n}+\mathrm{1}} ={S}_{{n}+\mathrm{1}} ^{\:\mathrm{4}} −\mathrm{2}{S}_{{n}+\mathrm{1}} ^{\:\mathrm{2}} {n}+{n}^{\mathrm{2}} \\ $$$${S}_{{n}+\mathrm{1}} ^{\:\mathrm{4}} −\mathrm{2}{nS}_{{n}+\mathrm{1}} ^{\:\mathrm{2}} −{S}_{{n}+\mathrm{1}} +{n}^{\mathrm{2}} −{n}−\mathrm{1}=\mathrm{0} \\ $$
Commented by Filup last updated on 11/Jan/16
![S(n)=[S(n−1)]^2 −n or S_n =S_(n−1) ^( 2) −n What is the limit as n→∞?](https://www.tinkutara.com/question/Q4345.png)
$${S}\left({n}\right)=\left[{S}\left({n}−\mathrm{1}\right)\right]^{\mathrm{2}} −{n} \\ $$$${or} \\ $$$${S}_{{n}} ={S}_{{n}−\mathrm{1}} ^{\:\mathrm{2}} −{n} \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{limit}\:\mathrm{as}\:{n}\rightarrow\infty? \\ $$
Commented by Rasheed Soomro last updated on 11/Jan/16

$$\mathrm{I}\:\mathrm{thought}\:\mathrm{for}\:\mathrm{that}\:\mathrm{but}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{how} \\ $$$$\mathrm{to}\:\mathrm{determine}\:\mathrm{it}. \\ $$
