Question Number 7999 by FilupSmith last updated on 27/Sep/16
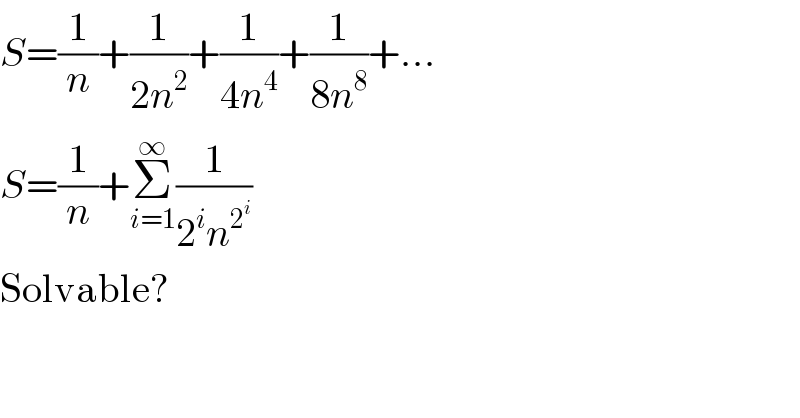
$${S}=\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{8}{n}^{\mathrm{8}} }+… \\ $$$${S}=\frac{\mathrm{1}}{{n}}+\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{i}} {n}^{\mathrm{2}^{{i}} } } \\ $$$$\mathrm{Solvable}? \\ $$
Answered by Yozzia last updated on 27/Sep/16
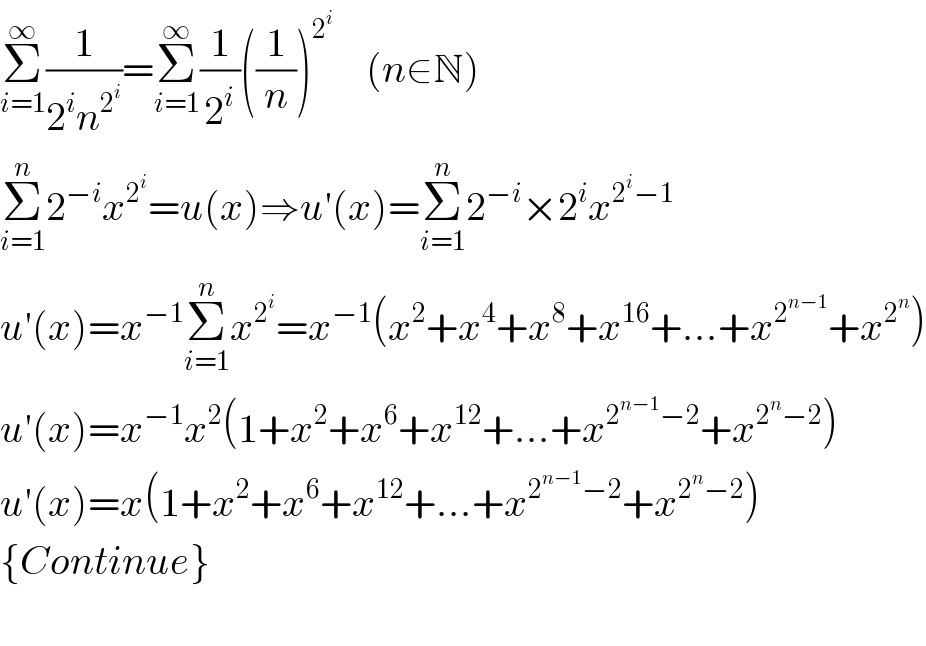
$$\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{i}} {n}^{\mathrm{2}^{{i}} } }=\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{i}} }\left(\frac{\mathrm{1}}{{n}}\right)^{\mathrm{2}^{{i}} } \:\:\:\:\left({n}\in\mathbb{N}\right) \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{2}^{−{i}} {x}^{\mathrm{2}^{{i}} } ={u}\left({x}\right)\Rightarrow{u}'\left({x}\right)=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{2}^{−{i}} ×\mathrm{2}^{{i}} {x}^{\mathrm{2}^{{i}} −\mathrm{1}} \\ $$$${u}'\left({x}\right)={x}^{−\mathrm{1}} \underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{x}^{\mathrm{2}^{{i}} } ={x}^{−\mathrm{1}} \left({x}^{\mathrm{2}} +{x}^{\mathrm{4}} +{x}^{\mathrm{8}} +{x}^{\mathrm{16}} +…+{x}^{\mathrm{2}^{{n}−\mathrm{1}} } +{x}^{\mathrm{2}^{{n}} } \right) \\ $$$${u}'\left({x}\right)={x}^{−\mathrm{1}} {x}^{\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{6}} +{x}^{\mathrm{12}} +…+{x}^{\mathrm{2}^{{n}−\mathrm{1}} −\mathrm{2}} +{x}^{\mathrm{2}^{{n}} −\mathrm{2}} \right) \\ $$$${u}'\left({x}\right)={x}\left(\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{6}} +{x}^{\mathrm{12}} +…+{x}^{\mathrm{2}^{{n}−\mathrm{1}} −\mathrm{2}} +{x}^{\mathrm{2}^{{n}} −\mathrm{2}} \right) \\ $$$$\left\{{Continue}\right\} \\ $$$$ \\ $$
