Question Number 596 by 123456 last updated on 08/Feb/15
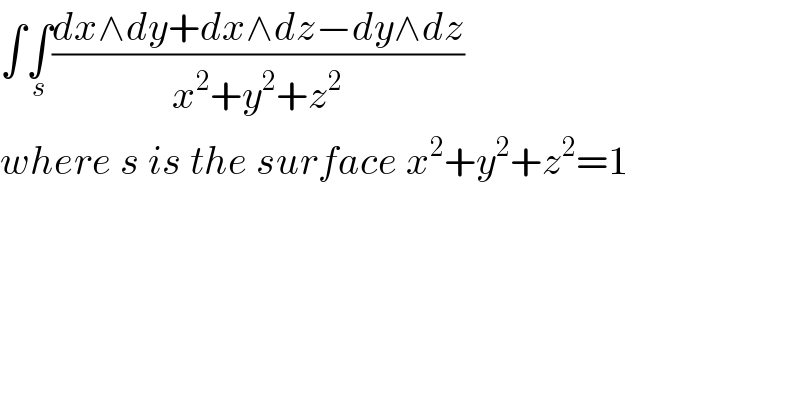
$$\int\underset{{s}} {\int}\frac{{dx}\wedge{dy}+{dx}\wedge{dz}−{dy}\wedge{dz}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} } \\ $$$${where}\:{s}\:{is}\:{the}\:{surface}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} =\mathrm{1}\: \\ $$
